Критерий согласия Пирсона

Критерием согласия называется критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Пусть по выборке объема п получено эмпирическое распределение:

Варианты xi	x1	x2	...	xs
Частоты ni	n1	n2	...	ns

С помощью критерия Пирсона можно проверить гипотезу о различных законах распределения генеральной совокупности (равномерном, нормальном, показательном и др.) Для этого в предположении о конкретном виде распределения вычисляются теоретические частоты , и в качестве критерия выбирается случайная величина

,

имеющая закон распределения χ² с числом степеней свободы k = s – 1 – r, где s – число частичных интервалов выборки, r – число параметров предполагаемого распределения. Критическая область выбирается правосторонней, и граница ее при заданном уровне значимости α 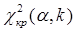находится по таблице критических точек распределения χ².

Теоретические частоты вычисляются для заданного закона распределения как количества элементов выборки, которые должны были попасть в каждый интервал, если бы случайная величина имела выбранный закон распределения, параметры которого совпадают с их точечными оценками по выборке, а именно:

а) для проверки гипотезы о нормальном законе распределения = п ∙ Р_i, где п – объем выборки, x_i и x_{i + 1} – левая и правая границы i-го интервала, - выборочное среднее, s – исправленное среднее квадратическое отклонение. Поскольку нормальное распределение характеризуется двумя параметрами, число степеней свободы k = n – 3;

б) для проверки гипотезы о показательном распределении генеральной совокупности в качестве оценки параметра λ принимается 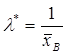. Тогда теоретические частоты = п ∙ Р_i, . Показательное распределение определяется одним параметром, поэтому число степеней свободы k = n – 2;

в) для проверки гипотезы о равномерном распределении генеральной совокупности концы интервала, в котором наблюдались возможные

значения Х, оцениваются по формулам:

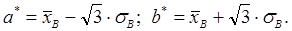
Тогда плотность вероятности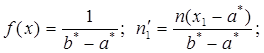

Число степеней свободы k = n – 3, так как равномерное распределение оценивается двумя параметрами.

Практическая часть

Часть I

Задание 1.1

Производится три независимых испытания, в каждом из которых вероятность появления события А равна 0,4. Составить закон распределения дискретной случайной величины X - числа появлений события А в указанных испытаниях. Найти матема-тическое ожидание, дисперсию и среднее квадратическое отклонение X.

Решение:

Для начала построим закон распределения вероятностей для 3-х испытаний:

нам дана p=0,4; q=1-0,4=0,6

A₀{0}=Ᾱ₁*Ᾱ₂*Ᾱ₃=0,6*0,6*0,6=0,216

A₁{1}=A₁* Ᾱ₂*Ᾱ₃+ A₃* Ᾱ₂*Ᾱ₁+ A₂* Ᾱ₁*Ᾱ₃=0,432

A₂{2}=A₁*A₂* Ᾱ₃+ A₁*A₃* Ᾱ₂+ A₂*A₃* Ᾱ₁=0,288

A₃{3}= A₁*A₂*A₃=0,064

x
p	0,216	0,432	0,288	0,064

Теперь можем найти математическое ожидание, дисперсию и среднее квадратичное отклонение:

Математическим ожиданием дискретной случайно величины называют сумму произведений всех её возможных значений на их вероятности:

M(X)=x₁p₁₊x₂p₂+…+x_np_n.

M(X)=0*0,216+1*0,432+2*0,288+3*0,064=1,2

Дисперсией случайной величин называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

D(X)=M[X-M(X)]², однако мы воспользуемся формулой D(X)=M(X²)-[M(X)]²которая быстрее ведет к цели.

M(X²)= 0²*0,216+1²*0,432+2²*0,288+3²*0,064=2,16

D(X)= 2,16-1,2=0,96;

=√D(X);

=

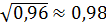
Задание 1.2

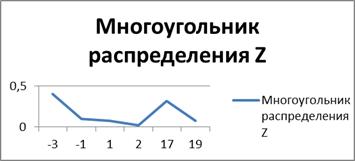
Случайные величины X и Y заданы законами распределений. Определить математическое ожидание, дисперcию и среднее квадратическое отклонение величин X и Y. Составить законы распределения случайных величин Z=X+Y, V=XY. Построить многоугольник распределения случайной величины Z. Найти математическое ожидание и дисперсию случайной величины W=2X-4Y

X
P	0,5	0,1	P3

Y	-6
Q	0,8	0,2

Решение:

Для начала найдем значение P3. ,следует, P3=1-(0,5+0,1); P3=0,4.

M(X)=x₁p₁₊x₂p₂+…+x_np_n.

M(X)=3*0,5+5*0,1+7*0,4=4,8; M(Y)=-6*0,8+14*0,2=-2.

Математическое ожидание нам уже известно, напишем закон распределения для X² и Y²:

X
P	0,5	0,1	0,4

Y
Q	0,8	0,2

M(X²)=9*0,5+25*0,1+49*0,4=26,6;

M(Y²)=36*0,8+196*0,2=68.

Найдем искомые дисперсии применяя формулу D(X)=M(X²)-[M(X)]²:

D(X)=26,6-4,8=21,8;

D(Y)=68+2=70.

Найдем среднеквадратичное отклонение:

=√D(X);

; .

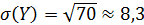Составим законы распределения случайных величин Z=X+Y, V=XY.

Z=X+Y:

Z₁=3-6=3 p₁=0,5*0,8=0,4

Z₂=3+14=17 p₂= 0,5*0,2=0,1

Z₃=5-6=-1 p₃=0,1*0,8=0,08

Z₄=5+14 p₄=0,1*0,2=0,02

Z₅=7-6=1 p₅=0,4*0,8=0,32

Z₆=7+14=21 p₆=0,4*0,2=0,08

Z	-3		-1
P	0,4	0,1	0,08	0,02	0,32	0,08

V=XY:

V₁=-6*3=-18

V₂=-6*5=-30

V₃=-6*7=-42

V₄=14*3=42

V₅=14*5=70

V₆=14*7=98

V	-18	-30	-42
P	0,4	0,1	0,08	0,02	0,32	0,08

Найдем математическое ожидание и дисперсию случайной величины W=2X-4Y:

M(W)=M(2X-4Y)=M(2X)-M(4Y)=2M(X)-4M(Y)=2*(4,8)-4*(-2)=17,6

D(W)=D(2X)+D(-4Y)=4D(X)-16D(Y)=-1032,8.

Задание 1.3

Непрерывная случайная величина задана функцией распределения F(x). Найти:

Вероятность попадания случайной величины Х в интервал (a; b)

Плотность распределения f(x)

математическое ожидание, дисперcию и среднее квадратическое отклонение случайной величины X

построить графики функций F(x), f(x).

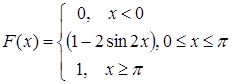
Решение:

P(a<x<b) = F(b)-F(a) или P(a<x<b) = .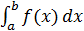

= =

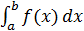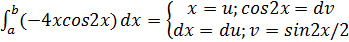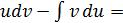
= xcos2x- = =

= = =

= .

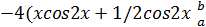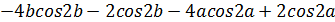M(X) = =

= =

=

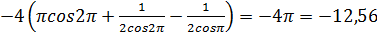
D(X)=

Графики функций

F(X) f(x)

Часть II

Задание 2.1.

По имеющимся данным построить закон распределения заданной случайной величины (см. варианты задания). Необходимо:

1. Построить вариационный (или интервальный) ряд исследуемой случайной величины.

2. Произвести группировку данных вариационного ряда на 6 - 10 интервалов (разрядов, групп), построить таблицу частот, вычислить и представить графически эмпирические функции распределения исследуемой случайной величины.

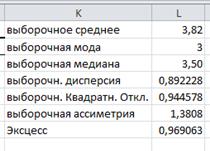
3.Определить основные характеристики выборочной совокупности для исследуемой случайной величины.

4. Построить доверительный интервал для дисперсии заданной случайной величины (выбрать α = 0,05; 0,01; 0,1 самостоятельно).

Вариант №10.

Уровень инфляции (% в месяц): 3.1; 3.7; 6.4; 3.8; 4.2; 3.0; 3.2; 3.7; 3.0; 3.1; 3.6; 4.1; 4.8; 5.5; 3.0; 3.1; 3.2; 3.0; 3.7; 3.5; 3.1; 3.2; 3.0; 3.1; 3.0; 3.4; 3.5; 3.6; 4.1; 3.7; 4.2; 3.8; 4.6; 4.7; 5.1; 5.8; 3.1; 3.0; 5.4; 6.0; 6.2; 3.0; 3.2; 3.4; 3.5; 3.3; 3.3; 3.0; 4.0.

График относительных частот График накопленных частот

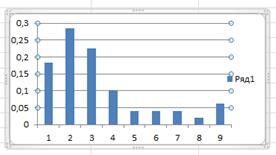
Доверительные интервалы для среднего и дисперсии заданной случайной величины:

Задание 2.2. Проверка статистических гипотез.

Задача1.

По двум выборкам нормальных законов распределения проверить гипотезу о равенстве дисперсий (при конкурирующей гипотезе об их неравенстве) при уровне значимости 0,1.

H₀: (X)= (Y), H₁:D(X)≠D(Y).

Первая выборка: 66.9 50.0 59.1 60.5 59.8 64.2 64.4 52.2 44.2 68.6 61.9 57.2

Вторая выборка: 31.4 25.8 38.3 17.9 51.1 35.1 38.8 46.3 52.4

Решение:

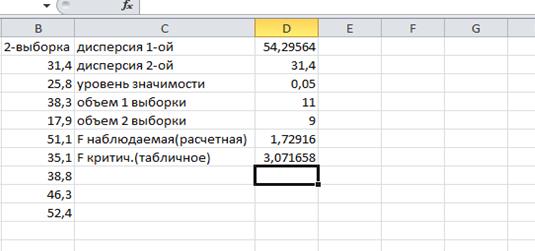
Определим исправленные выборочные дисперсии первой и второй выборок:

S₁=54,29564, S₂=31,4;

Вычислим наблюдаемое значение критерия(отношение большей дисперсии к меньшей):

F_набл=S_Б²/S_М²=54,29564/31,4=1,72916

По условию конкурирующая гипотеза имеет вид H₁:D(X)≠D(Y), поэтому критическая область-двустороняя, значит, что при отыскании критической точки следует брать уровень значимости , вдвое меньший заданного.

По уровню значимости α/2=0,1/2=0,05 и числам степеней свободы κ₁=9-1=8 и κ₂=11-1=10 найдем критическую точку:

F_кр= (0,05;8;10)=3,071658.

На основании полученных данных сделаем вывод о принятии или не принятии гипотезы:

Так как F_набл<F_кр=>H₀, нет основания отвергнуть нулевую гипотезу.

Задача 2.

По данным двух выборок нормального закона распределения проверить гипотезу о равенстве генеральных средних (при конкурирующей гипотезе об их неравенстве) при уровне значимости α.

Решение:

Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу H₀:M(X)=M(Y) о равенстве генеральных средних двух нормальных совокупностей(в случае малых независимых выборок) при конкурирующей гипотезе H₁:M(X)≠M(Y), надо вычислить наблюдаемое значение критерия.

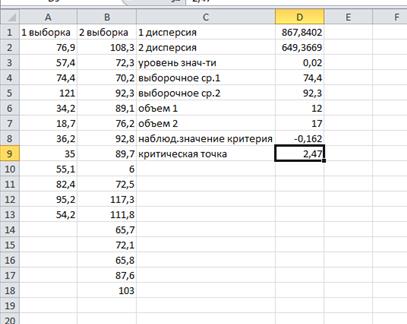
Определим дисперсии первой и второй выборок:

S₁²=867,8402, S₂²=649,3669. Объем выборок n=12,m=17

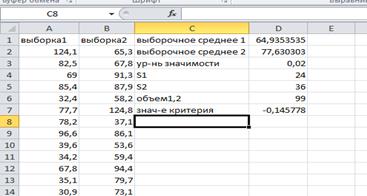
Рассчитаем выборочные средние:

.

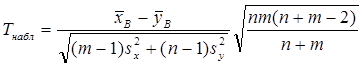
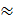-0,162

и по таблице критических точек распределения Стьюдента, по заданному уровню Взначимости α и по числу степеней свободы κ=n+m-2 найти критическую точку t_{двуст.кр}(0,02;27)=2,47.

Так как|T_набл|<t_{двуст.кр}(α;κ) – нет оснований отвергнуть нулевую гипотезу.

Задача 3.

По данным двух выборок нормального закона распределения (первая - с дисперсией S₁², вторая - с дисперсией S₂²) проверить гипотезу о равенстве средних значений при уровне значимости α (при конкурирующей гипотезе об их неравенстве).

Выборка 1:

124.1 82.5 69.0 85.4 32.4 77.7 78.2 96.6 39.6 34.2 67.8 35.1 30.9 69.6 101.0 61.6 115.1 39.2 66.6 92.3 53.0 95.3 55.5 92.2 66.1 57.2 29.5 68.2 40.5 54.0 40.4 72.0 69.2 35.2 98.5 26.9 47.0 106.4 50.2 46.2 88.4 56.6 45.4 69.3 63.5 42.6 66.0 80.1 66.4 92.0 60.9 75.7 109.2 47.1 64.5 93.3 49.4 65.9 98.7 46.2 24.2 50.5 92.4 75.1 112.0 14.6 41.0 59.5 59.7 44.9

108.7 68.8 49.9 44.4 48.2 48.3 87.9 59.5 67.8 62.7 61.5 40.7 68.1 65.1 59.6 77.3 77.0 74.0 99.4 67.2 76.9 99.9 29.0 18.3 56.5 81.8 28.3 66.7 63.1 79.6

Выборка 2:

65.3 67.8 91.3 87.9 58.2 124.8 37.1 86.1 53.6 59.4 94.4 79.7 73.1 18.5 54.7 107.0 78.0 70.2 99.7 117.4 97.0 82.8 68.3 98.3 42.1 76.9 71.2 54.4 98.5 103.8 119.6 47.1 91.8 99.1 90.8 36.4 64.3 72.6 81.1 120.5 79.2 99.4 96.3 77.4 148.4 85.6 92.8 104.3 61.4 83.5 43.1 97.0 111.4 169.8 88.1 52.0 138.4 49.9 79.3 45.2 18.6 108.2 142.9 22.3 79.0 39.9 146.6 76.9 65.4 125.8

27.0 54.4 43.7 88.0 54.7 115.8 66.1 78.8 76.6 55.8 61.8 47.1 80.3 90.9 52.5 16.2 35.0 89.4 30.5 87.0 94.1 73.6 99.2 66.9 62.3 85.8 64.6 96.4 22.0 78.

S₁² = 24, S₂² = 36, α = 0.020

Решение:

Имеются две независимые выборки большого объема, извлеченные из генеральных совокупностей, законы распределения и дисперсии которых неизвестны. При этом для объема выборки, не меньшего 30, можно считать, что выборочные средние распределены приближенно нормально, а выборочные дисперсии являются достаточно хорошими оценками генеральных дисперсий (следовательно, считаем известными приближенные значения генеральных дисперсий):

=64,9353535, 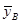=77,630303. Объемы выборок n=99, m=99.

= S₁ = 24

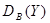= S₂ = 36

Для того чтобы при заданном уровне значимости а проверить нулевую гипотезу Но: М (Х) = М (У) о равенстве математических ожиданий двух нормальных генеральных совокупностей с известными дисперсиями при конкурирующей гипотезе Н₁: М(Х)≠М(У), надо вычислить наблюдаемое значение критерия Z_набл и по таблице функции Лапласа найти критическую точку:

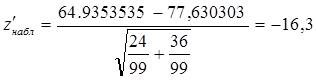
Вид критической области зависит от типа конкурирующей гипотезы:

Н₁: М (Х) ≠ М (Y) – критическая область двусторонняя, z_кр определяется как аргумент функции Лапласа, при котором 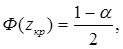и критическая область задается неравенством |Z| > z_кр.

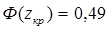z_кр.=0,1879

Так как Z^’_набл <Z_кр опровергаем Н_о (нулевую) гипотезу.

Задача 4.

При проведении n₁ испытаний в первой серии число благоприятных исходов равнялось m₁. Во второй серии из n₂ испытаний число благоприятных исходов равнялось m₂. Проверить гипотезу о равенстве вероятностей благоприятного исхода в двух сериях (при конкурирующей гипотезе об их неравенстве) при уровне значимости α.

Решение:

Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу H₀:p₁=p₂=p о равенстве вероятностей появления события в двух испытаниях при конкурирующей гипотезе H₁:p₁≠p₂, надо вычислить наблюдаемое значение критерия

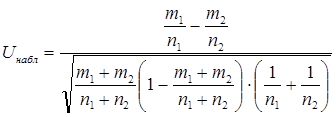
Подставив m₁=496, m₂=576, n₁=700, n₂=800, получим U_набл 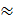-0,011

Найдем критическую точку по равенству

Ф(u_кр)=(1-α)/2=(1-0,03)/2=0,485

По таблице функции Лапласа находим u_кр=2,16.

Так как | U_набл|<u_кр – нет оснований отвергнуть нулевую гипотезу.

5.Задача.

По данным выборки выбрать гипотезу о виде закона распределения и проверить ее, используя критерий Пирсона при уровне значимости α.

Объем выборки п = 100. Вариантами середины частичных интервалов: х₁ = -24,8063, х₂ = -18,4188,…, х₆ = 19,90625.

Найдем = -2,45; σ_В = 15,64612; s = 9,197756.

Вычислим теоретические частоты в предположении о показательном распределении генеральной совокупности при λ*=1/(-2,45)=-0,40816:

= п ∙ Р_i, ;

n₁’=-0,05032, n₂’=-0,68239, … n₈’=337686,8 .

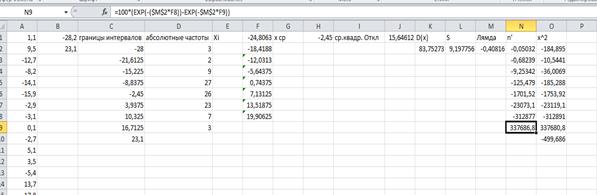
Наблюдаемое значение критерия находим по формуле ,

x²_набл=-499,686. Критическая точка χ²(0,05;6)=12,6; 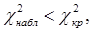следовательно, гипотеза о показательном распределении принимается.

Заключение

В заключение хотелось бы еще раз подчеркнуть, что подавляющее большинство природных и рукотворных явлений, а также явлений повседневной жизни содержат в себе элементы случайности. Окружающий нас мир насыщен случайными событиями: номера выигравших билетов в лотереях, результаты спортивных состязаний, состояние погоды, количество солнечных дней в течение года и так далее.

Знание закономерностей, которым подчиняются случайные явления, позволяет предвидеть, как эти явления будут протекать. Теория вероятностей не ставит перед собой задачу предсказать, произойдет или не произойдет некоторое событие. Однако если данное событие многократно наблюдается (или повторяется), то оно подчиняется определенным закономерностям, а именно вероятностным закономерностям. Установлением этих закономерностей и занимается теория вероятностей.

Итак, в теории вероятностей изучаются реально существующие независимо от нашего сознания законы случайных явлений. Теория вероятностей предлагает математический аппарат для описания этих законов.

Список литературы

Гмурман В.Е. «Теория вероятностей и математическая статистика»

Вентцель Е.С. «Теория вероятностей»

Колемаев В.А. «Теория вероятностей в примерах и задачах»

Агапов Г.И. «Задачник по теории вероятностей»

Гмурман В.Е «Руководство к решению задач по теории вероятностей и математической статистике»