Метод замены переменной в пределе
Весьма ходовой приём решения. Метод замены переменной применяют чаще всего для того, чтобы свести решение к первому замечательному пределу, намного реже – к другому замечательному пределу. Рассмотрим пару типовых образцов:
Пример 14
Найти предел

Решаем:

В пределе находится арктангенс, от которого хорошо бы избавиться. Логично и очень удобно превратить «арк» в одну единственную букву. Проведём замену переменной:  .
.
Теперь в пределе нужно выразить всё остальное через «тэ».
Во-первых, выясним, куда будет стремиться новая переменная «тэ»:
Если  , то
, то 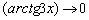 , иными словами, новоиспеченная переменная тоже будет стремиться к нулю:
, иными словами, новоиспеченная переменная тоже будет стремиться к нулю: 
Осталось в знаменателе выразить «икс» через «тэ». Для этого на обе части равенства  «навешиваем» тангенсы:
«навешиваем» тангенсы:
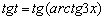
В правой части две взаимно обратные функции уничтожаются:
 , откуда:
, откуда: 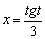
Взмахи волшебной палочки закончены, остальное просто:
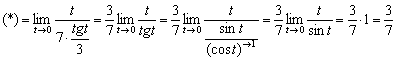
Используемые формулы и приёмы решения завершающего этапа очень подробно разобраны в первой части урока Замечательные пределы.
Пример 15
Найти предел
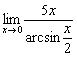
Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.
Ещё пара занятных примеров на тему замены переменной:
Пример 16
Найти предел

При подстановке единицы в предел получается неопределённость 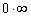 . Замена переменной уже напрашивается, но сначала преобразуем тангенс по формуле
. Замена переменной уже напрашивается, но сначала преобразуем тангенс по формуле 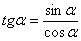 . Действительно, зачем нам тангенс?
. Действительно, зачем нам тангенс?

Заметьте, что  , поэтому
, поэтому 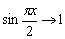 . Если не совсем понятно, посмотрите значения синуса втригонометрической таблице. Таким образом, мы сразу избавляемся от множителя
. Если не совсем понятно, посмотрите значения синуса втригонометрической таблице. Таким образом, мы сразу избавляемся от множителя 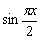 , кроме того, получаем более привычную неопределённость 0:0. Хорошо бы ещё и предел у нас стремился к нулю.
, кроме того, получаем более привычную неопределённость 0:0. Хорошо бы ещё и предел у нас стремился к нулю.
Проведем замену: 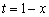
Если 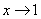 , то
, то 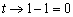
Под косинусом у нас находится «икс», который тоже необходимо выразить через «тэ».
Из замены 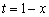 выражаем:
выражаем:  .
.
Завершаем решение:
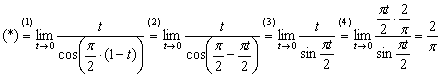
(1) Проводим подстановку
(2) Раскрываем скобки под косинусом.
(3) Используем формулу приведения 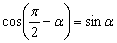 , формулы приведения также можно найти в тригонометрических таблицах.
, формулы приведения также можно найти в тригонометрических таблицах.
(4) Чтобы организовать первый замечательный предел  , искусственно домножаем числитель на
, искусственно домножаем числитель на 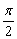 и обратное число
и обратное число 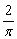 .
.
Задание для самостоятельного решения:
Пример 17
Найти предел

Полное решение и ответ в конце урока.
Это были несложные задачи в своём классе, на практике всё бывает хуже, и, помимо формул приведения, приходится использовать самые разные тригонометрические формулы, а также прочие ухищрения. В статье Сложные пределы я разобрал пару настоящих примеров =)
В канун праздника окончательно проясним ситуацию ещё с одной распространённой неопределённостью:
