StWd, COSlf ', - COS* ; - StHcisitHf 4 страница

, Ctfl<* COS^-tgA.5VHtf-tgA_iSVH>f_t-ctgal._<C03y₁

3 tgAcosvf-toA^osip+ ctooisiKtp+ctQ<i,₁siHif₁

Анализируя рассмотренные примеры систем статических углов, приходим к следующим выводам.

1. Приведенные выше системы сформировались на основе потреб­ностей улучшения условий процесса резания, а также упрощения тех­нологий производства режущих инструментов.

2. Различие систем базируется прежде всего на том, сочетанием каких отрезков прямых, представляющих собой линии пересечения со­ответствующих рабочих и секущих плоскостей, задается положение

в пространстве трех рабочих поверхностей резца: передней, главной и вспомогательной задней.

3. Необходимость классификации систем углов отпадет в условиях
математического описания положения в пространстве рабочей части
режущих инструментов. Переход к математическому описанию (зада­
нию) наиболее просто осуществить на основе метода прямоугольных
координат — основного метода геометрического исследования материа­
льных тел, разработанного в аналитической геометрии. При этом именно
статические углы инструмента и направляющие косинусы этих углов мо­
гут составить те конкретные данные, без знания которых невозможно
установить координаты режущих кромок, отрезков прямых и плоскостей.

2.3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ПОЛОЖЕНИЯ РЕЖУЩИХ КРОМОК И РАБОЧИХ ПОВЕРХНОСТЕЙ В СТАТИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ 2.3.1. Исходное положение статической системы координат В общем случае некоторая прямоугольная система координат ^2 ^-^относительно режущего Инструмента может быть выбрана весь­ма произвольно. Однако только в статической системе координат Xw УуХу режущего инструмента, одна из осей которой совпадает с вектором скорости главного движения, в качестве направляющих уг­лов могут быть использованы статические углы, измерять которые можно с высокой степенью точности.

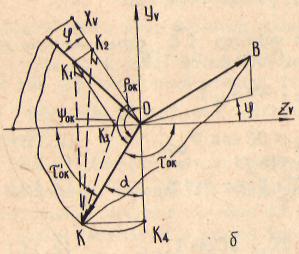
Рассмотрим метод построения базовой системы координат ^ У Z_v на примере токарной обработки (рис. 2.10). Центром системы выбе­рем точку, расположенную на вершине редца. Линию, проходящую че­рез вектор скорости главного движения V , принимаем за ось Уу . Она параллельна оси станка У . Положение двух других осей находим методом проведения из вершин резца линий, параллельных координат­ным осям X и Z„ станка. На этом построение искомой системы ко-

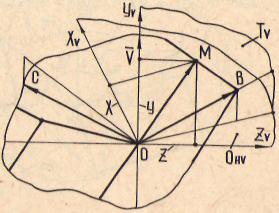ординат практически закончено. Остается обозначить оси полученной системы координат и задать им положительное направление. В качес­тве примера обозначения осей координат и выбора их направления ос­тановимся на варианте обработки проходным резцом (рис. 2.10,2.11).

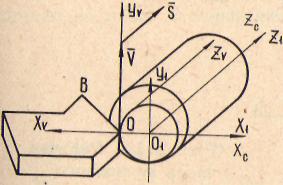
Рис. 2.10. Схема токарной обработки проходным резцом

Рис. 2.11. Схема расположения базовой системы координат

12.3.2. Методика определения координат режущих кромок и отрезков прямых, лежащих на рабочих поверхностях режущего инструмента В результата построения режущие кромки и рабочие поверхности ца оказались расположенными в системе координат ХуУуЯу .Для еделения их положения используем метод условного проведения режущих кромках и рабочих поверхностях режущего инструмента личных векторов с последующим заданием их положения в системе координат с помощью направляющих косинусов. Тогда положение в пространстве режущей кромки можно будет определять координатами ■диого расположенного на ней единичного вектора. Рабочие же поверх— п.. ги можно будет описывать координатами двух-трех лежащих на нич единичных векторов.

2.3.2.1. Координаты единичных векторов, расположенных на осях координат

Если точка М (рис. 2.12), лежащая на оси Zy , имеет коорди-
"'4.1 М ( 0 i 0 , Z )i го отрезок (вектор) ОМ будет иметь следу-
...... не координаты:

0M=(0-X_o; a-v, Z-Z_o)=(0; 0;Z),

где X₀, Я₀ , Z₀ - координаты точки 0 . Так как^точка 0 - начало координат, то Х-=0; 9₀=0; Z₀=O. Если отрезок ОМ равен единичному вектору К, то к ⁼ (°» О; 1).

2.3.2.3. Координаты единичных векторов, лежащих на режущих кромках инструмента

Определим координаты^единичного вектора, лежащего на главной режущей кромке. Пусть О В - единичный вектор, лежащий на глав­ной режущей кромке (рис. 2.13,а). Из рис. 2.13, а имеем:

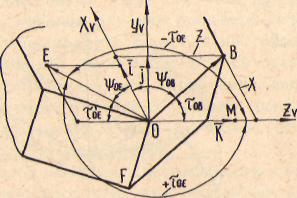Рис. 2.12. Рабочая часть проходного резца

По аналогии'с_ К , для единичных векторов г и j .лежащих на осях X_v иУ_у, имеем i= (1; О; О); f- ( О; 1; О).

2.3.2.2. Координаты единичных векторов, лежащих на координатных плоскостях

Пусть единичный вектор О В лежит на плоскости Ху OZy(рис. 2.12).Точка В имеет координаты X , 0 , Z . Обозначим направля­ющие углы вектора О В через Т|Г и К _oft . Тогда из рис. 2.12 имеем: X = C0s'4'₀-; Z=C0St„.Следовательно,

0B=tX-0-,0;Z-0)=(cosV_0Bl0;co»T!_0BV

Подобным же образом для единичного вектора О Е , лежащего во второй четверти системы координат Ху OZy. получаем:

б!=(+Х; 0;-Z) =(cosV_0E \ 0;cos<c_OE)=(cosV_OE';0;-co_S^_E).

В дальнейшем направляющие углы между вектором и осью коорди­нат X будем обозначать через W ( W ); между вектором и осью У — через J» ( р ) и соответственно через <ь ( "С") - углы, лежащие между осью Z и вектором. Для выделения положительных и отрица­тельных значений углов примем следующее правило.

Положительными углами, как это принято в курсе высшей матема тики, будем считать те углы, отсчет которых производится против ча совой стрелки, если смотреть со стороны отрицательного направления оси координат, перпендикулярной к плоскости отсчета. На рис. 2.12 е качестве примера показаны положительное и отрицательное значен

'ОЕ '

0B = Ccos4r,

06 1

^С05Лв;^С05(С «пр-

опустим из точки В перпендикуляры на плоскость Ху 0Z_V и ось Z_v

Dj -I О

Рис. 2.13.Схема расположения единичного вектора на режущих кромках: а - главной; б — вспомогательной

ассмотрим образовавшуюся пирамиду 0ВВ,,в_:

дОВВ.

0В₁= 0 В cos А,

(2.1)

Д 0В,В₂-~ОВ_г=0В₂/cos ^; дОВВ_г^о_В OB cost

Об'

Решив зависимости (2.1), получаем:

cos<C₀ = cosA,cos<f. (2.2)

Опустим перпендикуляр из точки В на ось X_v . Рассмотрим пи­рамиду D В В, К :

д О В В,-* OB, = О В cos X;

д 0ВК-»0К = 0В,51ч(р; _(2>3)

д О В К-*- OK = 0BcosY_OB.

(2.4)

Из зависимости (2.3) получаем:

cosV= cosAsinip.Определим значение cosP₀«. Из рис. 2.13,а имеем:

j»_oe= 90°-Л/;cosj9_0B=cosC90"-Jl) = sinX. (2.5)

В итоге координаты единичного вектора О В , лежащего на главной режущей кромке, будут следующими:

0&= (.^c°sA,3tKcp; stnA; eosA cosip).(2.6)

Рассмотрим другой метод решения. Из рис. 2.13, а имеем:

б1=(х,у,х)=(ок;ом; ов_г).

Так как ОВ единичный вектор, то ОМ= cos(90°- Х)в sinA;

0B,=cosA.,' OB = 0B.cos<f = cosXcosif; 0K= 0B,simp = cosXsin<p.

В итоге

OB^e(cosXei.rttf, s-ihA^cosA, cosw).Определим координаты единичного вектора Oil, лежащего на вспо­могательной режущей кромке: ОБ =Ссов"НС_'.,^cos^оз>» '"^ол^ ' ^^{3 точки} Б вспомогательной режущей кромки опустим перпендикуляр на ось Z и плоскость X_v0Z_v(pnc. 2.13,6). Рассмотрим пирамиду OBI,D. :

д0В2₁->.0В = 0В₁/со8Л₁;
aOD^-OD^QBj/coshv (2.7)

д01П)_г-*01}₂ = ODcost'pj,; cos-c'_a|= cos A,, cos(f_r

В итоге получаем:

cost;

=-cost' ; cost._ =-cosif,cosД,.- (2.8)

AT) ' OD

Определим cosB_n-. Из рис. 2.13,6 имеем:

ja_0I= 90°+ A,, ;cos_>p_OIl=cos(fl0⁰₊A₁)=-siKJl₁.⁽²-⁹⁾ Опустим перпендикуляр из точки I на ось Ху . Рассмотрим пира­миду QD^jD:

д 0JDD,-* ОБ= OBi/cos^; д 0DI₃-* °^з^{= 0Ilcos4,}0B i

дОБ,Б₃- 0Б₃= OB,cos(90°-«р,).(2.10)

Витоге cosY_0B= cos A, sintf^. _^ (1.11)

Таким образом, координаты единичного веь.ора ОБ , лежащего на вспомогательной режущей кромке, будут следующими:

bj = (cosA,₁sih.ip₁;-s{,HA₁;-cosA₁cos«f>_l).

Воспользуемся другим методом решения. Из рис. 2.13,6 имеем:

_ o5 = (x-,-9;-Z)=(oj₃;-oi)₁;-oii₂).

Так как ОВ - единичный вектор, то

OJ^cosA,; 01j= OD^iK^scosA^siHift; QB₂= Oncost?, = cosAiCostp,; ГБ,= sinA,;

ОБ = (cosA^inip, j- tinX_i'₁-coaX₁cos<f_i)•

2.3.2.4. Координаты векторов, лежащих на рабочих поверхностях режущего инструмента

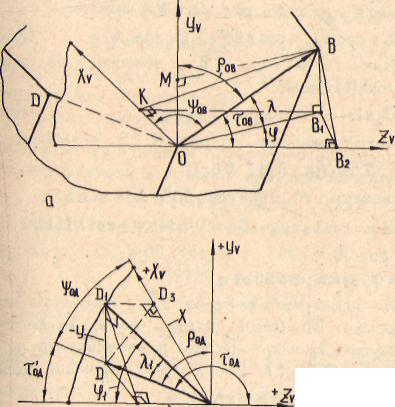
Определим координаты единичного вектора О С , лежащего на пе­редней поверхности в главной секущей плоскости (рис. 2.14,а):

(2.12) (2.13) (2.14)

6c = (co_SV_oc;co_SjD_oc;co_St_oc). Из ОСС, С₂ (рис. 2.14,а) имеем: ОС = 00,/cosг; 0С_г=0С, соэ tp ; 0С_г = ОС cos Y_0o;

⁰ "s^oc ^{= COSi}f ^cos f'

cosJ»_oc= cos(90°+ y)=- sitty.

Из 0СС,С₃следует:

(2.15) (2.16) (2.17)

0C₃=0C,cos(9O-<p); 0C=0C,/cosj; 0C₃= OCcosT^;

cosX^.= cosysi*<p ; cosi;_oc=-costj_C; cosZ^-cosfsiny.
II итоге _^

OC = (cosip.cosj ;-stH,t" ;-cosy si№<f)-

Имеется второй вариант решения. Если считать вектор ОС, единич­ным, то₍ гак как он лежит в плоскости X_v OZy, его координатами будут (рис. 2.14,а): _^

ОС, = (cosip \ 0 '■,- sin if). По вектор ОС) является проекцией единичного вектора ОС> поэто-My[OC,|=cosy и 00,= (cosycosip; 0;-cosy sirtip) . В результате

0С = ОС, + СС, = (cosy cosif ;-sin.v;-simpccsy), где C^=(0',-siHy; 0)

с, yaor-i о

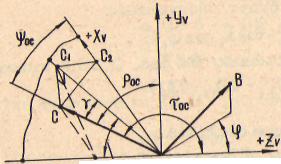
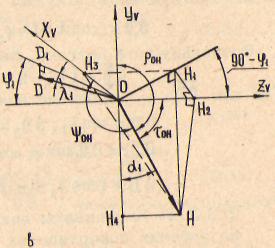
Рис. 2.14. Схема

расположения единичного

вектора на поверхностях:

а - передней;

б — главной задней;

в - вспомогательной

задней

(2.18) (2.19) (2.20)

При Т ⁼ ^1 i fi ⁼ 90 — if вектор О С становится некоторым векто­ром Ос' , лежащим на вспомогательной режущей кромке: ОС = 0D*(cosX₁5itnf J-svitl,;-cosA,cosif,). Определим координаты единичного вектора, лежащего на главной задней поверхности в главной секущей плоскости (рис. 2.14,6). Та­ким единичным вектором является вектор О К . Спроектируем его на плоскость Xy0Z_v . Из фигуры ОКК,К, имеем:

0К_г=ОК,со5ц>' О К, = ОК.cos (.90^е-.1); 0К_г = OK cosY_ol<; cosY_0K = cosif.svtt,oi.-, ₍Р_0К = 180-сс;

^cosPoK=^{_ cos}«*-Из фигуры ОК,К,К следует: OKj= OK^cos 130^е-ifV,

OK^OKcOSlSC-ot); ОК₃=ОКС05Т;„_К', COST'= Stasia if ; (2.21)

(2.22) (2.23)

cos'C_0K=- COSir_0K=-Sirt<*SvH,tf;

OK =(cosip siivoi-;-cos«i.;-siito(,simp). Рассмотрим более простой вариант решения: 0К = Ь\+ ol^tOKj',-0^;- 0K₃);0K=strtoc;0K₂=sittAcos₄-;flK_J-si»t«isk(p;0K^cos<t.

После подстановки получаем

OK = (si№ctc03lf )-COS<i;-si(lcl Siltlf).Рассмотрим координаты единичного вектора СГн , лежащего во вспомогательной секущей плоскости (рис. 2.14,в). Единичные векто­ры 03] и ОН лежат на вспомогательной задней поверхности, ОН. -проекция ОН на плоскость X_v0Zy . Из фигуры

оннгнг

(2.24) (2.25) (2.26)

0Н_г= ОН, cos С 90^е-ip,); 0Н,= ОН skd; 0Н_г=0Нсозт;_он}

cosjd_oh= cos с180°-сц)=-C0Sd_v

Из фигуры

ОН = O^cosip; 0Н;= OHstwi; 0Н3= 0HcosY0H-

(2.27)

онн,н₃-*

В итоге

cosY_OH=siito^cosi^;

(2.28)

OHstcosi^siturt, ;-cosot₁;st(tot₁sittif₁). (2.29)

Приведем упрощенный вариант решения. Из рис. 2.14,в имеем:

_ 0H = 0H₁+0H^ = (+X;-9; + z)=(0H₃;-0H₄; 0Н_г);

0H, = sirt,o^; OHjsSlHdiCOS^; OH^siud^siKifi; OH^cosd,;

0H = (ein.<i₁COSlf₁^-_?- COSot, ; sinij^ SV.Hcl,).

2.3.3. Вывод уравнений , определяющих положение рабочих поверхностей, координатных и секущих плоскостей

Выведем уравнение передней поверхности. Упрощенно считаем ее плоскостью, проходящей через главную режущую кромку и линию пе­ресечения передней поверхности с главной секущей плоскостью, т.е. через векторы 08 и ОС (см. рис. 2.11):

0В = (cosX siittfy stn-A. J cos Л cos if);

= 0;

ОС « (cosif cosy • - siny;-cosy sitiif). Уравнение передней поверхности - плоскости, проходящей через векторы О В , ОС , и произвольно взятый лежащий на этой плос­кости вектор ОМ - ( X У , Z ) ' найдем с помощью определителя третьего порядка:

cosAsitvif;	svkX ',	cosA. cosip
cos if cos v;	- «it* J!	-cosy simp
X	л	Z

-cueist tt if stnvZ + У cosif eosycosA cos if- XsinA, cosy stttip + + !)cosAstKif cosYsittif- Zcostpcosy siwl + XsiHrcosX cosip= 0.

Окончательное уравнение передней поверхности имеет вид:

X(taycosvf-toAsttvif)+ У-Z. (tor stnif+ talcosip)=:0- (²'³°) Принимая, что taf=taX/tar , получаем:

Xcos(if-f)+ ycbycosf-ZstnCip+fJsO. Найдем уравнение главной задней поверхности, проходящей через О В и линию пересечения главной задней поверхности главной секу­щей плоскостью, т.е. через OK = (stwotcosif^- cosot;-3tnd, stn,^p)j

cosAsvnif, sin A; cosA cosif

= 0.

(2.31)

StWd, COSlf ', - COS* ; - StHcisitHf

Z.

Принимая taQ^taX/сЫк., имеем:

Xcos (.if+9)+ ytgd-cosQ- Zsin (if + Q).Определим уравнение вспомогательной задней поверхности, прохо­дящей через ОБ и линию пересечения вспомогательной задней по­верхности со вспомогательной секущей плоскостью, т.е. через еди­ничный вектор ОН:

0H»(cosif₁ sitiot^-cosd,,', stud, simp,,).
cosA^inip,; -sinl,; -cos^cos^
cosif, sind,.,; - cosoc,; since, sinip,

* 0

X (tqlfSiittp,+ eta*, cosip,) + у +Z CfetgX₁sin.f₁-tqX₁cos<p₁) = 0. Считая, что tgA^geCjs toe , получаем:

^♦.^♦гЙЭс!)'; (2.32)

cose а ' cose

Рассмотрим метод составления уравнений плоскостей, перпендику­лярных к вектору - отрезку прямой. Составим уравнение главной се­кущей^ плоскости, т.е. плоскости, перпендикулярной к проекции векто­ра 0В на плоскость Ху OZy •

Проекция единичного вектора 0 В (см. рис. 2.13_^ лежащего на главной режущей кромке, на плоскость Ху02у(т.е. 0B/X_v0Z_v) равна "ектору 0В, . Из (2.13,а) имеем:

0B/X_v 0Z_V = OB^tcosAsihtp; 0 ; cosl cosip);

— | OB, | = cosA.

Если 0B₁ является единичным вектором, то

OB, = (sinif; 0 ; cos if). Плоскость, перпендикулярная к OB, и проходящая через точку М₀(Х₀^У jZ.), определяется уравнением:

aCX-X₀)₊e(y-9₀) + c(Z-Z_Q) = 0,

где a , в , с - координаты векг_ора, нормального к искомой плоскос­ти (в данном случае вектора 0 В, ); X_fl , У₀ . Z ₀ - координаты точки, 'юрез которую проходит плоскость.

Пусть главная секущая плоскость проходит через точку В, (sitiif' Ojcosif). Тогда уравнение плоскости имеет вид:

sinif (.Х- svttif)+ cos if (Z.-cos if )= 0; Xsinif +Z cos<f-t = 0. (2.33)

Если эта плоскость проходит через начало координат - точку 0(0; 0', 0 ) , то уравнение плоскости упрощается:

si.tnf(X-0) + cosif (JZ-0)=0; Xsinif + Zcostf =0. (2.34)

Составим уравнение плоскости, перпендикулярной к главной режу-ой кромке. Пусть плоскость проходит через точку В (см. рис. 2.13)

Ее координатами являются:

^Btcos Н*ов^{; cos}.?oe 1 ^C0S<C0B^^{= В tc0sJl} slue; sin A- • cosAcos(p). Уравнение плоскости, перпендикулярной к OB , имеет вид:

где ( а ; б ; с ) = (cosY^^tos^; costgg ) _ координаты нормального к искомой плоскости вектора ОВ ; X ₀ • S. i Z_e - координаты точки В . После подстановки получаем:

XcosAsini? + 9si/nA< + cosXcos»pZ=H;(2.35)

Xsinif + tgA,9 + eosifZ^'l/cosA.. Если плоскость, перпендикулярная к OB , проходит через начало координат, то ее уравнение приобретает вид:

Xsintft ЦЦХ +Хсозч = 0. (2.36)

Составим уравнение вспомогательной секущей плоскости, т.е. плос­
кости, перпендикулярной к проекции вспомогательной режущей кромки
на основную плоскость XyOZy . Пусть на рис. 2.13,6 0Б₁ - единич­
ный вектор, лежащий на проекции вспомогательной режущей кромки
на плоскость XyOZy. _^

Й, (sin^ ; 0Jr. cos ip,)j Зц«(»(л.^; Oj-cos?,). Плоскость, перпендикулярная к 0D₁ , проходящая через Л₁ ,имеет

вид:

aU-X₀) + 6(9-9₀HcU-Z₀)=0;

sitv^CX-sin^^ + O+tcosvp^Z + cos^^O;(2.37) Xsin^-Zcos^ - 1 =0.

Если вспомогательная секущая плоскость проходит через, начало координат, то ее уравнением является следующее :

Xsitv^- Z,cos^=.0. ⁽²-³⁸⁾

По аналогии с уравнениями(2;35) и(2,36) плоскость, перпенди­
кулярная к вспомогательной режущей кромке,описывается выражениям
X si tup - Щ§ -Zcos «р,а 1/coei,; (2.39)

xein^-atg^-Zcos^eO. ⁽²-⁴⁰⁾

Уравнение (2.39) справедливо для случая прохождения плоскостичерез точку J, а(2.40) - через начало координат(см.рис. 2.13,6)

Рассмотримпример. В плоскости А, перпендикулярной кпроекции единичноговектора 0D наплоскость XyOZy . лежит единичныйвек*. гор ой ( см. рис. 2.14,в). Определим его координаты с помощью

Г, Л

Мненияплоскости А.

Решение. _» .

OJ^cos^SiKcp }- sinX,; - cosl^ostft);

OB^cosl^slivift; O^-cosA, cos<f,).

Уравнение плоскости A , перпендикулярной к 0Б₁ , проходящей че-Ite начало координат:

XcosA^sinip -Zcos^cos^ = 0.

Мишей пересечения этой плоскости и XyOZyявдяегся QH^ (Xj Oj Z)в (cosA.COSif. '.0', cosX. Svnif.). Искомый вектор QHлежит вплоскости, ■ рш'ндикулярной к ОБ.. Он будет единичным в^том случае, если ОН'+ ОН/]= \ (где ОН'есть часть вектора 0Н₁). Так как |0Н/| = cosd ■ ^т0 j О И * I должно быть равно sii-vol,.Это возможно получить, ни координаты вектора ОН.умножить на sind|/cosA.Bитоге получаем:

ОН'- (sinoL^osip,; 0; slKot^inif,).

il да _».-*.-»•

ОН = ОН' +■ ОН.= (cosvf sinot^-cosot,'siivaCjSitnf,).

Рассмотренные здесь методы составления уравнений рабочих поверх— к гей, базовых и секущих поверхностей могут быть применены для '" iro режущего инструмента.

2.3.4. Методика определения углов между режущими кромками и осями координат, координатными плоскостями

Зная координаты единичных векторов, лежащих на режущих кромках, i 1ЖНО определить углы между режущими кромками и различными ли-1ИЯМИ,плоскостями.

I (пределим угол между главной режущей кромкой и осью Уу (см. ш . 2.13). Единичные векторы, лежащие на оси Уу и главной режу-||' il кромке, имеют следующие координаты:

0В= (cos A, simp; sinl; cos A, cos f); j= (0; 1; 0).

Угол между этими двумя векторами определим по зависимости

10:

12.^* 12. 1 ** 2.

sin, X

Ц^\^;щщ^г

cos

llcos^sin^p + si к.2 А + cos*A cos4p COS 8 = cos (.90°-А,), откуда а = 90°- X.

1 )пределим угол между проекциями главной и вспомогагельной режу— их кромок на пло:кость XyOZy (см.рис. 2.13):

_;= si к Л.;

пределим линию пересечения главной

0B, = (situp; 0", cosif); Sl^aCsift^' 0;-cosif,);

Sinip sittip -cosipcostp.

Y

COS 9 =

sin\ + cos²ip ys«-«²'» J-"¹*¹'

: sin If sin if ~ cos ip COS If = - COS (If +tp.)-

2.4. АНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ УГЛОВ

МЕЖДУ ЛИНИЯМИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ

СЕКУЩЕЙ ПЛОСКОСТЬЮ

Методику решения подобных задач рассмотрим на примерах опреде­ления углов между одной из координатных плоскостей статической си­стемы координат X_vy_vZy и одной из рабочих поверхностей инструмента в сечении третьей плоскостью (например, главной, вспомогательной, продольной или какой-нибудь другой секущей плоскостью).

2.4.1. Углы в главной и вспомогательной секущих плоскостях Определим угол между передней поверхностью резца (см.рис. 2.11) X(tajpcos(f-tolsi.Kip)+ У -Z.(tqj svnip + toXcos *f) = О и плоскостью XyOZy в сечении главной секущей плоскостью X sin^p t Z cos if = 0 . Найдем линию пересечения главной секущей плоскости с передней поверхностью:

t

X sintf +• Zcos ip =0 ; X(tcgcosip - ttj A.sinif)+ y-Z(tg3fsin<f+tgA,cos<p)=0. Уравнения линии пересечения в каноническом виде будут,следующим!

X - X

Z - Z,

У о

о_____

V — V

COS if

SVHlf

COS if

Jtayjitvi ) \+t|^C0Stf /

sinip

/tgjfHnvpA /tjfcosiM \ t|Xcos*f ) ^tjjAsinip/

tolsiaif /

X- x( -cos If

Si n tf

+ t

У -У,

И

В итоге координаты, линии пересечения оказываются равными ЛП₁₌ (-cosip; + tay; + sinsj>).

ю Хк 0ZV

секущей плоскости с плос—

X simp + Z cos ip _s 0, У =0.

равнения линии

_	z - Z 0
	sin if 0 0 1

cos if 0

пересечения в канонической форме:
Х- Х„ Я - Чо_

Svn<f о

COS vf

О

У- У₀

cos ч>

S itv ip

Координаты линии пересечения последних двух плоскостей Л П, -
- (-cosif; 0 ; siw if) . Теперь найдем угол между двумя линиями Пересе—
... ми трех плоскостей (между ЛП₍ и Л П.):

1 п 2 cos ч> t Оч-sJH ф

0056,=:

cos ч> t u + sm ц>_____ 1 1

a : I COS'J-

Таким образом, как и следовало ожидать, искомый угол оказался

в

ШИЫм главному переднему углу г , что полностью совпадает с опре-m IIнем угла V .

¹ ледувг отметить, что правильность положения линии пересечения I и. томе координат можно оценивать с помощью знаков, стоящих пе-^ I и координатами линий пересечения. При необходимости перевода ли-"н пересечения в противоположную четверть системы координат зна— и Перед координатами линии пересечения необходимо поменять на об— • I in.li!. Этого же результата можно достигнуть перестановкой строк ^[|ИИ|вменагеяе канонического уравнения.

Определим угол между главной задней поверхностью и плоскостью

f

QZy в сечении главной секущей плоскостью (см. рис. 2.14,6). иные данные: «) главная секущая плоскость

XstHip +Zcos f = 0;

fl) главная задняя поверхность

XUtoAeosif-toAsiHipJ+y- Z(ctQqtsiH^+tgXcostp)=0^ ill плоскость y_v0Zy ; X - О .