ДЕ8.Теория вероятности
Тема: Числовые характеристики случайных величин
Дискретная случайная величина X задана законом распределения вероятностей:  Тогда ее среднее квадратическое отклонение равно …
Тогда ее среднее квадратическое отклонение равно …  0,80
0,80
Решение:
Среднее квадратическое отклонение случайной величины Х определяется как  , где дисперсию дискретной случайной величины можно вычислить по формуле
, где дисперсию дискретной случайной величины можно вычислить по формуле  .Тогда
.Тогда  , а
, а 
Тема: Определение вероятности
В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет годных, равна …
 | 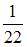 |
Тема: Полная вероятность. Формулы Байеса
В первой урне 5 черных и 6 белых шаров. Во второй урне 3 белых шара и 6 черных шаров. Из первой урны переложили один шар во вторую урну. Тогда вероятность того, что шар, вынутый наудачу из второй урны, будет черным, равна …
 | 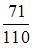 |
Решение:
Для вычисления вероятности события A (вынутый наудачу шар – черный) применим формулу полной вероятности:  .Здесь
.Здесь 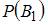 вероятность того, что из первой урны переложили во вторую урну белый шар;
вероятность того, что из первой урны переложили во вторую урну белый шар;  – вероятность того, что из первой урны переложили во вторую урну черный шар;
– вероятность того, что из первой урны переложили во вторую урну черный шар;  – условная вероятность того, что вынутый шар черный, если из первой урны во вторую был переложен белый шар;
– условная вероятность того, что вынутый шар черный, если из первой урны во вторую был переложен белый шар;  – условная вероятность того, что вынутый шар черный, если из первой урны во вторую был переложен черный шар.
– условная вероятность того, что вынутый шар черный, если из первой урны во вторую был переложен черный шар.

Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина Х задана законом распределения вероятностей:  Тогда вероятность
Тогда вероятность 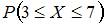 равна …
равна …
 | 0,8 |
Решение: 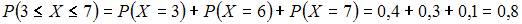
Тема: Числовые характеристики случайных величин
Дисперсия дискретной случайной величины Х, заданной законом распределения вероятностей:  равна 0,06. Тогда значение
равна 0,06. Тогда значение 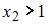 равно …
равно …
 | 1,5 |
Решение:
Дисперсию дискретной случайной величины можно вычислить по формуле  . Тогда
. Тогда
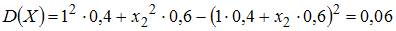 или
или 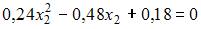 . Решив последнее уравнение, получаем два корня
. Решив последнее уравнение, получаем два корня 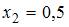 и
и 
Тема: Определение вероятности
В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет годных, равна …
 | 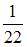 |
Решение:
Для вычисления события А (среди отобранных деталей нет годных) воспользуемся формулой  где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события А. нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно извлечь три детали из 12 имеющих, то есть
где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события А. нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно извлечь три детали из 12 имеющих, то есть 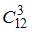 .
.
А общее число благоприятствующих исходов равно числу способов, которыми можно извлечь три бракованные детали из пяти, то есть 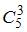 .
. 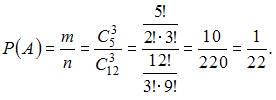
Тема: Полная вероятность. Формулы Байеса
Банк выдает 44% всех кредитов юридическим лицам, а 56% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,2; а для физического лица эта вероятность составляет 0,1. Тогда вероятность того, что очередной кредит будет погашен в срок, равна …
 | 0,856 |
Решение:
Для вычисления вероятности события A (выданный кредит будет погашен в срок) применим формулу полной вероятности:  . Здесь
. Здесь 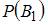 – вероятность того, что кредит был выдан юридическому лицу;
– вероятность того, что кредит был выдан юридическому лицу;  – вероятность того, что кредит был выдан физическому лицу;
– вероятность того, что кредит был выдан физическому лицу;  – условная вероятность того, что кредит будет погашен в срок, если он был выдан юридическому лицу;
– условная вероятность того, что кредит будет погашен в срок, если он был выдан юридическому лицу;  – условная вероятность того, что кредит будет погашен в срок, если он был выдан физическому лицу. Тогда
– условная вероятность того, что кредит будет погашен в срок, если он был выдан физическому лицу. Тогда 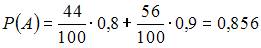
Тема: Законы распределения вероятностей дискретных случайных величин
Для дискретной случайной величины Х  функция распределения вероятностей имеет вид:
функция распределения вероятностей имеет вид: 
Тогда значение параметра  может быть равно …
может быть равно …
 | 0,655 |
Тема: Определение вероятности
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков не меньше девяти, равна …
 | 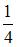 | ||
 | |||
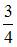 | |||
Решение:
Для вычисления события 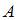 (сумма выпавших очков будет не меньше девяти) воспользуемся формулой
(сумма выпавших очков будет не меньше девяти) воспользуемся формулой  , где
, где 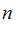 – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае возможны
– общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае возможны 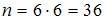 элементарных исходов испытания, из которых благоприятствующими являются исходы вида
элементарных исходов испытания, из которых благоприятствующими являются исходы вида  ,
, 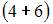 ,
,  ,
, 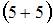 ,
,  ,
,  ,
,  ,
,  и
и  , то есть
, то есть 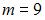 . Следовательно,
. Следовательно, 
Тема: Законы распределения вероятностей дискретных случайных величин
Для дискретной случайной величины 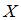 :
:

функция распределения вероятностей имеет вид:
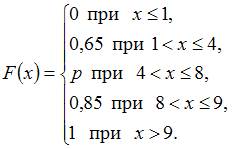
Тогда значение параметра 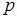 может быть равно …
может быть равно …
 | 0,7 | ||
| 0,85 | |||
| 0,6 |
Решение:
По определению  . Следовательно,
. Следовательно,  и
и 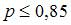 . Этим условиям удовлетворяет, например, значение
. Этим условиям удовлетворяет, например, значение 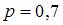
Тема: Числовые характеристики случайных величин
Непрерывная случайная величина 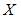 задана функцией распределения вероятностей:
задана функцией распределения вероятностей:

Тогда ее дисперсия равна …
 |  | ||
 | |||
 | |||
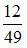 |
Решение:
Эта случайная величина распределена равномерно в интервале 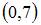 . Тогда ее дисперсию можно вычислить по формуле
. Тогда ее дисперсию можно вычислить по формуле 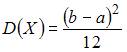 . То есть
. То есть 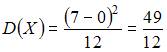
Тема: Полная вероятность. Формулы Байеса
В первой урне 6 черных шаров и 4 белых шара. Во второй урне 2 белых и 8 черных шаров. Из наудачу взятой урны вынули один шар, который оказался белым. Тогда вероятность того, что этот шар вынули из первой урны, равна …
 |  | ||
 | |||
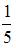 | |||
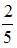 |
Решение:
Предварительно вычислим вероятность события A (вынутый наудачу шар – белый) по формуле полной вероятности:  . Здесь
. Здесь 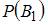 – вероятность того, что шар извлечен из первой урны;
– вероятность того, что шар извлечен из первой урны;  – вероятность того, что шар извлечен из второй урны;
– вероятность того, что шар извлечен из второй урны;  – условная вероятность того, что вынутый шар белый, если он извлечен из первой урны;
– условная вероятность того, что вынутый шар белый, если он извлечен из первой урны;  – условная вероятность того, что вынутый шар белый, если он извлечен из второй урны.
– условная вероятность того, что вынутый шар белый, если он извлечен из второй урны.
Тогда  .
.
Теперь вычислим условную вероятность того, что этот шар был извлечен из первой урны, по формуле Байеса: 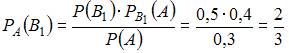
Тема: Числовые характеристики случайных величин
Дискретная случайная величина X задана законом распределения вероятностей:

Тогда ее дисперсия равна …
 | 7,56 | ||
| 3,2 | |||
| 3,36 | |||
| 6,0 |
Решение:
Дисперсию дискретной случайной величины 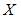 можно вычислить по формуле
можно вычислить по формуле
 . Тогда
. Тогда 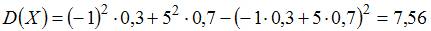
Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина 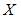 задана законом распределения вероятностей:
задана законом распределения вероятностей:

Тогда ее функция распределения вероятностей имеет вид …
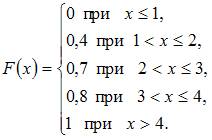
Решение:
По определению  . Тогда
. Тогда
а) при 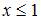 ,
, 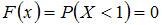 ,
,
б) при 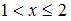 ,
,  ,
,
в) при 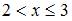 ,
, 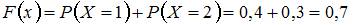 ,
,
г) при 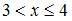 ,
,  ,
,
д) при  ,
,  .
.
Следовательно, 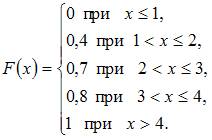
Тема: Определение вероятности
Внутрь круга радиуса 4 наудачу брошена точка. Тогда вероятность того, что точка окажется вне вписанного в круг квадрата, равна …
 |  |
Тема: Определение вероятности
В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет бракованных, равна …
 |  | ||
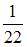 | |||
 | |||
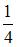 |
Решение:
Для вычисления события 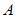 (среди отобранных деталей нет бракованных) воспользуемся формулой
(среди отобранных деталей нет бракованных) воспользуемся формулой  , где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события
, где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события 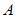 . В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно извлечь три детали из 12 имеющих, то есть
. В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно извлечь три детали из 12 имеющих, то есть 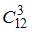 . А общее число благоприятствующих исходов равно числу способов, которыми можно извлечь три небракованные детали из семи, то есть
. А общее число благоприятствующих исходов равно числу способов, которыми можно извлечь три небракованные детали из семи, то есть 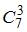 . Следовательно,
. Следовательно, 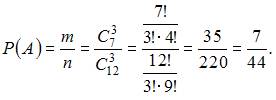
Тема: Полная вероятность. Формулы Байеса
Имеются три урны, содержащие по 5 белых и 5 черных шаров, и семь урн, содержащих по 6 белых и 4 черных шара. Из наудачу взятой урны вытаскивается один шар. Тогда вероятность того, что этот шар белый, равна …
 | 0,57 | ||
| 0,43 | |||
| 0,55 | |||
| 0,53 |
Решение:
Для вычисления вероятности события A (вынутый наудачу шар – белый) применим формулу полной вероятности:  . Здесь
. Здесь 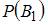 – вероятность того, что шар извлечен из первой серии урн;
– вероятность того, что шар извлечен из первой серии урн;  – вероятность того, что шар извлечен из второй серии урн;
– вероятность того, что шар извлечен из второй серии урн;  – условная вероятность того, что вынутый шар белый, если из он извлечен из первой серии урн;
– условная вероятность того, что вынутый шар белый, если из он извлечен из первой серии урн;  – условная вероятность того, что вынутый шар белый, если из он извлечен из второй серии урн.
– условная вероятность того, что вынутый шар белый, если из он извлечен из второй серии урн.
Тогда 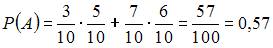
Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина 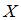 задана законом распределения вероятностей:
задана законом распределения вероятностей:

Тогда вероятность  равна …
равна …
 | 0,5 | ||
| 0,8 | |||
| 0,7 | |||
| 0,1 |
 ЗАДАНИЕ N 40 сообщить об ошибке
ЗАДАНИЕ N 40 сообщить об ошибке
Тема: Числовые характеристики случайных величин
Непрерывная случайная величина 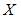 задана плотностью распределения вероятностей:
задана плотностью распределения вероятностей:
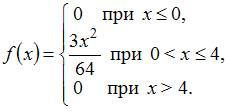
Тогда ее математическое ожидание равно …
 | |||
Решение:
Воспользуемся формулой  . Тогда
. Тогда 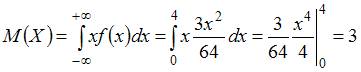
Тема: Полная вероятность. Формулы Байеса
Банк выдает 70% всех кредитов юридическим лицам, а 30% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,15; а для физического лица эта вероятность составляет 0,05. Получено сообщение о невозврате кредита. Тогда вероятность того, что этот кредит не погасило юридическое лицо, равна …
 | 0,875 | ||
| 0,125 | |||
| 0,105 | |||
| 0,375 |
Решение:
Предварительно вычислим вероятность события A (выданный кредит не будет погашен в срок) по формуле полной вероятности:  . Здесь
. Здесь 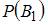 – вероятность того, что кредит был выдан юридическому лицу;
– вероятность того, что кредит был выдан юридическому лицу;  – вероятность того, что кредит был выдан физическому лицу;
– вероятность того, что кредит был выдан физическому лицу;  – условная вероятность того, что кредит не будет погашен в срок, если он был выдан юридическому лицу;
– условная вероятность того, что кредит не будет погашен в срок, если он был выдан юридическому лицу;  – условная вероятность того, что кредит не будет погашен в срок, если он был выдан физическому лицу. Тогда
– условная вероятность того, что кредит не будет погашен в срок, если он был выдан физическому лицу. Тогда
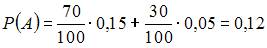 .
.
Теперь вычислим условную вероятность того, что этот кредит не погасило юридическое лицо, по формуле Байеса:
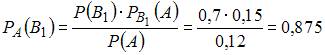 .
.
Тема: Числовые характеристики случайных величин
Непрерывная случайная величина 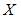 задана плотностью распределения вероятностей:
задана плотностью распределения вероятностей:
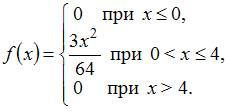
Тогда ее математическое ожидание равно …
 | |||
Решение:
Воспользуемся формулой  . Тогда
. Тогда 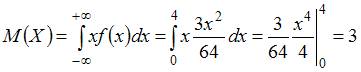 .
.
Тема: Определение вероятности
В круг радиуса 8 помещен меньший круг радиуса 5. Тогда вероятность того, что точка, наудачу брошенная в больший круг, попадет также и в меньший круг, равна …
 | 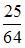 | ||
 | |||
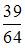 | |||
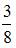 |
Решение:
Для вычисления вероятности искомого события воспользуемся формулой 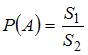 , где
, где 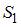 – площадь меньшего круга, а
– площадь меньшего круга, а 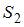 – площадь большего круга. Следовательно,
– площадь большего круга. Следовательно, 
Тема: Числовые характеристики случайных величин
Непрерывная случайная величина 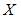 задана плотностью распределения вероятностей
задана плотностью распределения вероятностей  . Тогда математическое ожидание a и среднее квадратическое отклонение
. Тогда математическое ожидание a и среднее квадратическое отклонение  этой случайной величины равны …
этой случайной величины равны …
 | 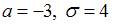 | ||
 | |||
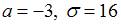 | |||
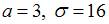 |
Решение:
Плотность распределения вероятностей нормально распределенной случайной величины 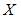 имеет вид
имеет вид 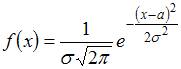 , где
, где  ,
,  . Поэтому
. Поэтому 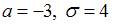 .
.
Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина 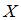 задана законом распределения вероятностей:
задана законом распределения вероятностей:

Тогда значения a и b могут быть равны …
 | 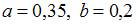 | ||
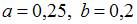 | |||
 | |||
 |
Решение:
Так как сумма вероятностей возможных значений 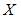 равна 1, то
равна 1, то  . Этому условию удовлетворяет ответ:
. Этому условию удовлетворяет ответ: 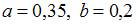 .
.
Тема: Определение вероятности
В круг радиуса 8 помещен меньший круг радиуса 5. Тогда вероятность того, что точка, наудачу брошенная в больший круг, попадет также и в меньший круг, равна …
 | 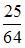 | ||
 | |||
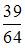 | |||
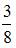 |
Решение:
Для вычисления вероятности искомого события воспользуемся формулой 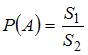 , где
, где 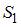 – площадь меньшего круга, а
– площадь меньшего круга, а 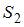 – площадь большего круга. Следовательно,
– площадь большего круга. Следовательно,  .
.
Тема: Полная вероятность. Формулы Байеса
В первой урне 3 черных шара и 7 белых шаров. Во второй урне 4 белых шара и 5 черных шаров. Из первой урны переложили один шар во вторую урну. Тогда вероятность того, что шар, вынутый наудачу из второй урны, будет белым, равна …
 | 0,47 | ||
| 0,55 | |||
| 0,35 | |||
| 0,50 |
Решение:
Для вычисления вероятности события A (вынутый наудачу шар – белый) применим формулу полной вероятности:  . Здесь
. Здесь 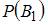 – вероятность того, что из первой урны переложили во вторую урну белый шар;
– вероятность того, что из первой урны переложили во вторую урну белый шар;  – вероятность того, что из первой урны переложили во вторую урну черный шар;
– вероятность того, что из первой урны переложили во вторую урну черный шар;  – условная вероятность того, что вынутый шар белый, если из первой урны во вторую был переложен белый шар;
– условная вероятность того, что вынутый шар белый, если из первой урны во вторую был переложен белый шар;  – условная вероятность того, что вынутый шар белый, если из первой урны во вторую был переложен черный шар.
– условная вероятность того, что вынутый шар белый, если из первой урны во вторую был переложен черный шар.
Тогда 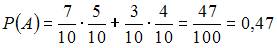
Тема: Законы распределения вероятностей дискретных случайных величин
Для дискретной случайной величины 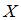 :
:

функция распределения вероятностей имеет вид:
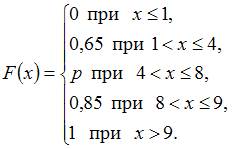
Тогда значение параметра 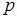 может быть равно …
может быть равно …
 | 0,7 | ||
| 0,85 | |||
| 0,6 |
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Полная вероятность. Формулы Байеса
Банк выдает 70% всех кредитов юридическим лицам, а 30% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,15; а для физического лица эта вероятность составляет 0,05. Получено сообщение о невозврате кредита. Тогда вероятность того, что этот кредит не погасило юридическое лицо, равна …
 | 0,875 | ||
| 0,125 | |||
| 0,105 | |||
| 0,375 |
Решение:
Предварительно вычислим вероятность события A (выданный кредит не будет погашен в срок) по формуле полной вероятности:  . Здесь
. Здесь 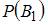 – вероятность того, что кредит был выдан юридическому лицу;
– вероятность того, что кредит был выдан юридическому лицу;  – вероятность того, что кредит был выдан физическому лицу;
– вероятность того, что кредит был выдан физическому лицу;  – условная вероятность того, что кредит не будет погашен в срок, если он был выдан юридическому лицу;
– условная вероятность того, что кредит не будет погашен в срок, если он был выдан юридическому лицу;  – условная вероятность того, что кредит не будет погашен в срок, если он был выдан физическому лицу. Тогда
– условная вероятность того, что кредит не будет погашен в срок, если он был выдан физическому лицу. Тогда
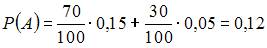 .
.
Теперь вычислим условную вероятность того, что этот кредит не погасило юридическое лицо, по формуле Байеса:
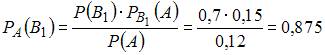 .
.
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Определение вероятности
В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет годных, равна …
 | 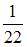 | ||
 | |||
 | |||
 |
Решение:
Для вычисления события 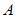 (среди отобранных деталей нет годных) воспользуемся формулой
(среди отобранных деталей нет годных) воспользуемся формулой  , где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события
, где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события 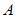 . В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно извлечь три детали из 12 имеющих, то есть
. В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно извлечь три детали из 12 имеющих, то есть 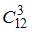 . А общее число благоприятствующих исходов равно числу способов, которыми можно извлечь три бракованные детали из пяти, то есть
. А общее число благоприятствующих исходов равно числу способов, которыми можно извлечь три бракованные детали из пяти, то есть 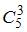 . Следовательно,
. Следовательно, 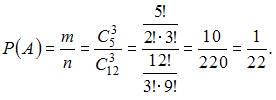
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Числовые характеристики случайных величин
Непрерывная случайная величина 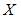 задана плотностью распределения вероятностей:
задана плотностью распределения вероятностей:

Тогда ее дисперсия равна …
 | 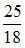 | ||
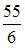 | |||
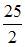 | |||
 |
Решение:
Дисперсию непрерывной случайной величины 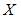 можно вычислить по формуле
можно вычислить по формуле
 Тогда
Тогда 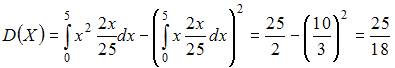
Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина 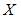 задана законом распределения вероятностей:
задана законом распределения вероятностей:

Тогда ее функция распределения вероятностей имеет вид …
 | 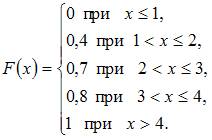 | ||
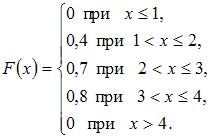 | |||
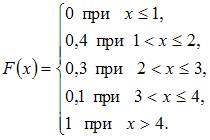 | |||
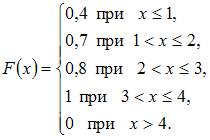 |
Решение:
По определению  . Тогда
. Тогда
а) при 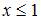 ,
, 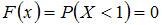 ,
,
б) при 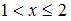 ,
,  ,
,
в) при 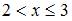 ,
, 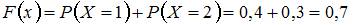 ,
,
г) при 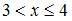 ,
,  ,
,
д) при  ,
,  .
.
Следовательно, 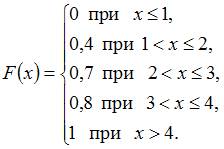
Тема: Полная вероятность. Формулы Байеса
Имеются три урны, содержащие по 5 белых и 5 черных шаров, и семь урн, содержащих по 6 белых и 4 черных шара. Из наудачу взятой урны вытаскивается один шар. Тогда вероятность того, что этот шар белый, равна …
 | 0,57 | ||
| 0,43 | |||
| 0,55 | |||
| 0,53 |
Решение:
Для вычисления вероятности события A (вынутый наудачу шар – белый) применим формулу полной вероятности:  . Здесь
. Здесь 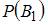 – вероятность того, что шар извлечен из первой серии урн;
– вероятность того, что шар извлечен из первой серии урн;  – вероятность того, что шар извлечен из второй серии урн;
– вероятность того, что шар извлечен из второй серии урн;  – условная вероятность того, что вынутый шар белый, если из он извлечен из первой серии урн;
– условная вероятность того, что вынутый шар белый, если из он извлечен из первой серии урн;  – условная вероятность того, что вынутый шар белый, если из он извлечен из второй серии урн.
– условная вероятность того, что вынутый шар белый, если из он извлечен из второй серии урн.
Тогда 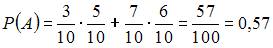 .
.
Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина 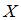 задана законом распределения вероятностей:
задана законом распределения вероятностей:

Тогда вероятность 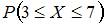 равна …
равна …
 | 0,8 | ||
| 0,3 | |||
| 0,7 | |||
| 0,4 |
Решение:
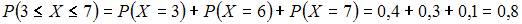 .
.
Тема: Числовые характеристики случайных величин
Дискретная случайная величина X задана законом распределения вероятностей:

Тогда ее дисперсия равна …
 | 7,56 | ||
| 3,2 | |||
| 3,36 | |||
| 6,0 |
Тема: Определение вероятности
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – десять, равна …
