Теорема Кронекера-Капелли.

Для совместности системы линейных уравнений необходимо и достаточно, чтобы ранг ее основной матрицы ( ) был равен рангу расширенной матрицы ( ).

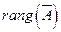Пусть = = 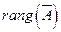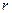. Тогда верны следующие утверждения.

Следствие 1.Если ранг матрицы 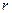равен числу неизвестных 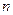, то система имеет единственное решение.

Следствие 2. Если ранг матрицы 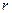меньше числа неизвестных, то система имеет бесконечное множество решений. При этом 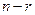неизвестных, которые называются свободными, принимают произвольные значения. Говорят, что система имеет 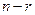степеней свободы.

Метод Гаусса (исключение неизвестных) состоит в том, что с помощью умножения уравнений на ненулевые числа и сложения в первом уравнении оставляем все неизвестные, во втором на одно меньше, в третьем на два меньше и т.д. Эту операцию (назовем ее процедурой Гаусса) удобно проводить, используя матрицы.

Составим расширенную матрицу системы и отделим для удобства свободные члены вертикальной линией. С помощью элементарных преобразований приводим матрицу к треугольному виду. Элементарные преобразования матрицы проводим только для строк.

Умножая первую строку на соответствующие коэффициенты и прибавляя к лежащим ниже строкам, получим нули в первом столбце. Затем проделываем такую же процедуру со второй строкой, третьей и т.д., до предпоследней строки. В результате преобразований получаем матрицу, по которой можно записать систему, равносильную исходной.

Рассмотрим три ситуации, возникающие при исследовании линейных систем.

1)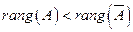 .Система несовместна.

►Пример 10.

Решить систему уравнений методом Гаусса:

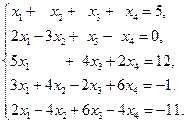
Решение.

Составим расширенную матрицу и преобразуем ее:

.

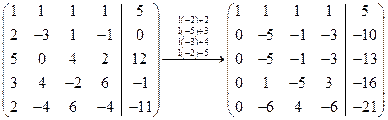Как и в примере 2 над стрелочкой указаны выполняемые операции.

Для удобства вычислений переставим четвертую строку на место второй и за счет второй строки получим нули во втором столбце во всех строках ниже второй, а затем за счет третьей строки - в третьем столбце:

В четвертой строке легко было получить нули, умножив третью строку на минус единицу и прибавив ее к четвертой. Мы не упрощали вычислений, чтобы сохранить алгоритм получения нулей в нижележащих строках за один шаг.

По преобразованной матрице определяем ранги: , , следовательно, данная система уравнений несовместна.

.

Ответ: система не имеет решений. ◄

2) .Система совместна и имеет единственное решение. В результате преобразований приходим к ступенчатой системе, решение которой легко находится.

►Пример 11.Решить систему уравнений методом Гаусса

Решение.

Составим расширенную матрицу и преобразуем ее:

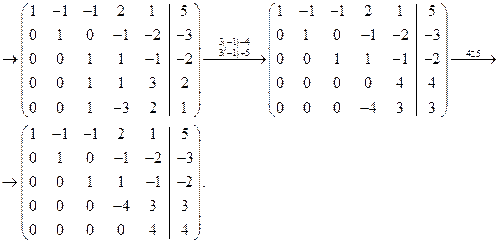
Ранг основной матрицы равен рангу расширенной матрицы и равен числу неизвестных. Следовательно, система совместна и имеет единственное решение. По преобразованной матрице составляем систему, равносильную исходной

Полученная система имеет ступенчатый вид и легко решается.

Ответ: .◄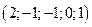

3)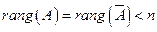 .Система совместна, но имеет бесконечное множество решений. Это множество решений находим, перенося члены со свободными неизвестными в правую часть уравнений.

►Пример 12.Решить систему уравнений

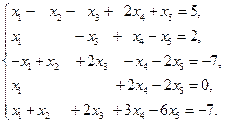
Решение.

Преобразуем расширенную матрицу системы

.

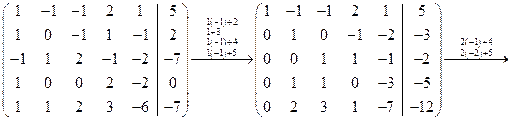
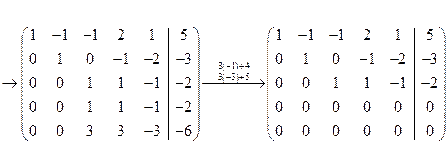Ранг основной матрицы равен рангу расширенной матрицы 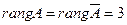, число неизвестных равно пяти. Следовательно, система совместна, но имеет бесконечное множество решений. Число степеней свободы равно двум. Выберем свободными неизвестными 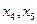и выразим через них:

отсюда получаем

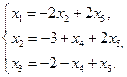
Ответ запишем в виде вектора-столбца.

Ответ: . ◄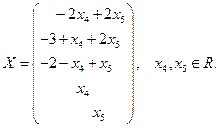

Упражнения.

Исследовать и решить системы уравнений:

1. Ответ: .

2. Ответ: .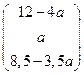

3. Ответ: .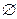

4. 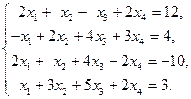Ответ: .

Индивидуальное задание

Каждый студент выполняет задание при конкретных значениях 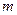и 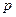, которые определяются по номеру в журнале группы: 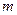−первая цифра номера по списку, 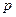− вторая. Если номер по списку однозначный .

№
№
№

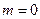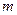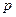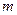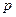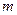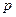1. Вычислить определители:

, , .

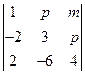2. Даны матрицы:

, , , .

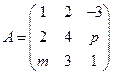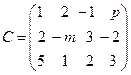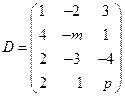Вычислить:

a) , где 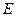- единичная матрица;

b) 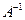(вычисления проводить, сохраняя три знака после запятой).

3.Решить системы уравнений двумя способами: по формулам Крамера и с помощью обратной матрицы:

а) б)

4. Исследовать и решить системы уравнений:

а)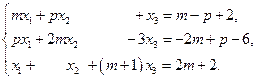

б)

в)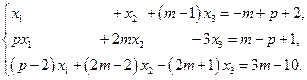

Приложение 1