Операции над множествами и их свойства

Основные понятия теории множеств

Понятие множества является фундаментальным понятием современной математики. Мы будем считать его первоначальным и теорию множеств строить интуитивно. Дадим описание этого первоначального понятия.

Множество – это совокупность объектов (предметов или понятий), которая мыслится как единое целое. Объекты, входящие в эту совокупность, называются элементами множества.

Можно говорить о множестве студентов первого курса математического факультета, о множестве рыб в океане и т.д. Математика обычно интересуется множеством математических объектов: множество рациональных чисел, множество прямоугольников и т.д.

Множества будем обозначать большими буквами латинского алфавита, а его элементы малыми.

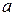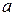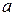Если – элемент множества M, то говорят « принадлежит M» и пишут: . Если некоторый объект не является элементом множества , то говорят « не принадлежит M» и пишут 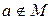(иногда ).

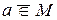Существует два основных способа задания множеств: перечисление его элементов и указание характеристического свойства его элементов. Первый из этих способов применяется, в основном, для конечных множеств. При перечислении элементов рассматриваемого множества его элементы обрамляются фигурными скобками. Например, обозначает множество, элементами которого являются числа 2, 4 , 7 и только они. Этот способ применим не всегда, так как, например, множество всех действительных чисел таким образом задать невозможно.

Характеристическое свойство элементов множества M – это такое свойство, что всякий элемент, обладающий этим свойством, принадлежит M, а всякий элемент, не обладающий этим свойством, не принадлежит M. Множество элементов, обладающих свойством , обозначается так:

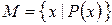или .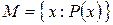

Наиболее часто встречающиеся множества имеют свои особые обозначения. В дальнейшем будем придерживаться следующих обозначений:

N =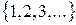 – множество всех натуральных чисел;

Z = 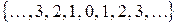– множество всех целых чисел;

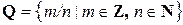– множество всех рациональных чисел;

R – множество всех действительных (вещественных) чисел, т.е. рациональных чисел (бесконечных десятичных периодических дробей) и иррациональных чисел (бесконечных десятичных непериодических дробей);

– множество всех комплексных чисел.

Приведем более специальные примеры задания множеств с помощью указания характеристического свойства.

Пример 1. Множество всех натуральных делителей числа 48 можно записать так: (запись используется только для целых чисел , 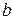и означает, что 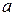делится на ).

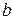Пример 2. Множество всех положительных рациональных чисел, меньших 7, записывается следующим образом: .

Пример 3. – интервал действительных чисел с концами 1 и 5; – отрезок действительных чисел с концами 2 и 7.

Слово «множество» наводит на мысль, что оно содержит много элементов. Но это не всегда так. В математике могут рассматриваться множества, содержащие только один элемент. Например, множество целых корней уравнения . Более того, удобно говорить о множестве, не содержащем ни одного элемента. Такое множество называется пустым и обозначается через Ø. Например, пустым является множество действительных корней уравнения .

Определение 1. Множества и называются равными (обозначается А=В), если эти множества состоят из одних и тех же элементов.

Определение 2. Если каждый элемент множества принадлежит множеству , то называют подмножеством множества .

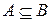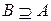Обозначения: (« включается в »); (« включает »).

Ясно, что Ø и само множество являются подмножествами множества . Всякое другое подмножество множества называется его правильной частью. Есл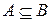и и , то говорят, что « А – собственное подмножество »или что «А строго включается в » и пишут .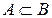

Очевидно следующее утверждение: множества и равны тогда и только тогда, когда 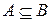и .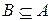

На этом утверждении основан универсальный метод доказательства равенства двух множеств: чтобы доказать, что множества и равны, достаточно показать, что является подмножеством множества , а является подмножеством множества .

Это наиболее употребительный способ, хотя и не единственный. Позже, познакомившись с операциями над множествами и их свойствами, мы укажем другой способ доказательства равенства двух множеств – с помощью преобразований.

В заключение заметим, что часто в той или иной математической теории имеют дело с подмножествами одного и того же множества U, которое называют универсальным в этой теории. Например, в школьной алгебре и математическом анализе универсальным является множество Rдействительных чисел, в геометрии – множество точек пространства.

Операции над множествами и их свойства

Над множествами можно выполнять действия (операции), напоминающие сложение, умножение и вычитание.

Определение 1. Объединением множеств и называется множество, обозначаемое через 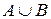, каждый элемент которого принадлежит хотя бы одному из множеств или .

Сама операция , в результате которой получается такое множество, называется объединением.

Краткая запись определения 1:

.

Определение 2. Пересечением множеств и называется множество, обозначаемое через , содержащее все те и только те элементы, каждый из которых принадлежит и , и .

Сама операция , в результате которой получается множество , называется пересечением.

Краткая запись определения 2:

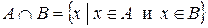
Например, если , , 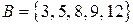то , .

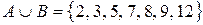Множества можно изображать в виде геометрических фигур, что позволяет наглядно иллюстрировать операции над множествами. Такой метод был предложен Леонардом Эйлером (1707–1783) для анализа логических рассуждений, широко применялся и получил дальнейшее развитие в трудах английского математика Джона Венна (1834–1923). Поэтому такие рисунки называют диаграммами Эйлера-Венна.

Операции объединения и пересечения множеств можно проиллюстрировать диаграммами Эйлера–Венна следующим образом:

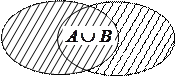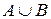– заштрихованная часть; – заштрихованная часть.

Рис. 1.

Можно определить объединение и пересечение любой совокупности множеств , где – некоторое множество индексов.

Определение . Объединением совокупности множеств называется множество , состоящее из всех тех и только тех элементов, каждый из которых принадлежит по крайней мере одному из множеств .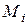

Определение 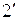. Пересечением совокупности множеств называется множество , состоящее из всех тех и только тех элементов, каждый из которых принадлежит любому из множеств .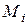

В случае, когда множество индексов конечно, например, , то для обозначения объединения и пересечения совокупности множеств в этом случае обычно пользуются обозначениями:

и .

Например, если , , 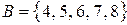, то , .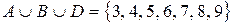

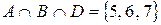С понятиями объединения и пересечения множеств неоднократно встречаются в школьном курсе математики.

Пример 1.Множество М решений системы неравенств

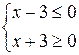
является пересечением множеств решений каждого из неравенств этой системы: .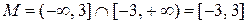

Пример 2.Множество М решений системы

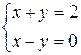
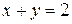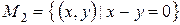является пересечением множеств решений каждого из неравенств этой системы. Множество решений первого уравнения – множество точек прямой , т.е. . Множество . Множество состоит из одного элемента – точки пересечения прямых.

Пример 3.Множество решений уравнения

,

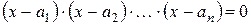где , является объединением множеств решений каждого из уравнений , , 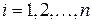т.е.

.

Определение 3. Разностью множеств и называется множество, обозначаемое через 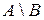, и состоящее из всех тех и только тех элементов, которые принадлежат , но не принадлежат .

Определение 4. Если U – универсальное множество и 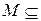U, то разность U 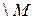называется дополнением множества М (до U) и обозначается через 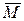, , 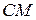, или .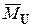

Краткие записи определений 3 и 4:

, = .

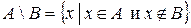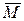Операции разности и дополнения множеств можно проиллюстрировать диаграммами Эйлера-Венна:

– заштрихованная часть;

– заштрихованная часть.

Рис. 2.

Пример 4.Если , , то , .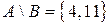

Определение 5. Объединение множеств 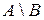и 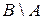называется симметрической разностью множеств , и обозначается через 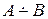, т.е.

.

Понятно, что .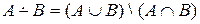

Следующий пример иллюстрирует симметрическую разность множеств и показывают, что операция разности множеств не обладает свойством коммутативности (переместительности), и демонстрируют некоторые возможные частные случаи для разности множеств A и B .

Пример 5.

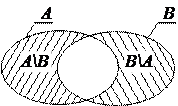а) б)

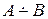– заштрихованная часть; ; 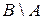– заштрихованная часть.

в)

; .

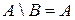Рис. 3.

Обозначим через B(U) множество всех подмножеств универсального множества U с операциями объединения, пересечения и дополнения. Полученную математическую структуру называют алгеброй множествилиалгеброй Булямножеств(вчесть ирландского математика и логика Джорджа Буля (1816–1864)). Через 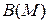будем обозначать множество всех подмножеств произвольного множества и называть его булеаном множества .

Перечисленные ниже равенства справедливы для любых подмножеств A, B, C универсального множества U.Поэтому их и называют законами алгебры множеств.