Правила вычисления пределов

При вычислении пределов следует учитывать следующие основные правила:

1. Предел суммы (разности) функций равен сумме (разности) пределов слагаемых:

.

2. Предел произведения функций равен произведению пределов сомножителей:

.

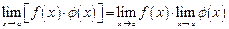3. Предел отношения двух функций равен отношению пределов этих функций:

.

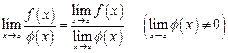4. Постоянный множитель можно выносить за знак предела:

.

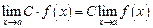5. Предел постоянной равен самой постоянной:

.

6. Для непрерывных функций символы предела и функции можно поменять местами:

.

Нахождение предела функции 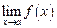следует начинать с подстановки значения 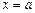в выражение для функции. При этом если получается числовое значение 0 или ¥, то искомый предел найден.

Пример 2.1.Вычислить предел .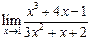

Решение.

.

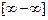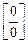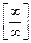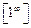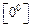
Выражения вида , , , , , 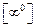называются неопределённостями.

Если получается неопределенность вида , то для нахождения предела нужно преобразовать функцию так, чтобы раскрыть эту неопределенность.

Неопределенность вида 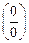обычно получается, когда задан предел отношения двух многочленов. В этом случае, для вычисления предела рекомендуется разложить многочлены на множители и сократить на общий множитель. Этот множитель равен нулю при предельном значении х.

Пример 2.2.Вычислить предел .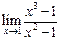

Решение.

Подставляя 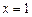, получим неопределенность:

.

Разложим числитель и знаменатель на множители:

;

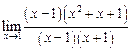Сократим на общий множитель 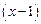и получим

.

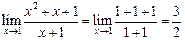Неопределенность вида 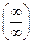получается, когда задан предел отношения двух многочленов при 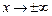. В этом случае для вычисления рекомендуется разделить оба многочлена на х в старшей степени.

Пример 2.3. Вычислить предел .

Решение.При подстановке ∞ получается неопределенность вида 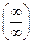, поэтому разделим все члены выражения на x³.

.

Здесь учитывается, что .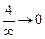

При вычислении пределов функции, содержащей корни, рекомендуется умножить и разделить функцию на сопряженное выражение.

Пример 2.4.Вычислить предел

Решение.

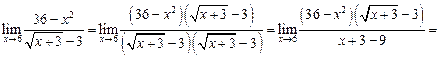
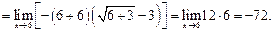
При вычислении пределов для раскрытия неопределенности вида 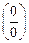или (1)^∞ часто используются первый и второй замечательные пределы:

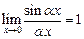
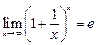и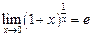

Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины.

Рассмотрим пример Я. И. Перельмана, дающий интерпретацию числа e в задаче о сложных процентах. В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример.

Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед.

Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 × 1,5 = 150, а еще через полгода - в 150 × 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 × (1 +1/3)³ »237 (ден. ед.).

Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:

100 × (1 +1/10)¹⁰ » 259 (ден. ед.),

100 × (1+1/100)¹⁰⁰ » 270 (ден. ед.),

100 × (1+1/1000)¹⁰⁰⁰ » 271 (ден. ед.).

При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что

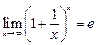
Пример 2.5.Вычислить предел функции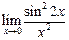

Решение.

Пример 2.6.Вычислить предел функции .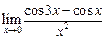

Решение.Подставляя 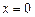получим неопределенность:

.

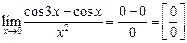Используя тригонометрическую формулу, преобразуем числитель в произведение:

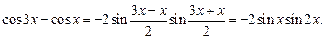
В результате получаем

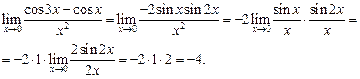
Здесь учитывается второй замечательный предел .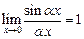

Пример 2.7.Вычислить предел функции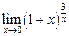

Решение.

.

Для раскрытия неопределенности вида 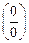или 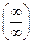можно использовать правило Лопиталя, которое основано на следующей теореме.

Теорема.Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных

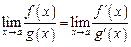
Заметим, что это правило можно применять несколько раз подряд.

Пример 2.8. Найти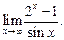

Решение.При подстановке 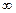, имеем неопределенность вида 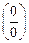. Применяя правило Лопиталя, получим

Непрерывность функции

Важным свойством функции является непрерывность.

Определение.Функция считается непрерывной, если малое изменение значения аргумента влечет за собой малое изменение значения функции.

Математически это записывается так: при

Под 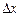и 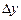понимается приращение переменных, то есть разность между последующим и предыдущим значениями: 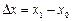, 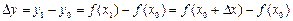(рисунок 2.3)

Рисунок 2.3 – Приращение переменных

Из определения функции 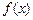, непрерывной в точке , следует, что . Это равенство означает выполнение трех условий:

1) функция 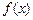определена в точке и ее окрестности функция ;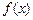

2) функция 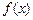имеет предел при 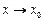или, что равносильно, существуют и равны односторонние пределы 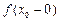и ;

3) предел функци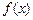и при 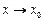равен значению функции в точке .

Если нарушается хотя бы одно из этих условий, то точку называют точкой разрыва функции. Выделяют следующие типы точек разрыва.

1) Если в точке разрыва существуют односторонние конечные пределы функции, то называют точкой разрыва первого рода.

При этом если односторонние пределы совпадают, то называют точкой устранимого разрыва первого рода, если односторонние пределы не совпадают, то называют точкой конечного разрыва первого рода (или точкой скачка)

2) Если в точке хотя бы один из односторонних пределов функции не существует или бесконечен, то называют точкой разрыва второго рода.

Пример 2.9.Найти точки разрыва функции:

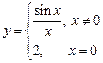
Решение.Для функции 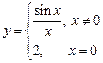точка 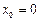является подозрительной на разрыв, проверим это, найдем односторонние пределы

Следовательно, 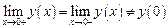, значит 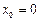- точка устранимого разрыва

Производная функции