Формула и ряд Тейлора. Биноминальный ряд
Рассмотрим многочлен 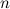 -й степени
-й степени
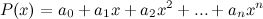
Его можно представить в виде суммы степеней  , взятых с некоторыми коэффициентами. Продифференцируем его
, взятых с некоторыми коэффициентами. Продифференцируем его 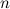 раз по переменной
раз по переменной  , а затем найдем значения многочлена и его производных в точке
, а затем найдем значения многочлена и его производных в точке 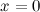 :
:
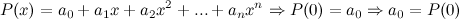

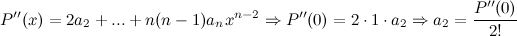

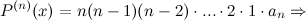
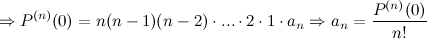
Таким образом, получаем, что

Полученное выражение называется формулой Маклорена для многочлена 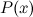 степени
степени 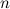 .
.
Рассуждая аналогично, можно разложить многочлен 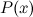 по степеням разности
по степеням разности 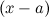 , где
, где  - любое число. В этом случае будем иметь:
- любое число. В этом случае будем иметь:
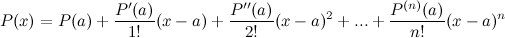
Это выражение называется формулой Тейлора для многочлена 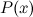 в окрестности точки
в окрестности точки  .
.
Пример
Задание. Разложить в ряд Тейлора функцию  в точке
в точке  .
.
Решение. Найдем производные:
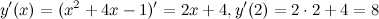


Итак,  ,
, 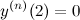 ,
, 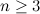 . Значение функции в точке
. Значение функции в точке
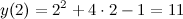
Таким образом,
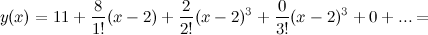
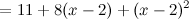
Ответ. 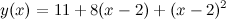
БИНОМИАЛЬНЫЙ РЯД - степенной ряд вида

где n - целое, а α - произвольное фиксированное число (вообще говоря, комплексное), z = x + iy - комплексное переменное, (αn) - биномиальные коэффициенты. Для целых α = m ≥ 0 Б. р. сводится к конечной сумме m + 1 слагаемых

называемой Ньютона биномом. Для остальных значений α Б. р. абсолютно сходится при |z| < 1 и расходится при |z| > 1. В граничных точках единичной окружности |z| = 1 Б. р. ведет себя следующим образом: 1) если Re α > 0, то он абсолютно сходится во всех точках окружности |z| = 1; 2) если Re α ≤ - 1, то он расходится во всех точках окружности |z| = 1; 3) если - 1 < Rе α ≤ 0, то Б. р. расходится в точке z = - 1 и условно сходится во всех остальных точках окружности |z| = 1. Во всех точках, в к-рых Б. р. сходится, он представляет главное значение функции (1 + z)α, равное 1 при z = 0. Б. р. является частным случаем гипергеометрического ряда.
Если z = x и α - действительные числа, причем α не есть целое неотрицательное число, то Б. р. ведет себя следующим образом: 1) если α > 0, то он абсолютно сходится при - 1 ≤ x ≤ 1 2) если α ≤ - 1, то Б. р. абсолютно сходится при - 1 < x < 1 и расходится при всех иных значениях х; 3) если - 1 < α ≤ 0, то Б. р. абсолютно сходится при - 1 < x < 1, условно сходится при х = 1 и расходится при х = - 1; при |х| > 1 Б. р. всегда расходится.
Теорема Эйлера. Правильные многогранники.
Выпуклый многогранник называется правильным, если его гранями являются равные правильные многоугольники, и в каждой вершине сходится одинаковое число граней.
Пусть дан топологически правильный многогранник, гранями которого являются n - угольники, и в каждой вершине сходится m ребер. Ясно, что n и m больше или равны трем. Обозначим, как и раньше, В - число вершин, Р - число ребер и Г - число граней этого многогранника. Тогда
nГ = 2P; Г = 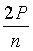 ; mB = 2P; В =
; mB = 2P; В =  .
.
По теореме Эйлера, В - Р + Г = 2 и, следовательно,
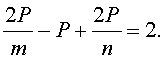
Откуда Р =  .
.
Из полученного равенства, в частности, следует, что должно выполняться неравенство 2n + 2m – nm > 0, которое эквивалентно неравенству (n – 2)(m – 2) < 4.
Теорема Эйлера
Для любого выпуклого многогранника справедливо соотношение Г+В-Р=2, где Г – число граней, В – число вершин и Р – число ребер данного многогранника.
Доказательство теоремы, связанное с нахождением суммы плоских углов выпуклого многогранника:
Обозначим эту сумму, как  . Напомним, что плоскими углами многогранника являются внутренние плоские углы его граней.
. Напомним, что плоскими углами многогранника являются внутренние плоские углы его граней.
Например, найдем  для таких многогранников:
для таких многогранников:
а) тетраэдр имеет 4 грани – все треугольники. Таким образом,  ;
;
б) куб имеет 6 граней – все квадраты. Таким образом, 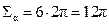 ;
;
в) возьмем теперь произвольную пятиугольную призму. У нее две грани – пятиугольники и пять граней – параллелограммы. Сумма углов выпуклого пятиугольника равна 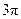 . Сумма углов параллелограмма равна
. Сумма углов параллелограмма равна 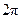 . Таким образом,
. Таким образом, 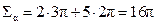 .
.
Итак, для нахождения  мы вычисляли сначала сумму углов, принадлежащих каждой грани. Воспользуемся этим приемом и в общем случае.
мы вычисляли сначала сумму углов, принадлежащих каждой грани. Воспользуемся этим приемом и в общем случае.
Введем следующие обозначения: 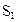 ,
,  ,
, 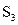 …,
…,  - число сторон в 1, 2, 3-й и т.д. последней грани многогранника.
- число сторон в 1, 2, 3-й и т.д. последней грани многогранника.
Тогда 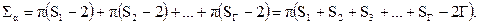
Далее найдем общее число сторон всех граней многогранника. Оно равно 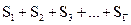 . Так как каждое ребро многогранника принадлежит двум граням, имеем:
. Так как каждое ребро многогранника принадлежит двум граням, имеем: 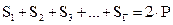 .
.
Таким образом, получаем:
 (1)
(1)
Сосчитаем теперь  другим способом. Для этого будем менять форму многогранника таким образом, что бы у него не менялось число Г, В и Р. При этом может измениться каждый плоский угол в отдельности, но число
другим способом. Для этого будем менять форму многогранника таким образом, что бы у него не менялось число Г, В и Р. При этом может измениться каждый плоский угол в отдельности, но число  останется прежним. Выберем такое преобразование многогранника: примем одну из его граней за основание, расположим его горизонтально и «растянем» для того, чтобы на него можно было спроектировать другие грани многогранника. Например, на рисунке 1а показано, к чему мы придем, в случае тетраэдра, а на рисунке 1б – в случае куба
останется прежним. Выберем такое преобразование многогранника: примем одну из его граней за основание, расположим его горизонтально и «растянем» для того, чтобы на него можно было спроектировать другие грани многогранника. Например, на рисунке 1а показано, к чему мы придем, в случае тетраэдра, а на рисунке 1б – в случае куба
Заметим, что спроектированный многогранник представляет слившиеся две наложенные друг на друга пластины с общим контуром, из которых верхняя разбита на (Г-1) многоугольник, а нижняя на грани не делится. Обозначим число сторон внешнего окаймляющего многоугольника через r. Теперь найдем  спроектированного многоугольника.
спроектированного многоугольника.  состоит из следующих трех сумм:
состоит из следующих трех сумм:
1) Сумма углов нижней грани, у которой r сторон, равна 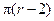 .
.
2) Сумма углов верхней пластины, вершинами которых являются вершины нижней грани, тоже равна 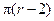 .
.
3) Сумма «внутренних» углов верхней пластины равна 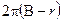 , так как верхняя пластина имеет
, так как верхняя пластина имеет  внутренних вершин и все углы группируются около них.
внутренних вершин и все углы группируются около них.
Итак,  (2)
(2)
Таким образом, сравнивая выражения (1) и (2), получаем: Г+В-Р=2, что и требовалось доказать.
