Тотожна рівність двох многочленів

Розглянемо два многочлени n-го степеня:

,

.

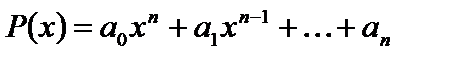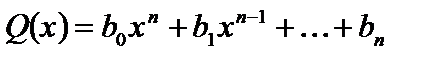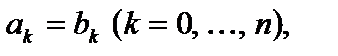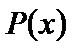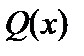Означення. Якщо тобто всі відповідні коефіцієнти многочленів рівні між собою, то говорять, що многочлени і тотожно рівні між собою. Записують: .

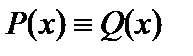Теорема. Якщо 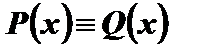, то відповідні коефіцієнти много-
членів однакові:

.

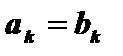
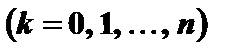Теорема. Якщо значення двох многочленів n-го степеня збігаються в 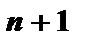точці, то многочлени тотожно рівні між собою.

3. Розкладання на множники.

Якщо многочлен з дійсними коефіцієнтами має комплексний корінь 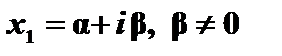, то він має і комплексно спряжений корінь .

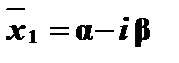Візьмемо довільний многочлен з дійсними коефіцієнтами й розкладемо його на лінійні множники:

.

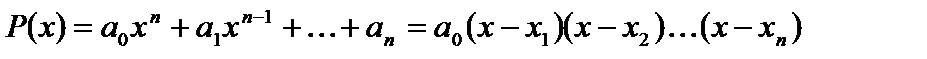Серед коренів можуть бути дійсні та комплексні. Згрупувавши однакові корені, дістанемо:

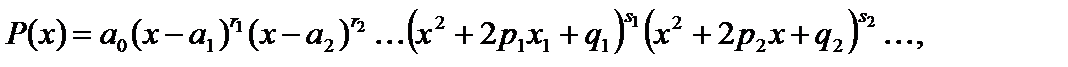
де 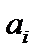— дійсні корені многочлена 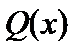; 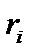— цілі числа, так зва-
ні кратності коренів многочлена; 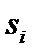— цілі числа, так звані крат-
ності квадратних тричленів; 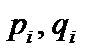— дійсні числа. При цьому 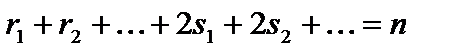, де n — степінь многочлена .

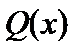Список використаних джерел

1) Дубовик В. П. Вища математика: навчальний посібник / В. П. Дубовик, І. І. Юрик; за ред. В.П. Дубовика, І.І. Юрика. – К. : А.С.К., 2005. – 648 с. : іл. , ст. 347-349

Контрольні питання

1. Які рівняння називаються алгебраїчними рівняннями п-го порядку.

2. Сформулювати теорему Безу.

3. Сформулювати теорему про розклад многочлена на лінійні множники.

4. Розкласти на множники многочлен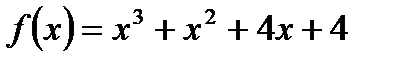

Самостійна робота № 18

Тема. Інтеграли, які не виражаються через елементарні функції.

Мета: знати інтеграли, які не виражаються через елементарні функції.

Кількість годин: 2

План

1. Інтеграли, що «не беруться».

2. Види інтегралів, що «не беруться».

1. Інтеграли, що «не беруться».

Інтегрування елементарних функцій не завжди знову приводить до елементарних функцій. Інтеграли хоча йіснують, але не є елементарними функціями. В подібних випадках первісна являє собою деяку, нову, неелементарну функцію,тобто функціЮ,яка не виражається через скінченне число арифметичних операцій ісуперпозицій над основними елементарними функціями.

2. Види інтегралів, що «не беруться».

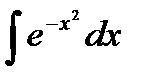- інтеграл Пуассона;

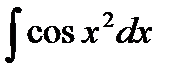
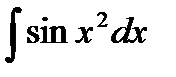- інтеграли Френеля;

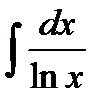- інтегральний логарифм;

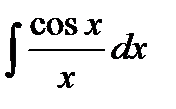- інтегральний косинус;

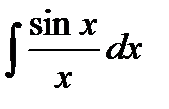- інтегральний синус;

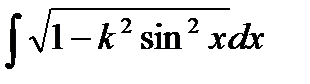- еліптичний інтеграл.

Список використаних джерел

1) Дубовик В. П. Вища математика: навчальний посібник / В. П. Дубовик, І. І. Юрик; за ред. В.П. Дубовика, І.І. Юрика. – К. : А.С.К., 2005. – 648 с. : іл., ст. 361-362

Контрольні питання

1. У якому випадку кажуть, що невизначений інтеграл не є елементарною функцією?

2. Навести приклади інтегралів, що «не беруться».

Самостійна робота № 19

Тема. Застосування визначених інтегралів до обчислення фізичних величин.

Мета: знати застосування визначених інтегралів до обчислення фізичних величин.

Кількість годин: 2

План

1. Обчислення роботи

2. Обчислення тиску рідини на вертикальну пластину

1. Обчислення роботи

Нехай під дією сили 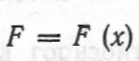матеріальна точка рухається вздовж прямої лінії. Якщо напрям руху збігається з напрямом сили, то, як відомо (п. 2.1), робота А, виконана з цією силою при переміщенні точки на відрізок [а; b], обчислюється за формулою

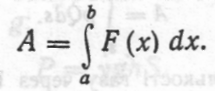(82)

Приклади

1. Обчислити роботу, яку треба затратити, щоб тіло маси m підняти з поверхні Землі вертикально вверх на висоту h, якщо радіус Землі дорівнює R.

О Згідно з законом Ньютона, сила F притягання тіла Землею дорівнює

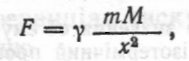
де M — маса Землі; 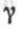— гравітаційна стала; x — відстань від центра тіла до центра землі. Покладемо сталу 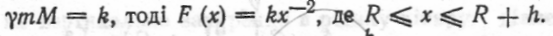При х 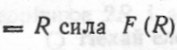дорівнює вазі тіла 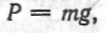тобто 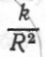= P, звідки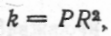 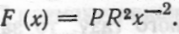За формулою (82) маємо

•

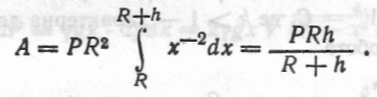2. Яка робота виконується під час стискання гвинтової пружини на 5 см, якщо-для стискання пружини на 1 см витрачається сила 4 H. Стиск гвинтової пружини пропорційний прикладеній силі.

О Сила F і стискання х за умовою пропорційні: 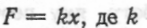— стала. При х 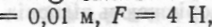тому з рівності 4 =k*0,01 знаходимо k=400, отже F(x) 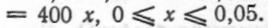Тому за формулою (82) маємо

•

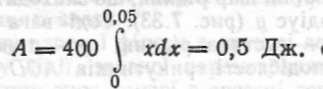3. Нехай у циліндрі з рухомим поршнем (рис. 7.32) знаходиться деяка кількість газу. Припустимо, що цей газ розширився і пересунув поршень вправо. Яку роботу виконує при цьому газ?

О Нехай 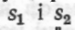— початкова і кінцева відстані поршня від лівого дна циліндра;

s — шлях, на який перемістився поршень; ρ — тиск газу на одиницю площі порш­ня; Q — площа поршня. Оскільки вся сила, що діє на поршень, дорівнює ρQ, то

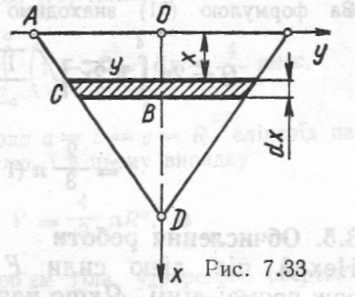
виконана при виштовхуванні поршня робота А виразиться інтегралом

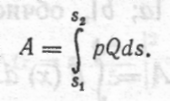
Позначаючи об'єм даної кількості газу через 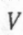, дістанемо, що 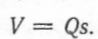Переходячи в інтегралі від змінної s до нової змінної 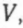виразимо роботу через об'єм:

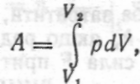
де 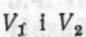— початкове і кінцеве значення об'єму V.

Зокрема, якщо йдеться про ізотермічний процес розширення газу, то, згідні з законом Бойля — Маріотта, 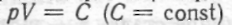і тоді робота

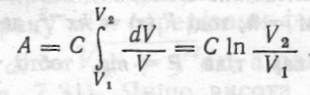
Якщо розглядається адіабатичний процес розширення ідеального газу, то зі законом Пуассона маємо 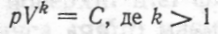— характерна для кожного газу стала. Звідси 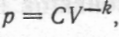тому робота

•

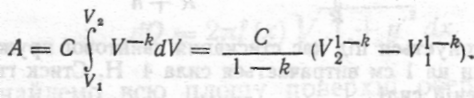4. Знайти роботу, яку необхідно затратити, щоб викачати рідину з конічного резервуара, оберненого вершиною вниз. Радіус і висота конуса дорівнюють відповідно R і H.

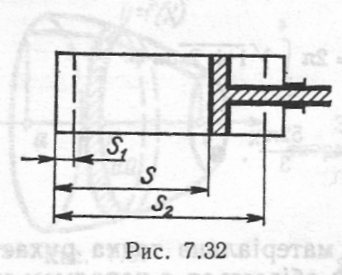
О Вважатимемо елементарний шар рідини, що знаходиться на глибині x, циліндром, який має висоту dx і радіус у (рис. 7.33). Тоді вага 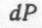цього шару дорівнює 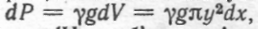де у — густина рідини, g — прискорення вільного падіння, dV —об'єм циліндра. 3 подібності трикутників AOD і CBD знаходимо у:

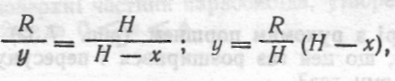
тому

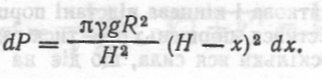
Елементарна робота, яку необхідно затратити, щоб підняти цей шар рідини на висоту x, дорівнює

•

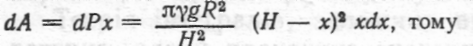
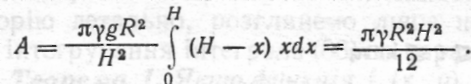2. Обчислення тиску рідини на вертикальну пластину

Як відомо, тиск рідини на горизонтальну площадку, занурену в рідину, визначається за законом Паскаля: тиск P рідини на площадку дорівнює її площі S, помноженій на глибину занурення h густину рідини у і на прискорення вільного падіння g:

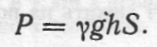
Якщо в рідину занурити не горизонтальну площадку, то її різні точки лежатимуть на різних глибинах і цією формулою користуватись не можна. Проте якщо площадка дуже мала, то всі її точки лежать на майже одній глибині, яку вважають за глибину занурення площадки. Це дає змогу знайти диференціал тиску на елементарну площадку, а потім тиск на всю поверхню.

Приклад

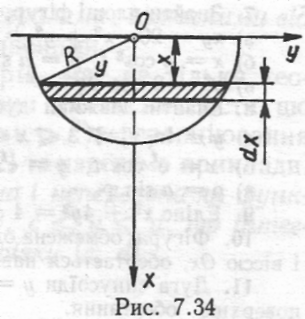
Знайти тиск рідини на вертикально занурений в рідину півкруг, діаметр якого дорівнює 2R і знаходиться на поверхні рідини.

Нехай елементарна площадка знаходиться на глибині x (рис. 7.34). Вважаючи її прямокутником з основою 2y і висотою dx, знайдемо за законом Паскаля диференціал тиску:

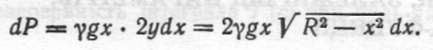
Звідси

•

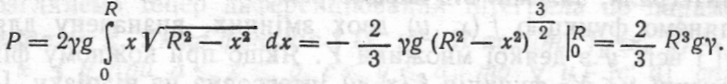Список використаних джерел

1) Дубовик В. П. Вища математика: навчальний посібник / В. П. Дубовик, І. І. Юрик; за ред. В.П. Дубовика, І.І. Юрика. – К. : А.С.К., 2005. – 648 с. : іл. , ст. 385-388

Контрольні питання

1. Як знаходити роботу?

2. Як обчислити тиск рідини на вертикальну пластину?

Самостійна робота № 20

Тема. Застосування диференціальних рівнянь.

Мета: знати задачі, які приводять до ДР 1-го порядку.

Кількість годин: 2

План

1. Задача про радіоактивний розпад.

2. Задача про силу струму.

1. Задача про радіоактивний розпад.

Встановлено, що швидкість радіоактивного розпаду речовини пропорційна її кількості вданий момент часу. Знайти закон зміни маси речовини від часу, якщо при t = 0 маса речовини дорівнювала m₀.

Нехай 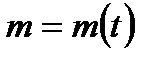- маса речовини в момент часу t. За умовою 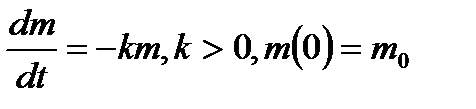, де к – коефіцієнт пропорційності. Знак мінус береться тому, що з часом маса речовини зменшується.

Розвязуючи знайдене рівняння, дістаємо, що .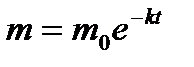

2. Задача про силу струму.

Треба знайти залежність сили струму і від часу t в контурі, який має електрорушійну силу ε, опір R та індуктивність L.

Згідно з законом Ома, маємо: 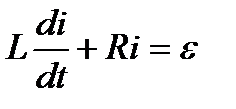. Розвязуючи це лінійне рівняння, дістаємо загальний розвязок 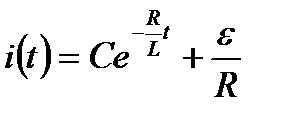, де С – довільна стала. При t = 0 маємо і(0) = 0, тому С= - ε/R. Отже, дістаємо:

.

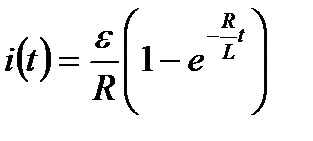Звідки видно, що сила струму при 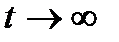наближається до свого стаціонарного значення .

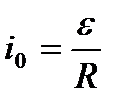Контрольні питання

1. У чому полягає задача про радіоактивний розпад.

2. У чому полягає задача про силу струму.

Список використаних джерел

1) Дубовик В. П. Вища математика: навчальний посібник / В. П. Дубовик, І. І. Юрик; за ред. В.П. Дубовика, І.І. Юрика. – К. : А.С.К., 2005. – 648 с. : іл. , ст. 446-450

Самостійна робота № 21

Тема. Системи диференціальних рівнянь.

Мета: знати поняття систем диференціальних рівнянь та вміти їх розв'язувати.

Кількість годин: 2

План

1. Системи диференціальних рівнянь.

2. Метод підстановки розв’язування систем ДР.