Непрерывные случайные величины

Опр. Пусть существует неотрицательная функция p(x),удовлетворяющая при любых х равенству

F(x)=P{X<x}_-∞∫^x p(t) dt

Случайные величины, обладающие этим свойством, называются непрерывными. Функция p(x) называется плотностью распределения вероятностей случайной величины X, а F(x) — её

функция распределения

Опр. Мат. ожид. случ. непрер. величины X называется интеграл _-∞∫^∞ xp(x) dx, где p(x) – плотность распределения вероятности сл. велич. X.

Опр. Дисперсией непр. сл. велич. X называется интеграл _-∞∫^∞ (x-MX)² p(x) dx, где p(x) – плотность распределения вероятности сл. велич. X.

Опр. Плотностью совместного распределения 2-х случайных величин X и Y, заданных на одном и том же пр-ве элементарных соб., называется такая неотрицательная функция 2-х переменных p(u,v), что для любых x и y справедливо равенство:

P{X<x,Y<y}_-∞∫^x_-∞∫^y p(u,v) du dv.

Опр. Ковариацией 2-х непрерывных случайных величин X и Y называется мат. ожидание случайной величины (X-MX) (Y-MY), которое выражается в виде интеграла:

Соv (X,Y)=_-∞∫^∞ _-∞∫^∞ (x-MX)(y-MY)p(x,y) dxdy

Опр. Коэффиц. корреляции 2-х непрерывн. сл. велич. X и Y называется число

ρ(X,Y)=(Cov(X,Y))/√DX DY

№10. Свойства мат. ожидания и дисперсии сл. вел-ны, плотность вероятности и ее св-ва.

МХ: 1^о. М(Х+Y)=МХ+MY(аддитивность). Док: = , = 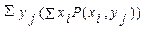. Построим Σ мат-их ожиданий MX+MY= 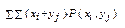=М(Х+Y)_■ 2^о. М(Х₁+Х₂+…+Х_n)=МХ₁+ МХ₂+…+ МХ_n.(док. из 1^о). 3^о. Если с = const, то Мс=с. 4^о. Если случ-ые вел-ны Х и Y независимы, то М(ХY)=MX+MY. Док: Т.к. Х и Y незав-мы, то P(x_i, y_j)= P(x_i) P(y_j). Тогда М(ХY)= 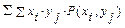= =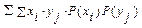MХ·MY_■ 5^о. |М(ХY)| (нерав-во Коши-Буняковского). Док: " а справ-во нер-во 0 £ М (аХ+Y)²=a²·MX²+ 2a·MX·MY+MY² – квадратичн. трехчлен). Дискрим. долж. быть £ 0. 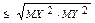D/4=(M(XY))² - MX²·MY² £ 0 Þ |М(ХY)| _■ Св-ва MX и DX непрер-ых сл. вел-н и дискретн. сл. вел. соответ-но совпадают.

DX: 1^о. DX ³ 0. Док: P(X) ³ 0, MX² ³ 0 ÞDX ³ 0. 2^о. Dс = 0, с = const. Док: Мс = с, Р(с) =1Þ Dс=M(C –Mс)² =M(0)=0·1=0_■ 3^о. Пост-ый множитель можно выносить за знак дисперс., при этом возводя его в квадр. D(сX) =с²DX. Док: По опред D(сX) =M(сX–M(сX))²= M(сX–с·MX)²=M [с²·(X–MX)²]=с²·M(X–MX)² =с²·DX_■ 4^о. DX =M(X²)–(MX)². Дисп. случ. вел-ны Х= разности мат. ожид-ия квадрата сл. вел-ны Х и квадрата мат. ожид-ия сл. вел-ны Х. Док: DX =M(X–MX)²= M(X²–2X·MX+(MX)²)=M(X²)–2M(X–MX)+(MX)²=M(X²)–2MX–MX+(MX)²=M(X)²–(MX)²_■

Опр. Пусть $ неотриц-ая ф-ия р(Х) удовлетв-щая при люб. х рав-ву F(X)=P{X<x}= 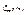Сл. вел-ны, облад-щие этими св-ми наз-ся непреравн. Ф-ия р(Х) – плотность распр-ия вероят-ей сл. вел-ны Х, ф-ия F(X) – ф-ия распр. Случай, когд. F(X) диффер-ма: Св-ва плотн-ти: 1^о. р(Х) ³ 0. 2^о. При х₁<х₂, то Р{ х₁<X<х₂}= 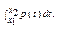3^о. 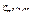=1(нормировочное св-во). График ф-ии плот-ти р(Х) наз-ют кривой распр. Площадь под крив. распр. =1.

Опр. Плот-тью совместного распр. двух непрер. сл. вел-н Х и Y, заданных на одном и томже вероят-ном простр-ве элемент-ых событий, наз-ся такая неотриц-ая ф-ия от двух переменных р(u, v), что "u, v верно рав-во Р{X<х, Y<y}=