Однородные СЛАУ. Фундаментальная система решений.

АХ=В – система и параллельно рассмотрим систему АХ=0. (АХ=В – Неоднородн. СЛАУ, АХ=0 – однородн. СДАУ).

Одновременно выполняется:

1. АХ=0 имеет тольок тривиальное решение, АХ=В имеет единственное решение или не имеет решений совсем.

2. АХ=0 имеет нетривиальное решение, АХ=В имеет бесконечное число решений.

Рассмотрим подробнее 2-ой случай: r(A) = r(A с волной сверху)<m..

M – r(A) – дефект, количество свободных неизвестных.

Пример:

,

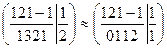б.м: х₁, х₂

св.м: х₃, х₄.

х₂ + х₃ +2х₄ = 1., х₂ = 1 – а – 2b, х₃ = а, х₄ = b.

х₁ = -2х₂ – х₃ + х₄ + 1 = -2 + 2а +4b – а + b+1 = -1 + а + 5b.

Ответ: (-1 + а + 5b., 1 – а – 2b , а, b)^Т.

Хо – общее решение ОСЛАУ

Х (с волной) – общее решение НСЛАУ

Векторы на плоскости и в пространстве. Операции над векторами.

Вектор– направленный отрезок, т.е. раз есть слово отрезок, значит есть начало и конец.

1. перенос отрезка при помощи параллельного переноса, не изменяет вектор.

2. вектор задается «длиной вектора» и направления.

3. если у вектора изменить направление на противоположное, то получаем противоположный вектор.

4. нулевой вектор – вектор, длина которого = 0 или начальная конечная точки совпадают. ( у нулевого вектора направление неопределенно).

Коллинеарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же прямой.

Примечание: если из двух коллинеарных векторов направление одинаковое, то вектора сонаправленные, а если противоположные, то называется противоположно-направленные.

Компланарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же плоскости.

Примечание: два вектора в пространстве всегда компланарны.

Примечание: два вектора называются равными, если они сонаправлены и равны по длине.

Линейные операции над векторами:

1. умножение вектора на число:

Результатом будет вектор, коллинеарный исходному (соноправленный в случае положительного множителя и противоположно-направленный – в случае отрицательного множителя), длина которого равна произведению модуля числового множителя на длину исходного модуля.

2. сумма двух векторов:

Есть вектор, получаемый из слагаемых при помощи правила параллелограмма или правила треугольника.

Коллинеарность и компланарность. Базис. Координаты.

Коллинеарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же прямой.

Примечание: если из двух коллинеарных векторов направление одинаковое, то вектора сонаправленные, а если противоположные, то называется противоположно-направленные.

Компланарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же плоскости.

Примечание: два вектора в пространстве всегда компланарны.

Примечание: два вектора называются равными, если они сонаправлены и равны по длине.

Базис пространства -совокупность лин независ векторов, по которым можно разложить любой вектор этого пр-ва.

Базис 3x мерного пр-ва образует любая тройка некомпланарных векторов пр-ва.

Если образуют базис в пространстве, то любой вектор из этого пространства может быть представлен: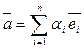

Примечание: для конкретно-заданного базиса не всегда просто бывает найти коэффициент .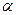

Проще всего это сделать когда базис является ортонормированным.

Понятие ортонормированности распадается на понятия ортогональности и нормированности.

( перпендикулярность и длина=1).

В 3-х мерном пространстве ортогональный базис состоит из 3 взаимноперпендикулярных векторов.

Ортонормированный базис состоит из 3-х взаимноперпендикулярных векторов, длина каждого из которых = 1.