Определитель матрицы, вычисление определителей, свойства определителей
ИКТИБ ИТА ЮФУ
КУРС ЛЕКЦИЙ ПО МАТЕМАТИКЕ
Лекция 4 Определитель матрицы, вычисление и свойства определителей
Что главное мы узнали на прошлой лекции
Мы узнали, что матрицей называется прямоугольная таблица чисел, изучили основные операции над матрицами.
Что мы узнаем на этой лекции
Матрица является одним из фундаментальных понятий математики. С помощью матриц строятся многие математические теории. На этой лекции мы изучим важную характеристику квадратной матрицы – ее определитель. В каком-то смысле можно провести параллель: число и модуль числа; квадратная матрица и ее определитель.
Определитель матрицы, вычисление определителей, свойства определителей
Важной характеристикой квадратной матрицы является ее определитель. В общем случае определение определителя очень сложное, поэтому мы вначале рассмотрим несколько частных случаев. Формально квадратная матрица может иметь размерность 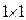 , т.е. быть квадратной матрицей 1-го порядка. В этом случае матрица состоит из одного элемента, и ее определитель равен самому этому элементу. Этот случай не является интересным, в приложениях нужны определители более высокого порядка.
, т.е. быть квадратной матрицей 1-го порядка. В этом случае матрица состоит из одного элемента, и ее определитель равен самому этому элементу. Этот случай не является интересным, в приложениях нужны определители более высокого порядка.
Рассмотрим квадратную матрицу  . Для записи определителя этой матрицы используются символы:
. Для записи определителя этой матрицы используются символы: 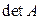 ,
,  .
.
Определение 1. Величина  называется определителем матрицы второго порядка
называется определителем матрицы второго порядка 
Итак, определитель матрицы второго порядка равен произведению элементов на главной диагонали минус произведение элементов на второй диагонали. Например: 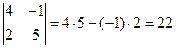 ,
, 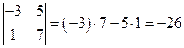 . Кстати, любопытно вспомнить, что это определители матриц
. Кстати, любопытно вспомнить, что это определители матриц  и
и 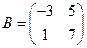 , для которых мы вычислили в предыдущей лекции их произведения в различном порядке:
, для которых мы вычислили в предыдущей лекции их произведения в различном порядке: 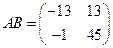 ,
,  . Заметим, что
. Заметим, что  и
и 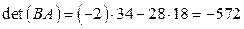 , т.е. в данном случае определитель произведения матриц равен произведению их определителей, т.к.
, т.е. в данном случае определитель произведения матриц равен произведению их определителей, т.к. 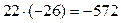 . Это свойство определителей матрицы будет справедливо всегда.
. Это свойство определителей матрицы будет справедливо всегда.
Отметим некоторые свойства определителей, которые несложно проверить для определителей второго порядка, и которые будут справедливы для определителей любого порядка.
Свойство 1. При транспонировании матрицы ее определитель не меняется, т.е.  .
.
В частности, 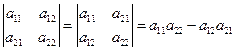 . Отсюда следует, что строки и столбцы определителя матрицы равноправны. Поэтому свойства определителей, сформулированные далее для строк, будут справедливы и для столбцов определителей.
. Отсюда следует, что строки и столбцы определителя матрицы равноправны. Поэтому свойства определителей, сформулированные далее для строк, будут справедливы и для столбцов определителей.
Свойство 2. Если поменять местами любые две строки определителя, то он поменяет знак.
Для определителей второго порядка это очевидно  .
.
Свойство 3. Если все элементы строки определителя умножить на одно и то же число, то и сам определитель умножится на это число.
В частности, 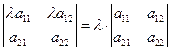 .
.
Свойство 4. Если две строки определителя равны или пропорциональны, то определитель равен 0.
Проверьте, что свойство 4 является прямым следствием свойств 2 и 3.
Свойство 5. Если строка определителя равны сумме двух строк, то определитель равен сумме определителей с этими строками.
Давайте расшифруем это свойство:  .
.
Свойство 6. Если к одной из строк определителя прибавить другую строку, умноженную на число 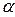 , то определитель не изменится.
, то определитель не изменится.
Это свойство означает следующее: 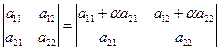 . В данном случае мы к первой строке определителя второго порядка прибавили вторую, умноженную на число
. В данном случае мы к первой строке определителя второго порядка прибавили вторую, умноженную на число 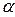 .
.
Свойство 7. Определитель произведения матриц равен произведению их определителей.
Выясним теперь, что такое определитель 3-го порядка. Рассмотрим квадратную матрицу  , порядок которой равен
, порядок которой равен 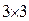 или просто 3.
или просто 3.
Определение 2. Определителем матрицы третьего порядка называется величина
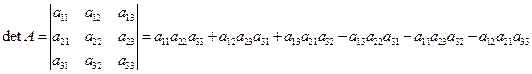 . (1)
. (1)
На первый взгляд, в этой формуле трудно найти закономерность. Заучивать ее, быстрее всего, бесполезно, поэтому давайте подметим несколько закономерностей. Для формального запоминания действий можно






 представить себе заданный определитель 3-го
представить себе заданный определитель 3-го
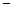
 + + + порядка, у которого повторены 1 и 2 столбцы.
+ + + порядка, у которого повторены 1 и 2 столбцы.
Произведение элементов, идущих из левого верхнего угла к правому нижнему, берутся со знаком +. Произведение элементов, идущих из правого верхнего угла к левому нижнему, берутся со знаком 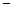 .
.
Отметим еще 1 способ запомнить формулу (1), для чего проверьте справедливость равенства 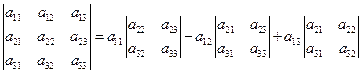 .
.
Определение 3. Пусть в определителе выделены 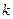 строк и
строк и 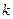 столбцов. Элементы, принадлежащие одновременно выделенным строкам и столбцам, стоящие в том же порядке, образуют определитель, который называется минором
столбцов. Элементы, принадлежащие одновременно выделенным строкам и столбцам, стоящие в том же порядке, образуют определитель, который называется минором 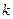 –го порядка заданного определителя и обозначается
–го порядка заданного определителя и обозначается  .
.
Определение 4. Пусть в определителе выделен элемент 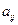 , стоящий на пересечении
, стоящий на пересечении 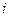 -й строки и
-й строки и 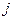 -го столбца. Элементы, не принадлежащие этой строке и этому столбцу, стоящие в том же порядке, образуют определитель, который называется минором, соответствующему элементу
-го столбца. Элементы, не принадлежащие этой строке и этому столбцу, стоящие в том же порядке, образуют определитель, который называется минором, соответствующему элементу 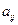 заданного определителя. Этот минор обозначается символом
заданного определителя. Этот минор обозначается символом 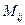 .
.
Определение 5. Пусть в определителе выделен элемент 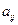 , стоящий на пересечении
, стоящий на пересечении 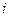 -й строки и
-й строки и 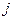 -го столбца. Алгебраическим дополнением, соответствующему элементу
-го столбца. Алгебраическим дополнением, соответствующему элементу 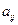 заданного определителя, называется величина, равная
заданного определителя, называется величина, равная  . Это алгебраическое дополнение обозначается символом
. Это алгебраическое дополнение обозначается символом 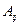 .
.
Таким образом, справедлива формула 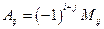 .
.
Определение 6. Определителем называется сумма попарных произведений элементов первой строки на их алгебраические дополнения.
С учетом определения 2, следствия из него и определения 5 справедливо следующее свойство.
Свойство 8. Определитель равен сумме попарных произведений элементов любой строки или столбца на их алгебраические дополнения.
Например, для определителя 3-го порядка справедливы формула  . Кроме того, используя свойство 8, убедитесь в справедливости следующего свойства.
. Кроме того, используя свойство 8, убедитесь в справедливости следующего свойства.
Свойство 9. Определитель матрицы треугольного вида равен произведению элементов на главной диагонали.
Пример 1. Вычислите определители матриц  ,
, 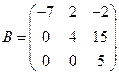 ,
, 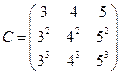 ,
, 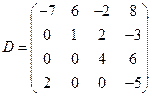 .
.
Решение.
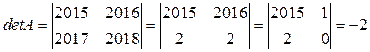 ,
,
 ,
,
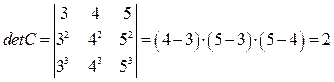 ,
,
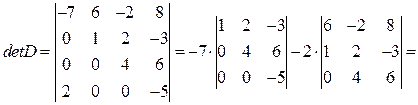
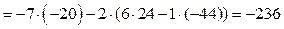 .
.
Вычисление определителей является важной операцией, необходимой во многих приложениях. Как мы видим, несложно вычислить определитель второго и третьего порядков. Для этого достаточно использовать определения определителя. Можно проверить, что для вычисления таким способом определителя  -го порядка потребуется примерно
-го порядка потребуется примерно 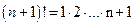 арифметических операций. При
арифметических операций. При 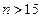 это будет не под силу даже суперкомпьютеру. Поэтому для вычисления «серьезного» определителя его, используя свойства, приводят к треугольному виду и используют свойство 9.
это будет не под силу даже суперкомпьютеру. Поэтому для вычисления «серьезного» определителя его, используя свойства, приводят к треугольному виду и используют свойство 9.
