Способы задания функции
Наиболее часто используются следующие способы задания функции: 1) аналитический, 2) графический; 3) при помощи таблицы; 4) при помощи словесного описания.
В общем случае всякий закон, определяющий функцию 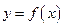 , задается некоторым текстом. Наиболее распространенная форма такого текста – формула, позволяющая вычислять значение функции
, задается некоторым текстом. Наиболее распространенная форма такого текста – формула, позволяющая вычислять значение функции 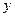 по заданному значению аргумента
по заданному значению аргумента  . Способ задания функции с помощью формул называется аналитическим.
. Способ задания функции с помощью формул называется аналитическим.
Аналитический способ, в свою очередь, подразделяется на три способа: явный, неявный и параметрический.
Явный способ – это непосредственное выражение зависимой переменной через независимую переменную в виде формулы 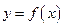 :
: 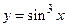 ,
, 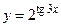 и т.п.
и т.п.
Неявный способ. Пусть дано уравнение вида 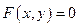 и пусть существует такое множество
и пусть существует такое множество 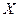 , что для каждого
, что для каждого 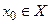 определено, по крайней мере, одно число
определено, по крайней мере, одно число 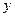 , удовлетворяющее уравнению
, удовлетворяющее уравнению 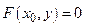 . Обозначим одно из таких чисел через
. Обозначим одно из таких чисел через 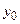 и поставим его в соответствие числу
и поставим его в соответствие числу 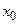 . В результате имеем функцию
. В результате имеем функцию 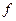 , которая осуществляет это соответствие, определенную на множестве
, которая осуществляет это соответствие, определенную на множестве 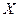 , и такую, что
, и такую, что 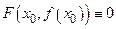 для всех
для всех 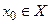 . В этом случае говорят, что функция
. В этом случае говорят, что функция 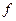 задается неявно уравнением
задается неявно уравнением 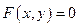 . Уравнение
. Уравнение 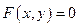 может определять не одну функцию, а некоторое множество неявно заданных функций.
может определять не одну функцию, а некоторое множество неявно заданных функций.
Примеры. а) Из уравнения 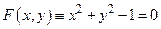 следует
следует 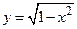 и
и 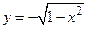 , т.е данное уравнение задает неявно две функции.
, т.е данное уравнение задает неявно две функции.
б) Из уравнения 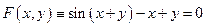 невозможно получить ни аналитическую зависимость
невозможно получить ни аналитическую зависимость 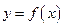 , ни зависимость
, ни зависимость 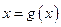 .
.
Параметрический способ задания функции – это выражения зависимой и независимой переменных через третью переменную, называемую параметром:
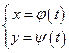 ,
, 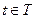 ,
,
где 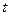 – параметр,
– параметр, 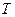 – область определения функций
– область определения функций 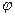 и
и 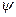 (область изменения параметра
(область изменения параметра 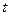 ).
).
Замечание. Если рассматривать 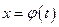 как уравнение для определения
как уравнение для определения 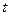 , из которого можно получить
, из которого можно получить 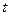 как функцию от
как функцию от  :
: 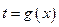 , то подставляя в функцию
, то подставляя в функцию 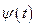 вместо
вместо 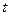 его выражение через
его выражение через  , получим явное задание
, получим явное задание 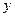 от
от  в виде
в виде 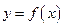 .
.
Пример. Функция 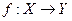 задана параметрически:
задана параметрически: 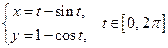 .
.
Когда параметр 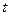 принимает значения из
принимает значения из 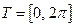 ,
,  принимает значения из множества
принимает значения из множества 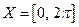 , а
, а 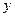 – из множества
– из множества 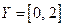 . Решить уравнение
. Решить уравнение 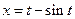 относительно
относительно 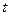 невозможно (нельзя явно выразить
невозможно (нельзя явно выразить 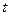 через
через  ), а потому нельзя получить явную зависимость
), а потому нельзя получить явную зависимость 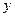 от
от  в виде
в виде 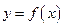 .
.
При табличном способе задания функции «текст», задающий соответствие 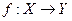 , «записывается» в виде таблицы, в которой в одной строке расписываются значения аргумента, а в другой строке – соответствующие значения функции.
, «записывается» в виде таблицы, в которой в одной строке расписываются значения аргумента, а в другой строке – соответствующие значения функции.
Напомним графический способ задания функции. Введем на плоскости прямоугольную систему координат. Пусть 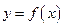 – числовая функция с областью определения
– числовая функция с областью определения 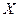 , тогда график функции есть множество точек плоскости
, тогда график функции есть множество точек плоскости  с координатами
с координатами 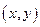 , где
, где 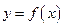 ,
, 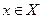 (т.е. множество точек с координатами
(т.е. множество точек с координатами 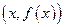 ). Строго говоря, точное построение графика функции невозможно, так как любое геометрическое изображение точек, отрезков, кривых и других объектов можно сделать только приближенно, поэтому рисунок, на самом деле, является только эскизом графика. Однако, если кривая построена достаточно точно, то ее также называют графиком функции. График функции более наглядно отражает такие качественные характеристики функций как монотонность, выпуклость вверх и вниз, наличие асимптот (более подробно эти характеристики будут рассмотрены ниже).
). Строго говоря, точное построение графика функции невозможно, так как любое геометрическое изображение точек, отрезков, кривых и других объектов можно сделать только приближенно, поэтому рисунок, на самом деле, является только эскизом графика. Однако, если кривая построена достаточно точно, то ее также называют графиком функции. График функции более наглядно отражает такие качественные характеристики функций как монотонность, выпуклость вверх и вниз, наличие асимптот (более подробно эти характеристики будут рассмотрены ниже).
