Линейные уравнения с постоянными коэффициентами
Чтобы решить линейное однородное уравнение с постоянными коэффициентами
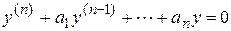 , (2.4)
, (2.4)
надо составить характеристическое уравнение
 (2.5)
(2.5)
и найти его корни 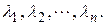
Общее решение уравнения (2.4) есть линейная комбинация слагаемых вида 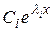 для каждого простого корня
для каждого простого корня 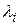 уравнения (2.5) и слагаемых вида
уравнения (2.5) и слагаемых вида
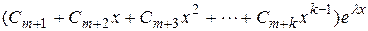
для каждого корня 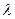 уравнения (2.5) кратности
уравнения (2.5) кратности 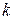 . Все
. Все  – произвольные постоянные. Корни характеристического уравнения могут быть как действительными, так и комплексными числами.
– произвольные постоянные. Корни характеристического уравнения могут быть как действительными, так и комплексными числами.
Если все коэффициенты уравнения (2.4) вещественные, то его решение всегда может быть записано в вещественной форме даже в случае комплексных корней уравнения (2.5). Для каждой пары комплексно-сопряженных корней 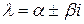 характеристического уравнения в формулу общего решения включаются слагаемые
характеристического уравнения в формулу общего решения включаются слагаемые 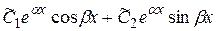 , если эти корни простые, и слагаемые
, если эти корни простые, и слагаемые 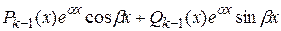 , если каждый из комплексных корней имеет кратность
, если каждый из комплексных корней имеет кратность  . Здесь
. Здесь 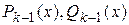 – многочлены степени
– многочлены степени 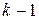 , коэффициенты которых – произвольные постоянные.
, коэффициенты которых – произвольные постоянные.
Пример. Найти общее решение уравнения
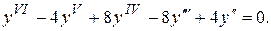
Решение. Составляем характеристическое уравнение и находим его корни. Имеем
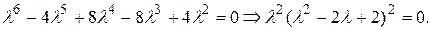
Откуда  Поэтому общее решение уравнения имеет вид
Поэтому общее решение уравнения имеет вид
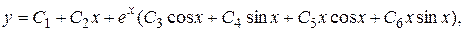
где 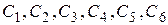 – произвольные постоянные.
– произвольные постоянные.
Общее решение линейного неоднородного уравнения
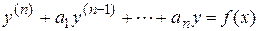 (2.6)
(2.6)
имеет вид  , где
, где 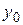 – общее решение соответствующего однородного уравнения (24), а
– общее решение соответствующего однородного уравнения (24), а 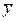 – какое-либо частное решение неоднородного уравнения (2.6).
– какое-либо частное решение неоднородного уравнения (2.6).
Для уравнения (2.6) с постоянными коэффициентами 
и правой частью  специального вида, то есть состоящей из сумм и произведений функций
специального вида, то есть состоящей из сумм и произведений функций  частное решение
частное решение  можно искать методом неопределенных коэффициентов.
можно искать методом неопределенных коэффициентов.
Для уравнений с правой частью вида
 , (2.7)
, (2.7)
где 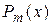 – многочлен степени
– многочлен степени  , частное решение имеет вид
, частное решение имеет вид  . Здесь
. Здесь 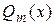 – многочлен той же степени
– многочлен той же степени  , а
, а  , если
, если 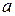 не является корнем характеристического уравнения (2.5), если же
не является корнем характеристического уравнения (2.5), если же 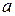 – корень характеристического уравнения, то
– корень характеристического уравнения, то  – его кратность. Чтобы найти коэффициенты многочлена
– его кратность. Чтобы найти коэффициенты многочлена 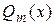 , нужно подставить в уравнение (2.6) значение
, нужно подставить в уравнение (2.6) значение  и его производных и приравнять коэффициенты при подобных членах в левой и правой частях получившегося равенства.
и его производных и приравнять коэффициенты при подобных членах в левой и правой частях получившегося равенства.
Для уравнения с правой частью вида
 (2.8)
(2.8)
можно искать частное решение в виде 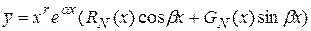 , где
, где 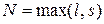 , а
, а  , если
, если 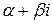 не является корнем характеристического уравнения (2.5) и
не является корнем характеристического уравнения (2.5) и  равно кратности этого корня в противном случае.
равно кратности этого корня в противном случае.
Если правая часть уравнения представляет собой сумму 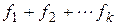 функций вида (2.7) и (2.8), то частное решение ищется в виде суммы
функций вида (2.7) и (2.8), то частное решение ищется в виде суммы 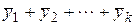 , где
, где  – частное решение уравнения (2.6) с
– частное решение уравнения (2.6) с 
Пример.Найти общее решение уравнения
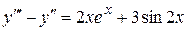 .
.
Решение.Характеристическое уравнение  имеет корни
имеет корни 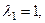
 . Поэтому общее решение однородного уравнения имеет вид
. Поэтому общее решение однородного уравнения имеет вид 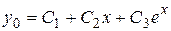 . Частное решение неоднородного уравнения представляет собой сумму
. Частное решение неоднородного уравнения представляет собой сумму 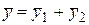 , где
, где 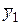 – частное решение уравнения
– частное решение уравнения
 , (2.9)
, (2.9)
а  – частное решение уравнения
– частное решение уравнения
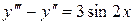 . (2.10)
. (2.10)
Так как число 1 является корнем характеристического уравнения, то 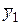 будем искать в виде
будем искать в виде 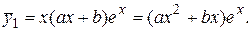 Подставив в уравнение (2.9) выражения для
Подставив в уравнение (2.9) выражения для 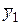 и его производных и приведя подобные члены, получим
и его производных и приведя подобные члены, получим
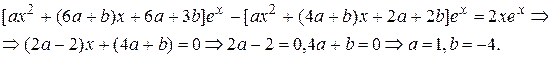
Итак, 
Поскольку числа  не являются корнями характеристического уравнения, то
не являются корнями характеристического уравнения, то  будем искать в виде
будем искать в виде 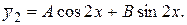 Подставив в уравнение (2.10) выражения для
Подставив в уравнение (2.10) выражения для 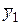 и его производных и приведя подобные члены, получим
и его производных и приведя подобные члены, получим
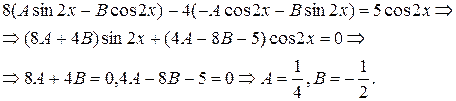
Итак, 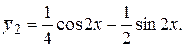
Окончательно получаем
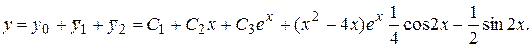
Частное решение линейного уравнения (2.6) с произвольной правой частью может быть найдено методом вариации произвольных постоянных.
Пусть найдено общее решение  линейного однородного уравнения (2.4). Тогда частное решение неоднородного уравнения (2.6) ищется в виде
линейного однородного уравнения (2.4). Тогда частное решение неоднородного уравнения (2.6) ищется в виде 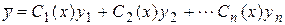 . Функции
. Функции  определяются из системы
определяются из системы
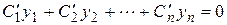
 (2.11)
(2.11)
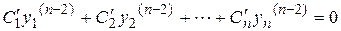
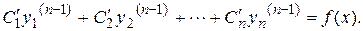
Пример. Найти общее решение уравнения 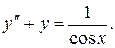
Решение. Соответствующее однородное уравнение имеет вид  Корни его характеристического уравнения
Корни его характеристического уравнения 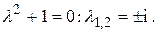 Поэтому общее решение однородного уравнения
Поэтому общее решение однородного уравнения  Общее решение неоднородного уравнения будем искать в виде
Общее решение неоднородного уравнения будем искать в виде  Для нахождения производных функций
Для нахождения производных функций  запишем систему (2.11):
запишем систему (2.11):

Решив эту систему, получим 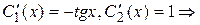
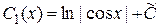 ,
, 
Итак, общее решение данного уравнения имеет вид
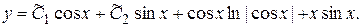
Здесь  – частное решение исходного неоднородного уравнения.
– частное решение исходного неоднородного уравнения.
Задание 8
Найти общее решение дифференциального уравнения
1. 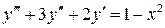
2. 
3. 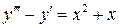
4. 
5. 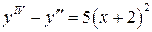
6. 
7. 
8. 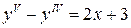
9. 
10. 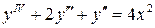
11. 
12. 
13. 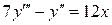
14. 
15. 
16. 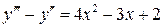
17. 
18. 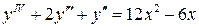
19. 
20. 
21. 
22. 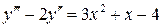
23. 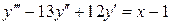
24. 
25. 
26. 
27. 
28. 
29. 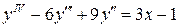
30. 
31. 
Задание 9
Найти общее решение дифференциального уравнения
1. 
2. 
3. 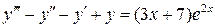
4. 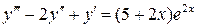
5. 
6. 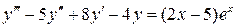
7. 
8. 
9. 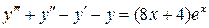
10. 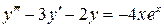
11. 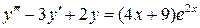
12. 
13. 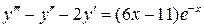
14. 
15. 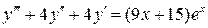
16. 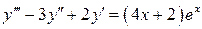
17. 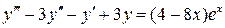
18. 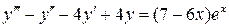
19. 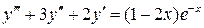
20. 
21. 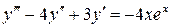
22. 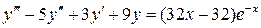
23. 
24. 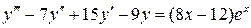
25. 
26. 
27. 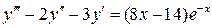
28. 
29. 
30. 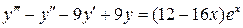
31. 
Задание 10
Найти общее решение дифференциального уравнения
1. 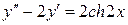
2. 
3. 
4. 
5. 
6. 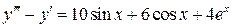
7. 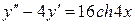
8. 
9. 
10. 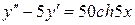
11. 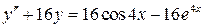
12. 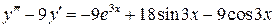
13. 
14. 
15. 
16. 
17. 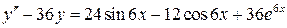
18. 
19. 
20. 
21. 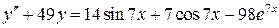
22. 
23. 
24. 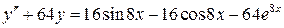
25. 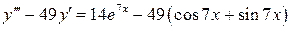
26. 
27. 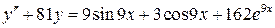
28. 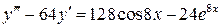
29. 
30. 
31. 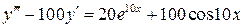
Задание 11
Найти решение задачи Коши
1. 
2. 
3. 
4. 
5. 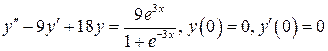
6. 
7. 
8. 
9. 
10. 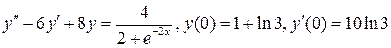
11. 
12. 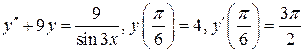
13. 
14. 
15. 
16. 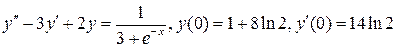
17. 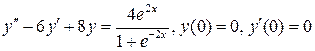
18. 
19. 
20. 
21. 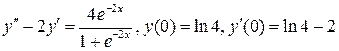
22. 
23. 
24. 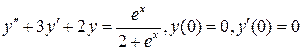
25. 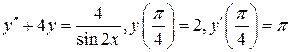
26. 
27. 
28. 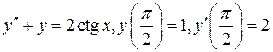
29. 
30. 
31. 
