V – зависимая переменная

Тема: «Функции, их свойства и графики. Степенная функция»

Степени. Корни.

Определения степеней:

1. a ⁿ = a ×a × …×a, n Î N.

2. a¹ = a

3. а ⁰ = 1 , 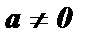(0 ⁰ - не имеет смысла).

4. , .

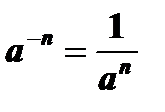5. , a ³ 0, n Î N, т Î Z.

Свойства степеней:

Четная степень отрицательного числа есть число положительное.

Нечетная степень отрицательного числа есть число отрицательное.

Любая степень положительного числа есть число положительное.

4. 0 ⁿ = 0, nÎ N .

5. 1 ⁿ = 1 , nÎ N .

6. .

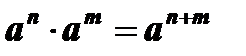7. .

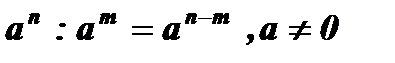8. .

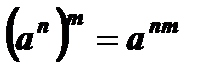9. .

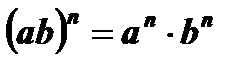10. .

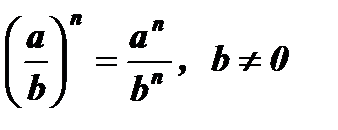Определения корней:

1. .

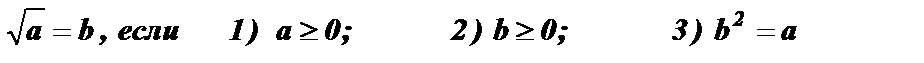2.

Свойства корней:

1. 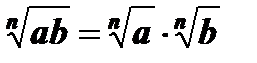, а ³ 0, b ³ 0.

2. 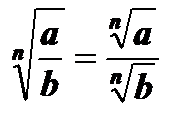, а ³ 0, b > 0.

3. , а ³ 0, nÎ N, kÎ N.

4. , а ³ 0, nÎ N, тÎ N.

5. 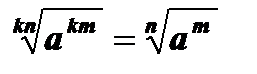, а ³ 0, nÎ N, тÎ N , kÎ N.

6. При любом значении а .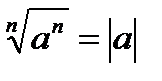

2. Числовая функция: область определения, множество значений, способы задания

Применение математики к изучению законов природы и к использованию их в технике заставило ввести в математику понятия постоянной и переменной величин. Все величины, изучаемые в математике, делятся на постоянные и переменные.

Определение: Величина называется постоянной, если она в условиях данного эксперимента сохраняет одно и то же значение.

(Постоянная – const. (лат.))

Пример: Постоянными величинами являются:

1. длина радиуса данной окружности;

Температура кипения воды при постоянном давлении.

Замечание: Некоторые постоянные сохраняют свое числовое значение при любых условиях, их называют абсолютными постоянными.

Пример: Абсолютными постоянными величинами являются:

1. сумма углов треугольника;

2. скорость света в пустоте;

3. количество секунд в минуте;

4. p = 3,14…;

5. е = 2,718281828459045… .

Определение: Величина называется переменной, если она в условиях данного эксперимента может принимать различные значения.

Пример: Скорость камня, брошенного вверх, является переменной величиной.

В практических задачах часто рассматриваются переменные величины, которые связаны между собой так, что значения одной определяют значения другой.

Пример: Объем V шара радиуса R определяется по формуле .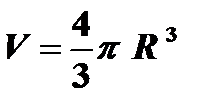

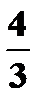; p – постоянные величины;

R – независимая переменная;

V – зависимая переменная.

Определение: Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.

х – независимая переменная, аргумент;

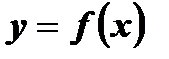– зависимая переменная, значение функции;

Пример: V = f ( R ) – объем является функцией радиуса, то есть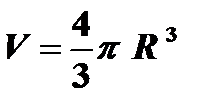

Определение: Областью определения функции называются все значения аргумента x, при которых функция определена (то есть имеет числовое значение).

D ( f ) = Х – область определения функции.

Определение: Множеством значений функции называются все значения зависимой переменной y при x из области определения функции.

E ( f ) = У – множество значений функции.

Пример: Найти область определения функции:

1.

При любом действительном значении х функция у так же выражается действительным числом, следовательно, функция определена при любом значении . Следовательно, .

2.

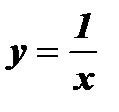
Знаменатель дроби обращается в нуль при х = 0. Функция принимает действительные значения при всех х , кроме х = 0. Следовательно,

.

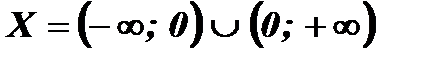3.

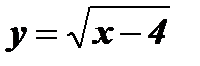
Функция имеет смысл только в том случае, когда подкоренное выражение больше нуля или равно нулю (неотрицательное), то есть . Следовательно, .

Замечание:

1. При нахождении области определения дробной функции нужно исключить значения аргумента, при которых знаменатель дроби обращается в нуль. Для этого знаменатель дроби приравнивается к нулю. Если полученное уравнение имеет корни, то они исключаются из области определения функции.

2. Если функция содержит корень четной степени, то при нахождении области определения нужно исключить значения аргумента, при которых подкоренное выражение принимает отрицательные значения. В область определения функции войдут значения аргумента, при которых подкоренное выражение принимает неотрицательные значения, то есть решения соответствующего неравенства.