Образец выполнения задания № 4
Полярная система координат определяется заданием некоторой точки 0, называемой полюсом, лучом Oр, называемым полярной осью и единицы масштаба ОЕ.
Полярными координатами точки М называются: расстояние r = 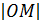 - полярный радиус, полярный угол
- полярный радиус, полярный угол  между полярной осью и лучом Ор. Полярный угол имеет бесконечное множество значений, главное его значение удовлетворяет условию 0
между полярной осью и лучом Ор. Полярный угол имеет бесконечное множество значений, главное его значение удовлетворяет условию 0 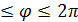 (рис. 4).
(рис. 4).
Обозначается М(r;  ).
).
При совпадении полюса и начала декартовой системы координат, направлений полярной оси и оси абсцисс связь между прямоугольными и декартовыми координатами выражается формулами:
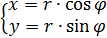 и, обратно, r =
и, обратно, r = 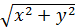 , tg
, tg 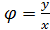 .
.
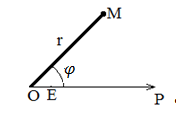
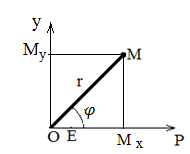
Рис.4
Задача.Дано уравнение 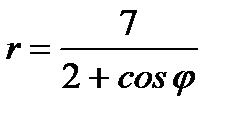 линии в полярной системе координат. Надо: 1) определить точки, лежащие на линии, давая
линии в полярной системе координат. Надо: 1) определить точки, лежащие на линии, давая 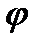 значения через промежуток, равный
значения через промежуток, равный  , начиная от
, начиная от 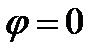 в промежутке
в промежутке 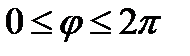 ; 2) построить линию, соединив полученные точки с помощью лекала или от руки; 3) найти уравнение этой линии в прямоугольной декартовой системе координат (положительная полуось абсцисс берется совпадающей с полярной осью, полюс – с началом прямоугольной декартовой системы координат; обе системы координат берутся правыми); 4) определить вид кривой.
; 2) построить линию, соединив полученные точки с помощью лекала или от руки; 3) найти уравнение этой линии в прямоугольной декартовой системе координат (положительная полуось абсцисс берется совпадающей с полярной осью, полюс – с началом прямоугольной декартовой системы координат; обе системы координат берутся правыми); 4) определить вид кривой.
Решение.1) Для построения кривой, заданной уравнением 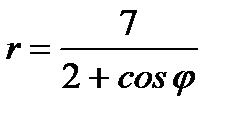 , придаем
, придаем 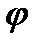 значения от
значения от 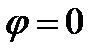 до
до  через промежуток (с шагом)
через промежуток (с шагом)  и заносим полученные значения в таблицу.
и заносим полученные значения в таблицу.
Для получения таблицы в Excel в ячейку A1 вводится текст «Расчетная таблица», в ячейку C1 – «Таблица исходных данных». Выделяется диапазон ячеек A1:B1, выводится Формат ячеек, на вкладке Выравнивание выбирается выравнивание по центру по вертикале и по горизонтали, устанавливаются флажки Перенос по словам и Объединение ячеек. Во 2 строку вводится название координат  и r, диапазон значений
и r, диапазон значений  0,
0,  n, шаг h.
n, шаг h.
В ячейку A3 вводится формула =$C$2 абсолютной ссылки на левую границу отрезка.
В ячейку A4 вводится формула =A3+$E$2 изменения значения аргумента функции  на шаг h. Копируется формулу из ячейки A4 до ячейки A19. В ячейку B3 вводится формула вычисления кривой =7/(2+COS(A4)). Копируется формула из ячейки B3 до B19 (рис. 5).
на шаг h. Копируется формулу из ячейки A4 до ячейки A19. В ячейку B3 вводится формула вычисления кривой =7/(2+COS(A4)). Копируется формула из ячейки B3 до B19 (рис. 5).

Рис. 5
2)Для построения в полярной системе координат в произвольной точке плоскости определяем полюс О, полярную ось Ор, единичный отрезок ОЕ, из полюса проводим лучи с шагом h =  :
: 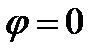 (полярная ось),
(полярная ось), 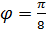 ,
, 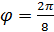 ,
, 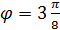 , …,
, …, 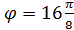 . На каждом луче откладываем соответствующие значения полярного радиуса r, соединяем последовательно точки с координатами
. На каждом луче откладываем соответствующие значения полярного радиуса r, соединяем последовательно точки с координатами 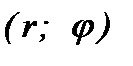 , получаем кривую (рис. 6).
, получаем кривую (рис. 6).
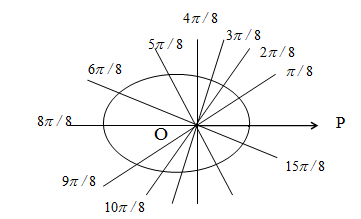
Рис. 6
В системе Mathematica таблицу значений угла 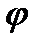 , полярного радиуса
, полярного радиуса  , построение графика функции
, построение графика функции 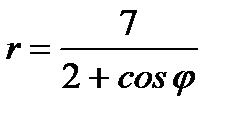 в полярной системе координат можно рассмотреть на рис.7.
в полярной системе координат можно рассмотреть на рис.7.
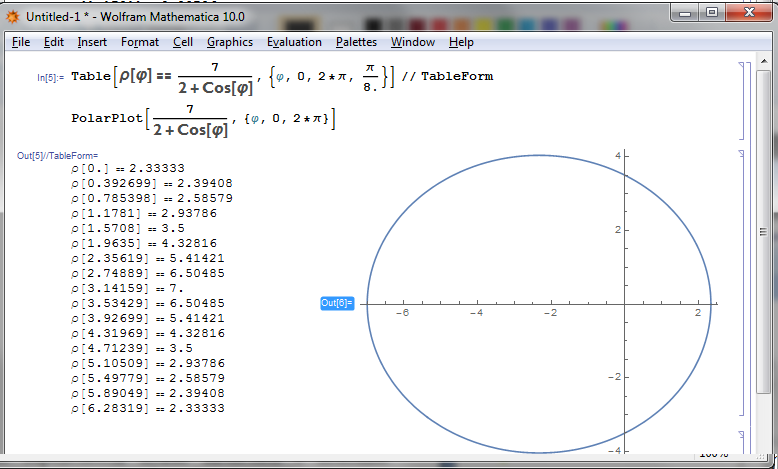
Рис. 7
3) Для получения уравнения линии в прямоугольной системе координат подставим значения полярного радиуса  и угла
и угла 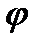 , связывающие полярную и прямоугольную системы координат.
, связывающие полярную и прямоугольную системы координат.
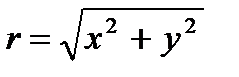 ,
,  ,
, 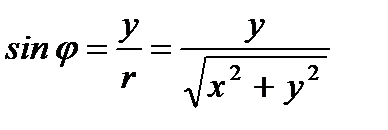 .
.
Тогда 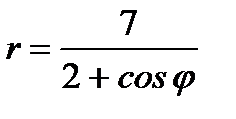



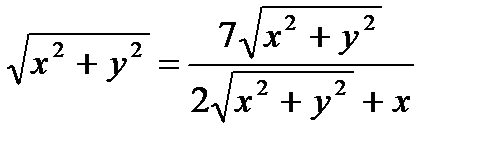

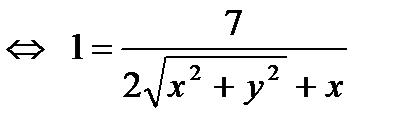

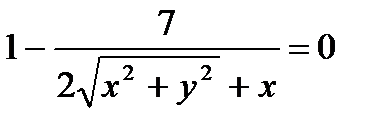



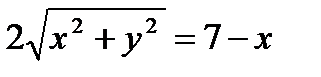

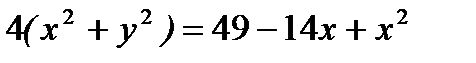

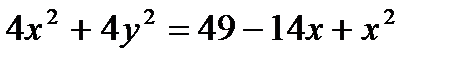


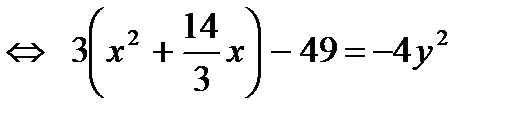



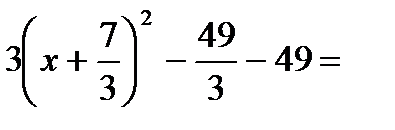
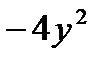



 .
.
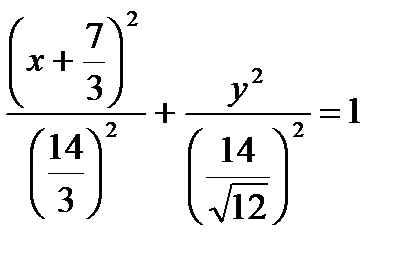 - уравнение эллипса с центром в точке
- уравнение эллипса с центром в точке  и полуосями
и полуосями 
Напомним, что полярный радиус точки может принимать только неотрицательные значения.
Задания к контрольной работе №1
Задание № 1
Заданы уравнения трех плоскостей. Требуется найти координаты точек их пересечения: 1)по формулам Крамера, 2) методом Гаусса.
1. 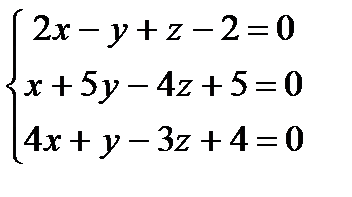 2.
2. 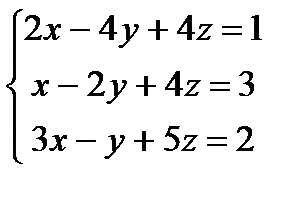
3.  4.
4. 
5. 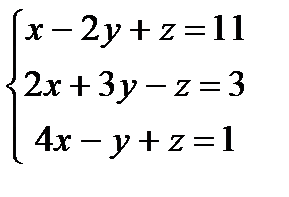 6.
6. 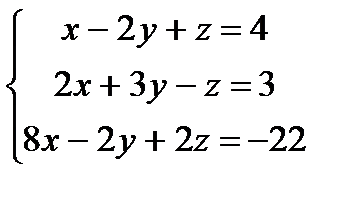
7. 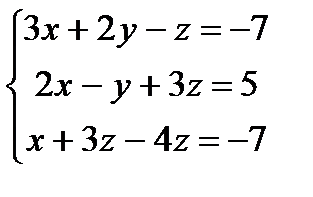 8.
8. 
9.  10.
10. 
11. 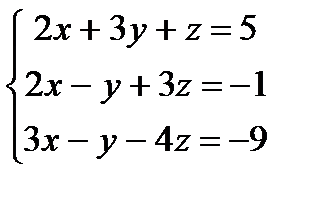 12.
12. 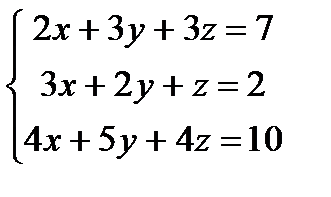
13.  14.
14. 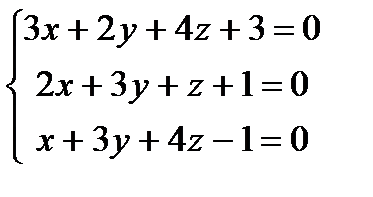
15. 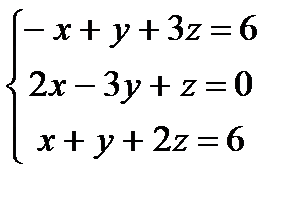 16.
16. 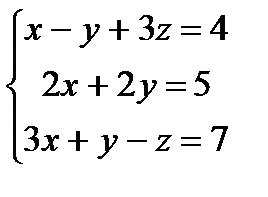
17.  18.
18. 
19. 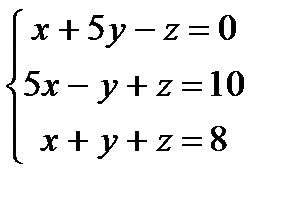 20.
20. 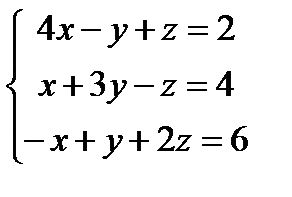
21.  22.
22. 
23.  24.
24. 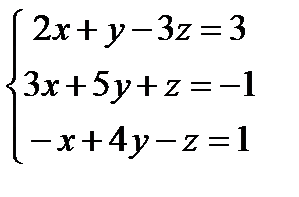
25. 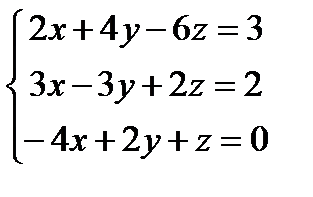
26. 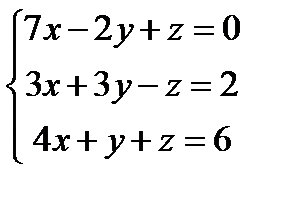
27. 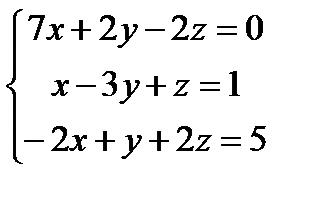
28. 
29. 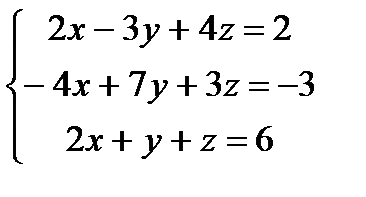 30.
30. 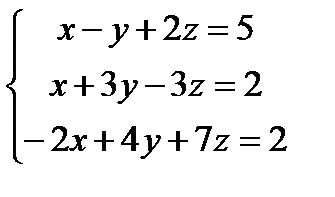
Задание №2
Даны координаты вершин пирамиды 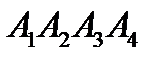 .Средствами векторной алгебры найти: Найти: a) угол между векторами
.Средствами векторной алгебры найти: Найти: a) угол между векторами  и
и 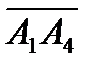 ;
;
б) площадь грани  ;
;
в) объем пирамиды;
г) уравнение плоскости (А1А2А3)
д) длину высоты, опущенной из вершины 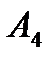 на грань
на грань  ;
;
е) длину медианы 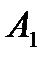 к ребру А3А4 грани А1А3А4.
к ребру А3А4 грани А1А3А4.
1. А1(1,3,6); А2(2,2,1); А3(-1,0,1); А4(-4,6,-3)
2. А1(-4,2,6); А2(2,-3,0); А3(-10,5,8); А4(-5,2,-4).
3. А1(7,2,4); А2(7,-1,-2); А3(3,3,1); А4(-4,2,1).
4. А1(2,1,4); А2(-1,5,-2); А3(-7,-3,2); А4(-6,-3,6).
5. А1(-1,-5,2); А2(-6,0,-3); А3(3,6,-3); А4(-10,6,7).
6. А1(0,-1,-1); А2(-2,3,5); А3(1,-5,-9); А4(-1,-6,3).
7. А1(5,2,0); А2(2,5,0); А3(1,2,4); А4(-1,1,1).
8. А1(2,-1,-2); А2(1,2,1); А3(5,0,-6); А4(-10,9,-7).
9. А1(-2,0,-4); А2(-1,7,1); А3(4,-8,-4); А4(1,-4,6).
10. А1(14,4,5); А2(-5,-3,2); А3(-2,-6,-3); А4(-2,2,-1).
11. А1(1,2,0); А2(3,0,-3); А3(5,2,6); А4(8,4,-9).
12. А1(2,-1,2); А2(1,2,-1); А3(3,2,1); А4(-4,2,5).
13. А1(1,1,2); А2(-1,1,3); А3(2,-2,4); А4(-1,0,-2).
14. А1(2,3,1); А2(4,1,-2); А3(6,3,7); А4(7,5,-3).
15. А1(1,1,-1); А2(2,3,1); А3(3,2,1); А4(5,9,-8).
16. А1(1,5,-7); А2(-3,6,3); А3(-2,7,3); А4(-4,8,-12).
17. А1(-3,4,-7); А2(1,5,-4); А3(-5,-2,0); А4(2,5,4).
18. А1(-1,2,-3); А2(4,-1,0); А3(2,1,-2); А4(3,4,5).
19. А1(4,-1,3); А2(-2,1,0); А3(0,-5,1); А4(3,2,-6).
20. А1(1,-1,1); А2(-2,0,3); А3(2,1,-1); А4(2,-2,-4).
21. А1(1,2,0); А2(1,-1,2); А3(0,1,-1); А4(-3,0,1).
22. А1(1,0,2); А2(1,2,-1); А3(2,-2,1); А4(2,1,0).
23. А1(1,2,-3); А2(1,0,1); А3(-2,-1,6); А4(0,-5,-4).
24. А1(3,10,-1); А2(-2,3,-5); А3(-6,0,-3); А4(1,-1,2).
25. А1(-1,2,4); А2(-1,-2,-4); А3(3,0,-1); А4(7,-3,1).
26. А1(0,-3,1); А2(-4,1,2); А3(2,-1,5); А4(3,1,-4).
27. А1(1,3,0); А2(4,-1,2); А3(3,0,1); А4(-4,3,5).
28. А1(-2,-1,-1); А2(0,3,2); А3(3,1,-4); А4(-4,7,3).
29. А1(-3,-5,6); А2(2,1,-4); А3(0,-3,-1); А4(-5,2,-8).
30. А1(2,-4,-3); А2(5,-6,0); А3(-1,3,-3); А4(-10,-8,7).
Задание № 3
1. Построить окружность 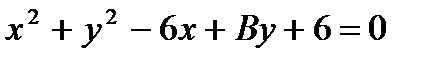 , проходящую через точку M (3;-3).
, проходящую через точку M (3;-3).
2. Составить уравнение окружности, диаметром которой служит отрезок прямой  , заключенный между осями координат.
, заключенный между осями координат.
3. Найти площадь треугольника, вершина которого лежит в центре окружности  , а основание вырезано окружностью на оси абсцисс.
, а основание вырезано окружностью на оси абсцисс.
4. Через центры окружностей 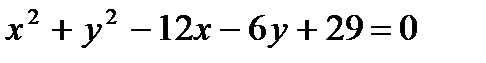 и
и 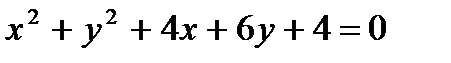 проведена прямая до пересечения её с осью абсцисс. Найти угол, образованный этой прямой с осью Оx.
проведена прямая до пересечения её с осью абсцисс. Найти угол, образованный этой прямой с осью Оx.
5. Найти уравнение касательной окружностей 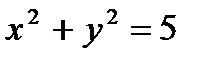 в точке M(1;-2).
в точке M(1;-2).
6. Найти уравнение прямой, проходящей через центр окружности  , перпендикулярной биссектрисе I и III координат углов.
, перпендикулярной биссектрисе I и III координат углов.
7. Написать уравнение эллипса, если его малая ось равна 10, а эксцентриситет  .
.
8. Найти угол между прямыми, соединяющими фокусы эллипса 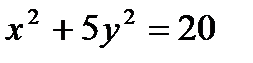 с точкой пересечения прямых
с точкой пересечения прямых 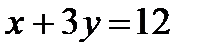 и
и 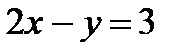 .
.
9. Определить вид кривой  и построить график.
и построить график.
10. Определить вид кривой 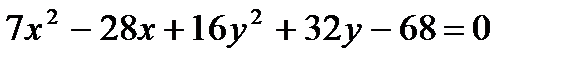 и построить её.
и построить её.
11. Найти уравнение геометрического места центров окружностей, касающихся оси абсцисс и проходящих через точку А(0; 3).
12. Найти уравнение геометрического места точек, каждая из которых вдвое ближе к точке А(1; 0), чем к точке В(-2; 0).
13. Найти уравнение геометрического места точек, для которых отношение расстояния до начала координат к расстоянию до прямой 3х+16=0 равно 0,6.
14. Найти уравнение геометрического места точек, каждая из которых находится вдвое дальше от точки А(3; 0), чем от оси ординат.
15. Найти уравнение геометрического места точек, равноудаленных от точки А(2; 2) и от оси абсцисс.
16. Фокусы гиперболы находятся в точках 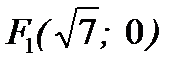 и
и  . Гипербола проходит через точку А(2; 0). Найти уравнения ее асимптот и угол между ними.
. Гипербола проходит через точку А(2; 0). Найти уравнения ее асимптот и угол между ними.
17. На эллипсе 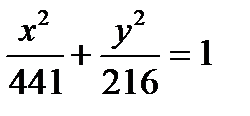 найти точки, в которых фокальные радиусы были бы взаимно перпендикулярны.
найти точки, в которых фокальные радиусы были бы взаимно перпендикулярны.
18. Найти параметр параболы 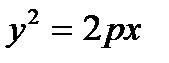 и уравнение ее директрисы, если известно, что эта парабола проходит через точки пересечения прямой
и уравнение ее директрисы, если известно, что эта парабола проходит через точки пересечения прямой  с окружностью
с окружностью 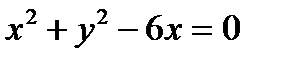 .
.
19. На гиперболе  найти точки, расстояние которых от левого фокуса вдвое меньше, чем от правого.
найти точки, расстояние которых от левого фокуса вдвое меньше, чем от правого.
20. Найти уравнение эллипса, у которого эксцентриситет равен 0,8, а фокальные радиусы одной из его точек равны 2 и 3, полагая, что большая ось эллипса совпадает с осью абсцисс, а центр – с началом координат.
21. Найти расстояние от правого фокуса эллипса  до прямой, проходящей через точку пересечения прямых
до прямой, проходящей через точку пересечения прямых  и
и 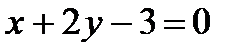 и центр окружности
и центр окружности  .
.
22. Найти общие точки эллипса  и окружности, проходящей через фокусы данного эллипса и имеющей центр в его верхней вершине.
и окружности, проходящей через фокусы данного эллипса и имеющей центр в его верхней вершине.
23. Написать уравнение гиперболы, симметричной относительно осей координат и проходящей через точки 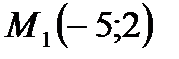 и
и 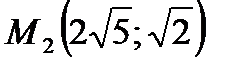 .
.
24. Написать уравнение гиперболы, зная, что она симметрична относительно координат. Уравнение асимптот гиперболы 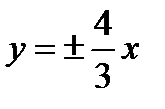 , а расстояние между фокусами
, а расстояние между фокусами  .
.
25. Написать каноническое уравнение гиперболы, зная, что расстояние одной из её вершин, лежащих на оси  , от фокусов равна 9 и 1.
, от фокусов равна 9 и 1.
26. Гипербола проходит через точку 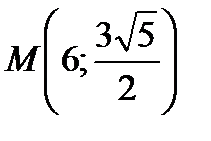 , симметрична относительно осей координат, и вещественная полуось
, симметрична относительно осей координат, и вещественная полуось  . Написать уравнение перпендикуляров, опущенных из левого фокуса гиперболы на её асимптоты.
. Написать уравнение перпендикуляров, опущенных из левого фокуса гиперболы на её асимптоты.
27. Найти расстояние от центра окружности 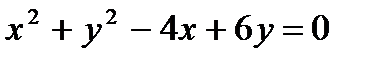 до прямой, проходящей через правый фокус гиперболы
до прямой, проходящей через правый фокус гиперболы  и точку
и точку  .
.
28. Построить гиперболу  .
.
29. Составить уравнение параболы, если она проходит через точки 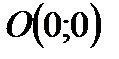 и
и  и симметрична относительно оси
и симметрична относительно оси  . Найти уравнение и длину перпендикуляра, опущенного из фокуса параболы на прямую, проходящую через правый фокус эллипса
. Найти уравнение и длину перпендикуляра, опущенного из фокуса параболы на прямую, проходящую через правый фокус эллипса  и точку
и точку 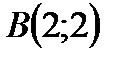 .
.
30. Построить параболу  . Найти координаты фокуса параболы. Написать уравнение прямой, проходящей через вершину параболы по углом
. Найти координаты фокуса параболы. Написать уравнение прямой, проходящей через вершину параболы по углом 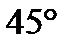 к положительному направлению оси абсцисс.
к положительному направлению оси абсцисс.
Задание № 4
Даны уравнения линии в полярной системе координат. Надо: 1) определить точки, лежащие на линии, придавая 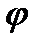 значения через промежуток, равный
значения через промежуток, равный  , начиная от
, начиная от 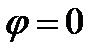 в промежутке
в промежутке 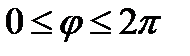 ; 2) построить линию, соединив полученные точки с помощью лекала или от руки; 3) найти уравнение этой линии в прямоугольной декартовой системе координат (положительная полуось абсцисс берется совпадающей с полярной осью, полюс – с началом прямоугольной декартовой системы координат; обе системы координат берутся правыми); 4) определить вид кривой.
; 2) построить линию, соединив полученные точки с помощью лекала или от руки; 3) найти уравнение этой линии в прямоугольной декартовой системе координат (положительная полуось абсцисс берется совпадающей с полярной осью, полюс – с началом прямоугольной декартовой системы координат; обе системы координат берутся правыми); 4) определить вид кривой.
1. 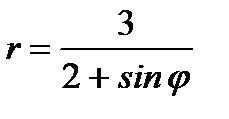
2. 
3. 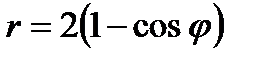
4. 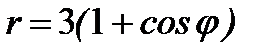
5. 
6. 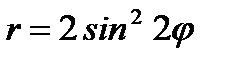
7. 
8. 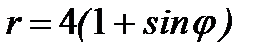
9. 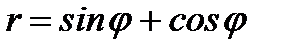
10. 
11. 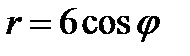
12. 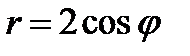
13. 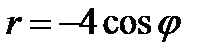
14. 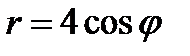
15. 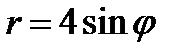
16. 
17. 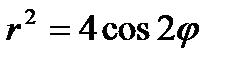
18. 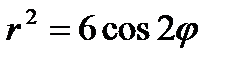
19. 
20. 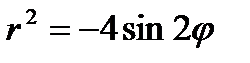
21. 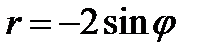
22. 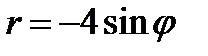
23. 
24. 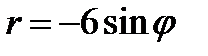
25. 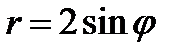
26. 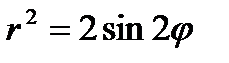
27. 
28. 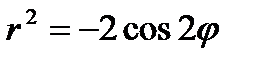
29. 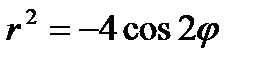
30. 
