Математическая модель кратчайшего пути

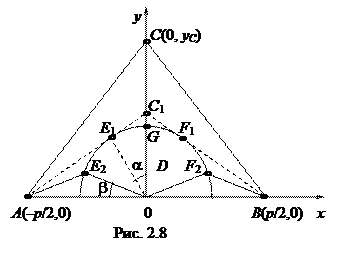В качестве примера применения нелинейных статических моделей рассмотрим задачу описания двумерного движения точки по ограниченной области (рис. 2.8). Такая задача может возникнуть при определении координат опорных точек движения инструмента на станке с ЧПУ.

Найдем кратчайший путь от точки А с координатами (х_А, у_А) до точки В с координатами (х_В, у_В) на плоскости, из которой исключена область D, определенная неравенством x² + y² £ R² .

Кратчайшим расстоянием между двумя точками на плоскости является соединяющий их отрезок прямой.

Пусть расстояние между точками А и В равно р и центр окружности, ограничивающий область D, лежит посередине между точками А и В. Тогда

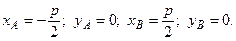
Рассмотрим путь АСВ, где точка С имеет координаты (0, у_С), а у_С – достаточно велико, чтобы отрезки АС и СВ не пересекались с областью D. Тогда по теореме Пифагора

.

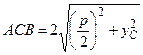Отсюда видно, что при убывании у_С путь сокращается. Будем уменьшать у_С до тех пор, пока АС не коснется окружности в точке Е₁ (С ® С₁). Этот путь является наилучшим среди путей, составленных из двух отрезков прямых линий.

Обозначим через a угол ÐЕ₁0С₁, тогда E₁C₁ + C₁F₁ = 2Rtga;

Длина дуги E₁F₁ определяется по формуле arcE₁F₁ = 2Ra .

Но tga > a для всех a Î .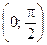

Следовательно, путь, состоящий из отрезка АЕ₁, дуги E₁F₁ и отрезка F₁B, является более коротким, чем АС₁В.

На этой стадии решения задачи мы выяснили, что кратчайший путь состоит их двух отрезков прямых линий и дуги окружности.

Для окончательного решения задачи рассмотрим путь АЕ₂ , дуга E₂F₂ , F₂B, где ÐА0Е₂ = ÐВ0F₂ = b.

Длину этого пути обозначим через S. Получим математическую модель пути:

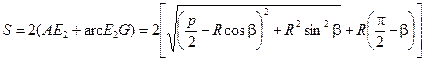. (2.16)

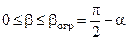, (2.16')

где a – угол между прямой Е₁0 и осью 0Y.

Ограничение (2.16') вводится потому, что при 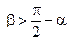прямая АЕ₁ пересечет область D, а этого не должно быть.

Задача заключается в определении угла b₀, при котором путь S будет минимальным. Необходимым условием минимума функции S(b) является равенство нулю производной:

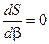. (2.17)

Рассмотрим частный случай:

P = 4; R = 1.

Тогда .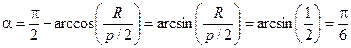

Подставив значения p и R в математическую модель (2.6), получим

.

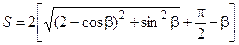Произведя некоторые преобразования, получим

.

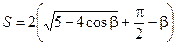Возьмем производную по b от этого выражения и приравняем ее к нулю.

.

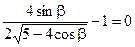Получили уравнение, решив которое относительно b, найдем значение угла b₀, при котором S минимально. Опустив промежуточные преобразования, получим cosb = 1/2.
То есть b = p/3.

Чтобы убедиться, что найденное значение является точкой минимума, необходимо исследовать вторую производную от (2.16). Если она больше нуля при b = b₀, то S(b) действительно минимальна в этой точке.

Вторая производная от S(b) имеет вид

.

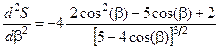Подставив в нее найденное значение b₀ = p/3, получим

.

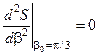Равенство нулю второй производной требует дополнительного исследования критической точки. Необходимо найти первую, не обращающуюся в нуль, производную. Если она нечетного порядка, функция не имеет в исследуемой точке ни максимума, ни минимума. Если она четного порядка и больше нуля, исследуемая точка является минимумом. Проверим третью производную от S(b) по b:

.

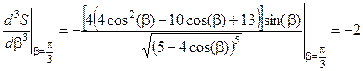Отсюда имеем, что при b = p/3 функция S(b) не имеет ни максимума, ни минимума. Действительно, из графика функции S(b) (рис. 2.9) видно, что на отрезке (2.16') функция (2.16) монотонно убывает. В точке b₀ = p/3, совпадающей с b_огр, кривая имеет точку перегиба.

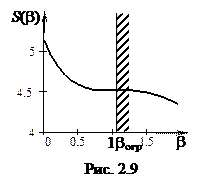
Наименьшее в области определения значение находится на границе этой области. следовательно, путь AE₁GF₁B действительно кратчайший и его длина равна S(p/3) = 4,511.

Покажем, что математическая модель (2.6) для любых p и R монотонно убывает на отрезке 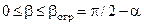и, следовательно, имеет наименьшее значение при 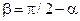. Для этого необходимо показать, что вторая производная от S(b) на интересующем нас отрезке не превышает нуля.

Вторая производная от функции (2.6) имеет вид

.

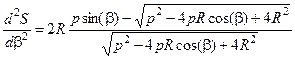Покажем, что она не превышает нуля:

.

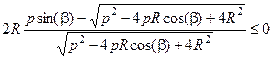Разделив обе части неравенства на 2R и умножив на корень квадратный (это можно сделать, не нарушив неравенства, так как R > 0, а корень квадратный представляет собой длину отрезка, т. е. тоже больше нуля), получим

.

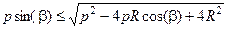Возведя обе части в квадрат (на рассматриваемом отрезке sin(b) > 0) и произведя некоторые преобразования, получим

.

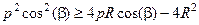В левой части неравенства cos²(b) можно заменить его минимальным значением, т.е. нулем, а в правой части – максимальным значением, т.е. единицей. Тогда получим

0 ³ 4pR – 4R² или p ³ R.

Но p действительно больше R (см. рис. 2.5).

Таким образом, аналитическую модель пути (формула (2.6)) мы использовали для доказательства того, что при b = p/2 – a путь является кратчайшим. Зная это, можно определить координаты опорных точек движения инструмента на станке с ЧПУ при любых значениях величин p и R:

А(–р/2, 0); Е₁(–Rsin(a), Rcos(a)); F₁(Rsin(a), Rcos(a)); B(p/2, 0),

где a = .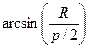

2.5. Математическая модель в виде
обыкновенных дифференциальных уравнений

Математическая модель в виде одного или нескольких обыкновенных дифференциальных уравнений (ОДУ) широко используются при изучении переходных процессов в системах автоматического регулирования (САР), при описании баллистики летательных аппаратов, а также при описании процессов движения (потоки, частицы, механические элементы).

В простейшем случае модель может иметь вид линейного дифференциального уравнения n-го порядка:

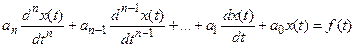
или системы дифференциальных уравнений 1-го порядка

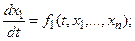
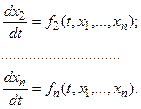
Часто встречаются смешанные задачи, а также нелинейные ОДУ.

Модель, заданная в виде дифференциальных уравнений, должна включать в себя необходимый набор начальных условий:

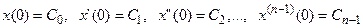
или x₁(0) = C₁, x₂(0) = C₂,…, x_n(0) = C_n .

Исследование моделей, заданных в виде обыкновенных дифференциальных уравнений, осуществляется аналитическими и численными методами. Наиболее полными являются аналитические решения, обеспечивающие всесторонний анализ полученных результатов. Но такие решения получены лишь для ограниченного числа дифференциальных уравнений. Численные методы решения позволяют найти лишь конкретные значения изучаемой функции при заданной комбинации исходных данных. Для анализа модели можно использовать некоторую совокупность решений. Однако, очевидно, что результаты анализа в этом случае могут зависеть от выбора этой совокупности.

В качестве простейшего примера математической модели механической системы может быть рассмотрена модель движения груза массой m, закрепленного на вертикальной стенке с помощью пружины жесткостью С и совершающего колебательное движение вдоль оси х в среде с вязкостью n (Рис. 2.10).

Возмущающая сила, вызывающая колебания, зависит от времени f(t). Наряду с возмущающей силой f(t) на груз действует сила инерции 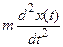, сила вязкого трения 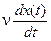, усилие пружины 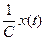. Все эти силы тормозят движение груза.

Согласно принципу Даламбера сумма всех сил, действующих на груз должна равняться нулю:

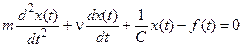. (2.18)

Начальные условия характеризуют начальное положение и начальную скорость груза:

x(0) = x₀; 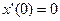. (2.19)

Уравнение (2.18) совместно с начальными условиями (2.19) представляет собой математическую модель рассматриваемой механической системы.