Числовые характеристики непрерывных CВ

Пусть непрерывная CВ Х может принимать любое значения из отрезка 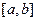. Разобьем его на частей длиной . На каждом из участков произвольно выбираем точку .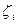

.

Тогда 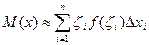- интегральная сумма

Перейдя к пределу при ,получим .

Если CВ может принимать любые значения, то рассуждая подобным образом можно получить, что

.

Аналогично, дисперсия , для непрерывной СВ дисперсия равна

.

Если вычислять 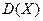по второй формуле

.

Среднее квадратичное отклонение .

Введем новые числовые характеристики

Под модой непрерывной CВ будем понимать значение CВ, при которых плотность распределения вероятностей будет достигать максимального значения.

Под медианой 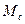будем понимать значения СВ, при котором выполняется условие:

Начальным моментом порядка k называется математическое ожидание CВ

Центральным моментом порядка k называется математическое ожидание отклонения СВ от своего математического ожидания, возведенного в k –ую степень.

Если распределение симметрично относительно математического ожидания, то все центральные моменты нечетного порядка , поэтому используется для характеристики асимметрии распределения. Для этой цели вводят коэффициент асимметрии

, .

Для описания крутизны кривой 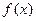вводится величина, названная эксцессом:

Для самого распространенного закона (нормального распределения) эксцесс равен нулю.

Равномерное распределение непрерывной СВ

Равномерное распределение описывается плотностью распределения

где с-константа.

Константу с найдем из условия нормировки

;

; ;

;

;

;

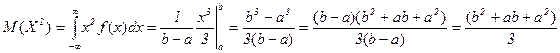Найдем F(x)

Пусть ,

,

, .

Пример 2.11. Все значения равномерно распределенной Х лежат на отрезке . Найти вероятность

Решение:

Первый способ Для , для остальных точек .

.

Второй способ Согласно геометрическому определению вероятности длина отрезка, соответствующего благоприятным исходам равна 2 и

.

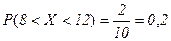Пример 2.12. Цена деления шкалы 0,2 ,показания прибора округляются до ближайшего деления. Найти вероятность того, что случайная ошибка по абсолютной величине будет меньше 0,04.

Решение:

Первый способ

0,2

0,04 0,04

( -сумма длин двух отрезков, соответствующих благоприятным исходам)

Второй способ

.

Нормальный закон распределения

Описывается плотностью распределения вероятности

Два параметра 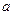и имеют следующий вероятностный смысл:

- среднеквадратическое отклонение, 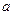- математическое ожидание.

Вероятность попадания в заданный интервал

Вводя функцию Лапласа (табулирована и нечетная) получим, что

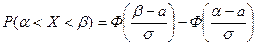
Пример 2.13.CВ X распределена по нормальному закону , . Найти вероятность того, что .

Решение:

Вероятность попадания с заданным отклонением от математического ожидания

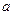
Х

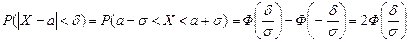
Пусть ,

Следовательно, вероятность попадания в интервал , т.е. это практически достоверное событие ; в это заключается вероятностный смысл правила .