Сравнение нейросетевого и классического подхода к задаче идентификации миграционных процессов

КЛЮЧЕВЫЕ СЛОВА:

Социодинамика, миграция, динамические системы, нейронные сети.

АННОТАЦИЯ:

Рассмотрены методы решения обратной задачи моделирования миграционных потоков. Проведён сравнительный анализ классического подхода (основанного на дискретизации и линейной регрессии) и подхода, основанного использовании нейронных сетей.

ВВЕДЕНИЕ:

Имеются две миграционные модели в виде [1]:

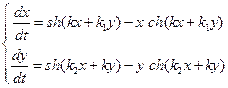(1)

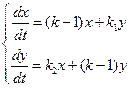(2)

Здесь (1) исходная нелинейная, а так же линеаризованная в окрестности нулевого положения равновесия - система (2). На основе этих моделей [1] можно построить прогноз миграционной динамики. Для этого необходимо определить коэффициенты моделей по имеющимся данным.

Рассмотрим три способа идентификации коэффициентов рассматриваемых моделей:

Первый способ подразумевает решение системы (2) аналитически, а затем определение коэффициентов по наилучшему соответствию решения и данных. У такого подхода есть два недостатка: невозможность его распространения на нелинейную систему (1) и необходимость решать систему заново при распространении на модели более высокого порядка.

Второй способ представляет собой дискретизацию системы (2) и определение её коэффициентов по формулам для двумерной линейной регрессии. Такой подход можно распространить на более высокие порядки, но случай нелинейной системы (1) требует построения нелинейной регрессии, что также снижает его универсальность.

Третий способ подразумевает использование нейронной сети [2,3]. Для этого можно численно решить систему для достаточно большого набора параметров, затем обучить нейронную сеть для определения каждого из них по данным, после этого вычисление необходимых коэффициентов модели по наблюдениям сведётся просто к подстановке данных в нейронную сеть. Такой подход имеет ряд преимуществ, например, большую универсальность – его применение в линейном и нелинейном случае практически не различается.

РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ:

Примем следующие обозначения: красным цветом выделен расчетный график, синим - теоретический. Рассматривался период прогноза в 5 раз больший, чем период времени, для которого строилась модель.

Рассмотрим сначала случай, когда период времени, для которого строится модель, составляет от нуля до единицы.

Приведём результаты применения второго и третьего методов для значений коэффициентов ; ; .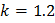

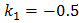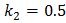1) Второй метод (линейная регрессия).

При количестве трёх входных точках – 0, 0.5 и 1, мы получили сильное расхождение расчетной модели с теоретической, однако форма графика не искажена, что легко видеть из рис.1.

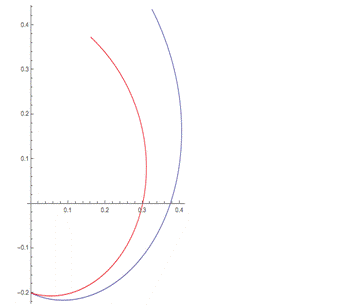
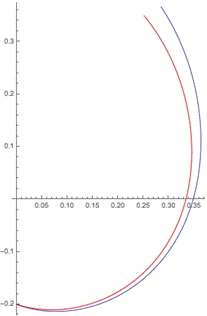
Рисунок 1 Рисунок 2

С увеличением количества точек до 10 в окрестности начала координат имеем неплохое приближение, но погрешность все еще велика (рис.2). Далее, увеличивая количество точек до 100, мы достигаем отличной точности, графики функций теоретической и расчетной модели практически совпадают. Это хорошо видно на рис.3:

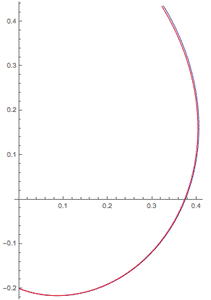
Рисунок 3

2) Метод нейросетевого моделирования. Сети обучались для набора из 300 значений параметров из области ; ;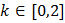

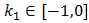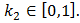
Для начала выберем количество нейронов, равное пяти. Модель полученная с использованием такой сети по трём точкам из интервала 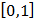(момент времени 0, 0.5 и 1) отражает основную тенденцию, однако существует значительная погрешность и искажена скорость миграционной динамики, что можно увидеть на рис.4.

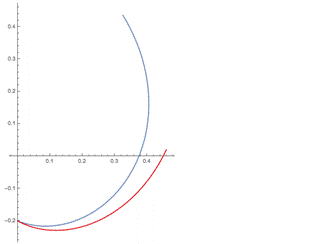
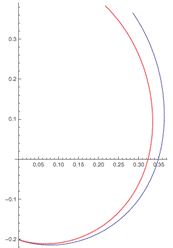
Рисунок 4 Рисунок 5

Однако, если использовать уравнения (1), то есть нелинейную модель, точность значительно лучше и искажение скорости несущественно (рис.5). Это является преимуществом нейронных сетей: нелинейная модель, которая является более точной, аппроксимируется лучше. При увеличении числа нейронов до 15 достигается хорошая точность для случая нелинейной модели, особенно в окрестности начала координат (рис.6).Также хорошо отражена основная тенденция миграции и её скорость.

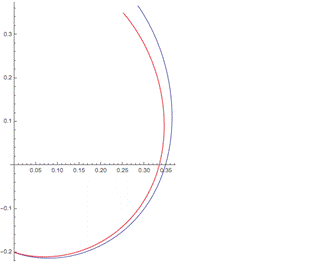
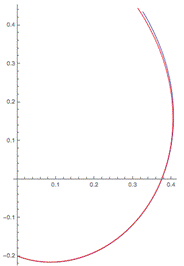
Рисунок 6 Рисунок 7

Далее, увеличив размер нейронной сети до 25-ти нейронов, при работе с линейной моделью, увидим, что она очень хорошо приближает теоретическую модель, результат сопоставим с результатом метода линейной регрессии при ста точках (рис.7).

Теперь рассмотрим интервал времени, увеличенный в 10 раз. Значения коэффициентов 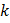, 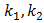остались прежними.

1) Второй метод (линейная регрессия).

Начнем рассмотрение со случая 100 точек. Исходя из рис. 8 можно сделать вывод, что погрешность становится очень большой, это говорит о том, что по 100 точкам не получается хорошо прогнозировать тенденцию миграции на достаточно большой промежуток времени (напомним, что рассматривался период прогноза в 5 раз больший, чем период времени, для которого строился прогноз) и, чтобы достичь приемлемого приближения, необходимо увеличение количества точек.

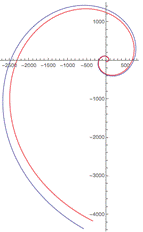
Рисунок 8 Рисунок 9

При увеличении числа точек до 1000 точность стала достаточно высока, особенно в сравнении с моделью, построенной по 100 точкам (рис.9) . Однако в подобных задачах трудно получить такое большое количество входных данных.

2) Метод нейросетевого моделирования.

Рассмотрим случай нейронной сети, состоящей из 15-ти нейронов, нелинейная модель. Если увеличить период времени в 10 раз, то точность приближения падает, но при этом расчетная модель хорошо повторяет вид графика функции теоретической модели и общая тенденция миграции сохранена (рис.10) .

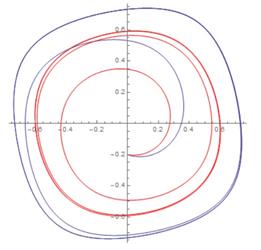
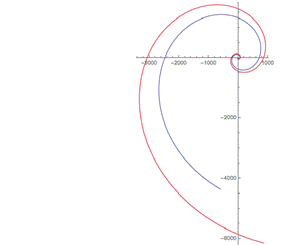
Рисунок 10 Рисунок 11

Увеличим размер нейронной сети до 25-ти нейронов. Для случая линейной модели результат будет в несколько раз лучше линейной регрессии, построенной по ста точкам, но хуже, чем по тысяче точек, погрешность достаточно велика, однако это не так важно, поскольку линейная модель сама по себе имеет некоторую неточность (рис. 11). При работе с нелинейной моделью, мы достигаем даже при увеличении периода времени в 10 раз, мы получаем отличное приближение, причем на всех участках, что видно на рисунке 12.

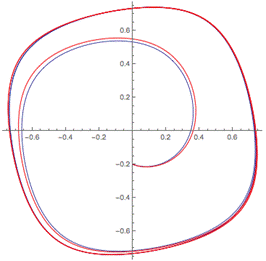
Рисунок 12

ВЫВОДЫ:

Исходя из приведенных данных , можно сделать несколько выводов:

1. Нейронные сети при достаточном количестве нейронов (в данной задаче - больше или равном 25) позволяют хорошо восстановить модель. Для того чтобы достичь той же точности с использованием линейной регрессии, необходимо большое количество входных данных. Кроме того, такой метод вызывает существенные затруднения для случая нелинейной модели, которая является более точной;

2. Нейронные сети могут работать как и линейной моделью, так и с нелинейной, точность аппроксимации существенно зависит от количества нейронов, и не сильно - от количества входных данных, это дает нейронным сетям большое преимущество над методом линейной регрессии .У нейронных сетей имеется ряд заметных преимуществ по сравнению с другими методами приближения и прогнозирования: универсальность, точность, способность к обучению. Нейронные сети уже являются универсальным методом решения многих сложных прикладных задач, полученные результаты лишь подтвердили это.

Проведённые вычислительные эксперименты показывают, что применение нейронных сетей для решения обратной задачи моделирования миграционных потоков является оптимальным способом.

Литература.

1. Вайдлих В. Социодинамика: системный подход к математическому моделированию в социальных науках. М.: Едиториал УРСС, 2005. 480с.

2. Васильев А.Н., Тархов Д.А .– Нейросетевое моделирование. Принципы. Алгоритмы. Приложения. – СПб.:Изд-во Политехн. Ун-та. 2009. - 528 с.

3. Тархов Д.А. Нейросетевые модели и алгоритмы. – М.: Радиотехника, 2014. – 352 с.