Тема 2. Обратная матрица. Ранг матрицы

Раздел 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

Тема 1. Матрицы и определители

Матрицы, основные понятия и определения

Операции над матрицами

Линейные операции над матрицами

Пример 1. Даны матрицы 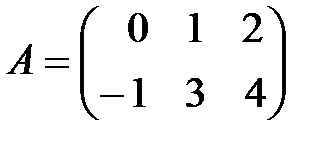, 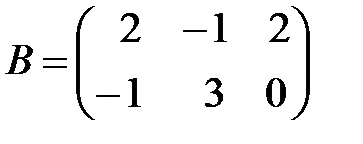. Найти 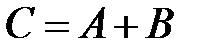и .

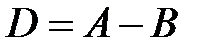Решение: 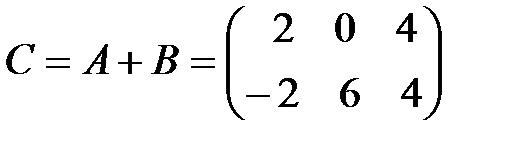, а .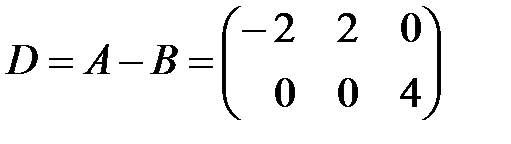

Пример 2. Дана матрица 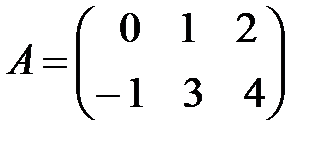. Найти .

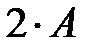Решение:При умножении матрицы на число 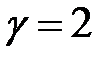все ее элементы умножаются на это число, следовательно, будем иметь: .

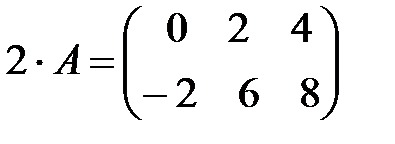Произведение матриц

Можно умножать лишь матрицы, у которых число столбцов в матрице, стоящей в произведении слева равно числу строк в матрице, стоящей в произведении справа.

Пример 3. Даны матрицы 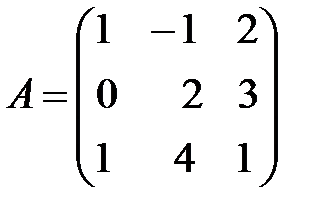и 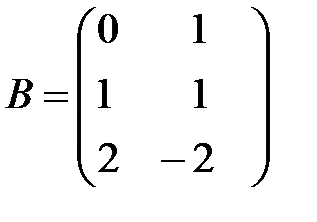. Найти 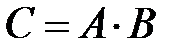. Решение:Число столбцов в матрице 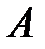равно числу строк в матрице 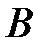. Чтобы получить элемент 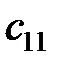нужно найти сумму произведений элементов первой строки матрицы 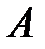на соответствующие элементы первого столбца матрицы 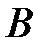. Для вычисления значения элемента 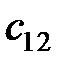нужно сложить произведения элементов первой строки матрицы 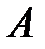на соответствующие элементы второго столбца матрицы и т.д., т.е. будем иметь:

.

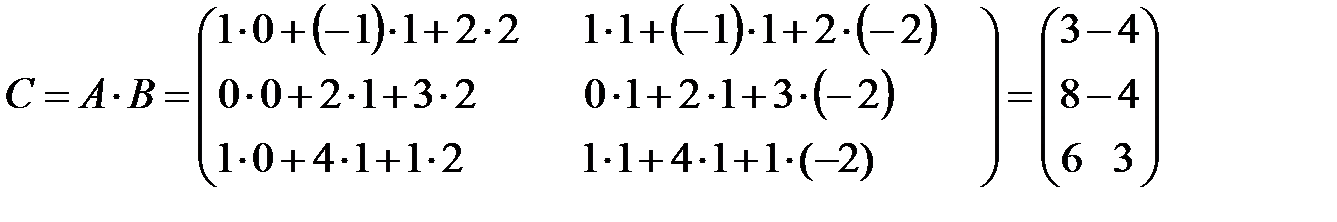Пример 4. Дана матрица .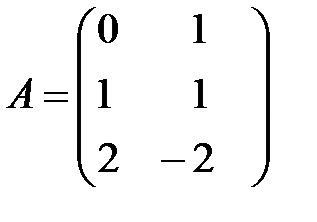

Записать транспонированную матрицу .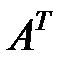

Решение:При транспонировании заменяем строки столбцами с теми же номерами, т.е. для матрицы 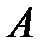транспонированной 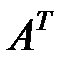будет матрица вида: .

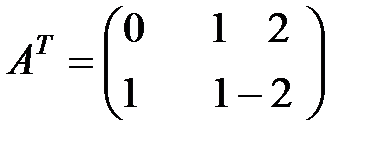Определители

Пример 5. Для матрицы 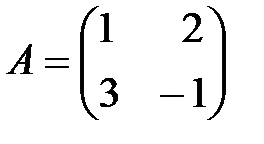найти определитель.

Решение: .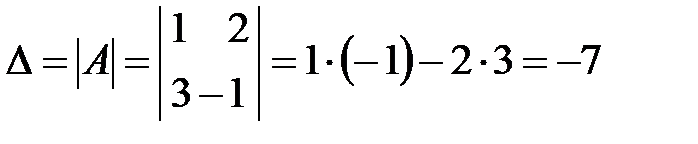

Пример 6. Вычислить определитель третьего порядка .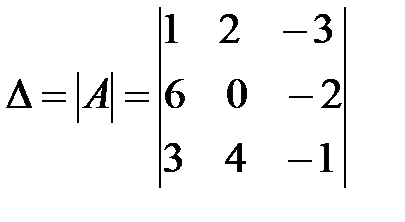

Решение: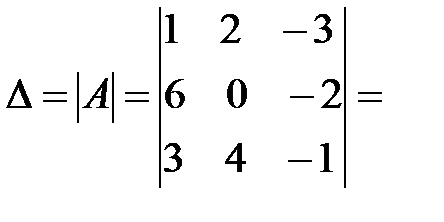

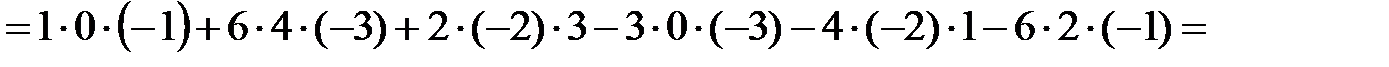
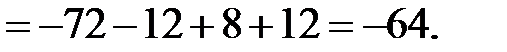
Свойства определителей:

1⁰. При транспонировании матрицы ее определитель не изменяется.

2⁰. При перестановке соседних строк (столбцов) определитель меняет знак на противоположный.

3⁰. Определитель равен нулю, если все элементы строки (столбца) определителя равны нулю.

4⁰. Определитель равен нулю, если имеются несколько строк (столбцов) с пропорциональными (в частности равными) элементами.

5⁰. Общий множитель всех элементов строки (столбца) можно вынести за знак определителя.

6⁰. Значение определителя не изменится, если к элементам его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число .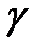

Замечание. Для определителей третьего и более высоких порядков справедливы еще два свойства, которые дают другие способы вычисления определителей.

Для дальнейшего изложения необходимо ввести понятия алгебраических дополнений 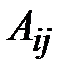и миноров 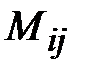для элемента .

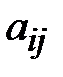Определение.Минором 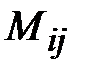для элемента 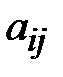определителя 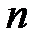-го порядка называется определитель 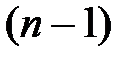-го порядка, полученный из исходного вычеркиванием 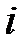-ой строки и -го столбца.

Определение. Алгебраическим дополнением 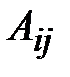элемента 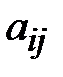называется минор 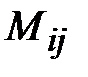, взятый с определенным знаком, а именно: .

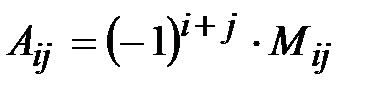7⁰. (Теорема о разложении). Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

Определитель можно разложить по элементам любой строки (столбца). Например, разложение определителя третьего порядка по 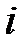-ой строке дает формула:

,

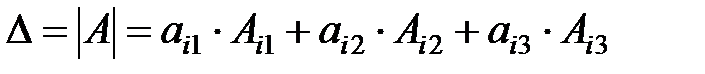где 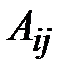- алгебраические дополнения соответствующих элементов .

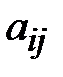8⁰. Если определитель имеет треугольный или диагональный вид (определитель, записанный для треугольной или диагональной матрицы), то он равен произведению элементов его главной диагонали. Например:

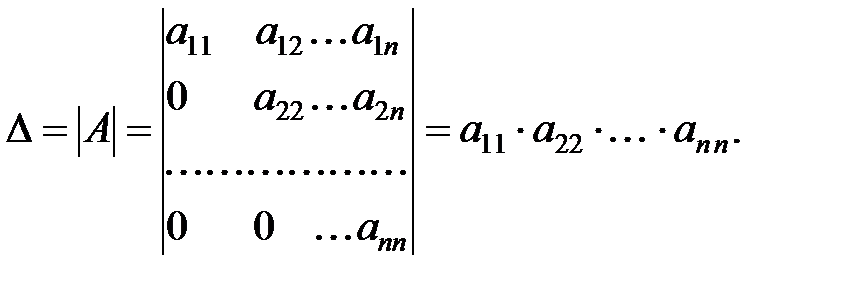
Указание. Для приведения определителя к треугольному виду следует воспользоваться свойством 6⁰.

Пример 7.Для определителя из примера 6 найт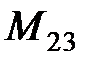и и .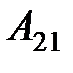

Решение:Чтобы найти 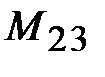вычеркнем мысленно в данном определителе вторую строку и третий столбец, получим определитель второго порядка:

.

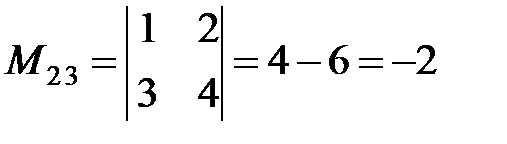Для нахождения 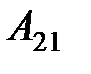необходимо 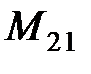умножить на 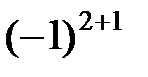, т.е. 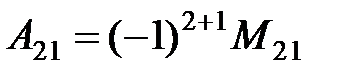, следовательно .

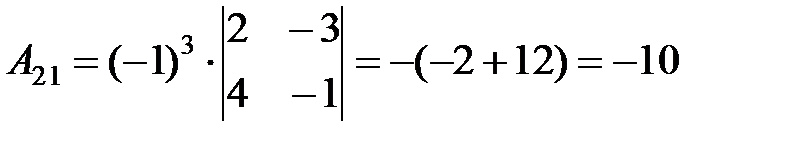Пример 8. Вычислить определитель из примера 6 разложением по второй строке:

Решение: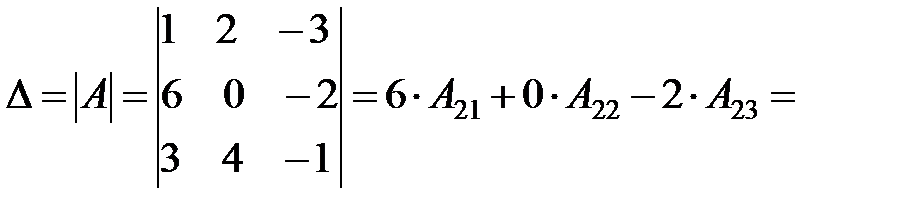

.

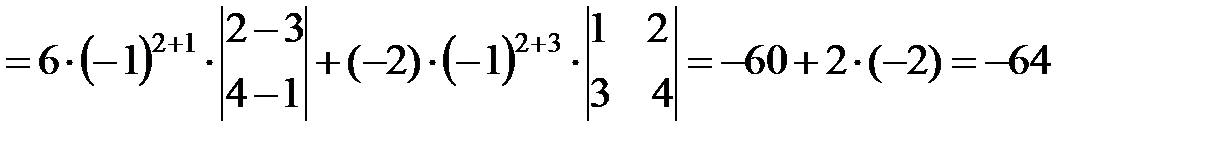Определители для удобства вычислений можно приводить к треугольному виду, применяя свойства.

Пример 9.Вычислить определитель из примера 6, приведя его к треугольному виду.

Решение:

.

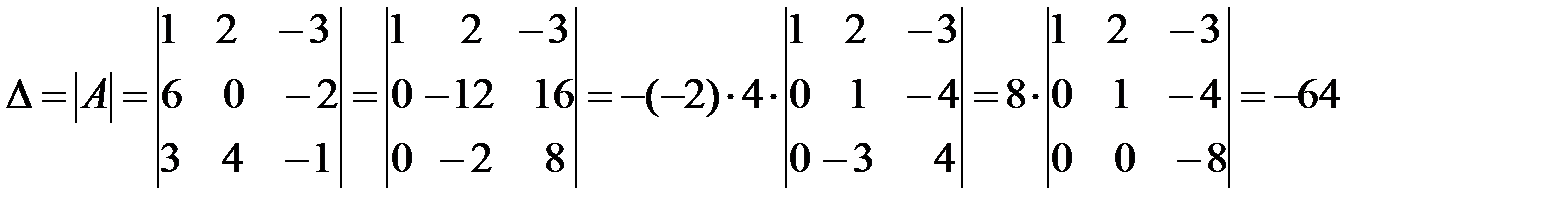Здесь в первом определителе элементы первой строки умножили на –6 и прибавили к соответствующим элементам второй; элементы первой же строки умножили на –3 и прибавили к соответствующим элементам третьей строки (свойство 6). Получили второй определитель, в котором элементы второй и третьей строк имеют общий множитель, которые вынесены за знак третьего определителя (свойство 5): из второй строки вынесен множитель 4, а из третьей –2, также вторую и третью строки поменяли местами и поменяли перед определителем знак (свойство 2). В третьем определителе элементы второй строки умножили на 3 и прибавили к соответствующим элементам третьей. Получили определитель треугольного вида (все элементы под главной диагональю равны нулю), который равен произведению элементов на главной диагонали (свойство 8).

Тема 2. Обратная матрица. Ранг матрицы.

Элементарные преобразования матриц

Пример 10.Для матрицы 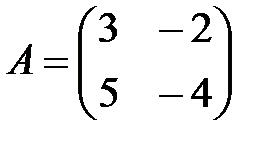найти обратную матрицу 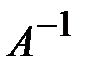. Сделать проверку.

Решение:применим описанный выше алгоритм нахождения .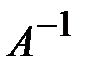

1. Вычисляем определитель: 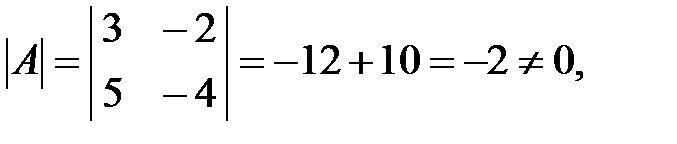следовательно, матрица неособенная или невырожденная.

2. Запишем транспонированную матрицу 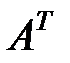для матрицы :

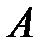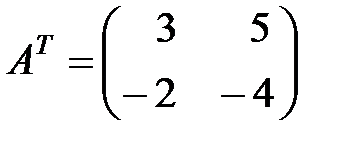
3. Вычислим присоединенную матрицу 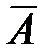. Для этого найдем алгебраические дополнения для всех элементов транспонированной матрицы:

.

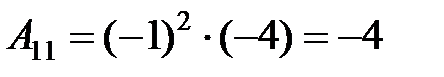
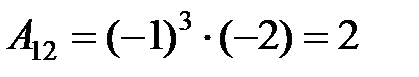
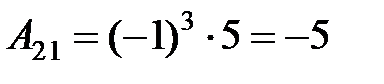
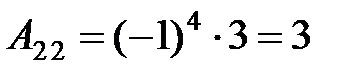Запишем присоединенную матрицу .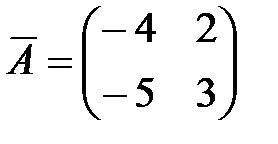

4. Вычислим обратную матрицу по формуле (1.5): .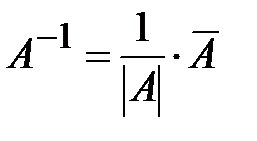

.

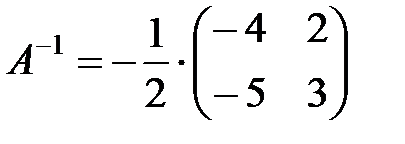Проверка. Воспользуемся определением (1.4) обратной матрицы:

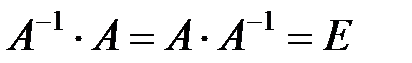. Найдем произведение

= =

= .

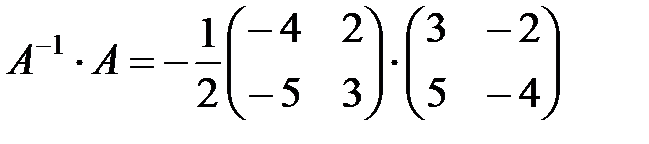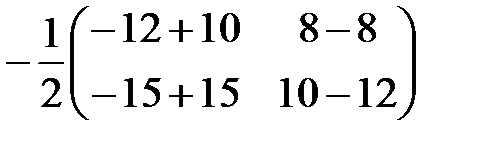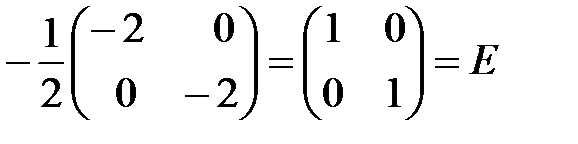Пример 11.Для матрицы 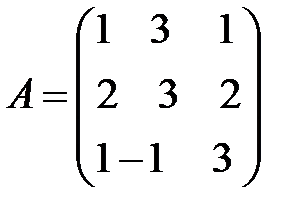найти обратную матрицу 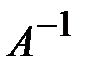. Сделать проверку.

Решение:

1. Вычисляем определитель 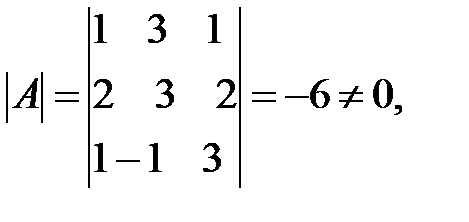следовательно, матрица 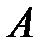неособенная или невырожденная.

2. Запишем транспонированную матрицу 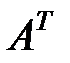для матрицы : .

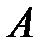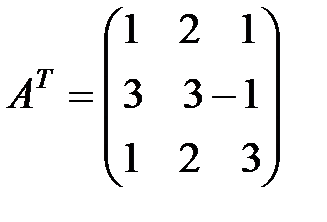3. Вычислим присоединенную матрицу 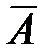; для этого найдем алгебраические дополнения для всех элементов транспонированной матрицы.

.

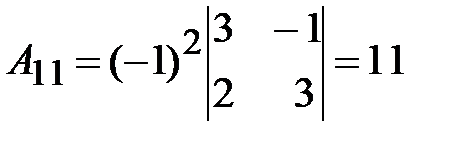
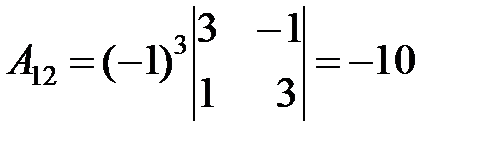
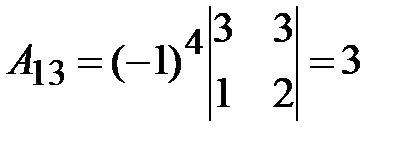
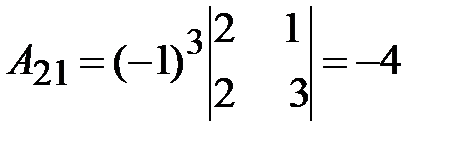
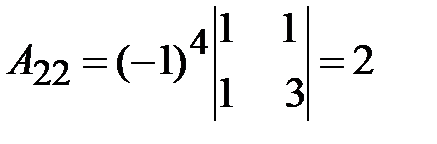
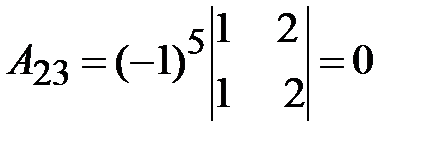
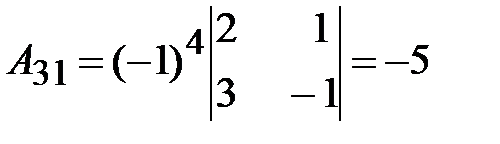
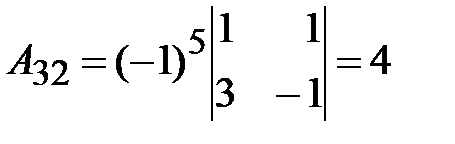
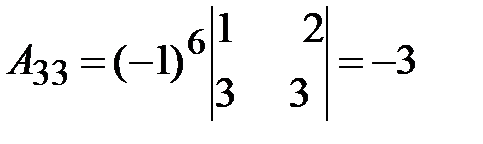Итак, присоединенная матрица имеет вид: .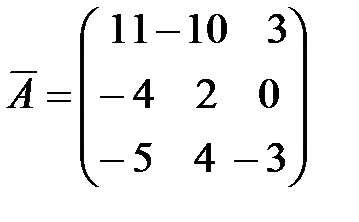

4. Запишем обратную матрицу, используя формулу (1.5): .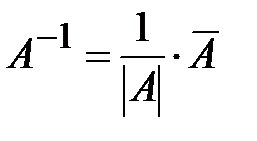

.

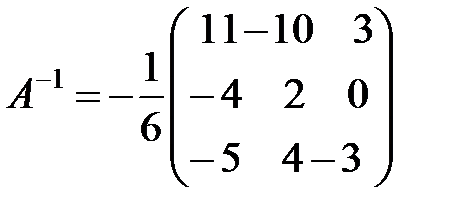Проверка. Воспользуемся определением (1.4) обратной матрицы:

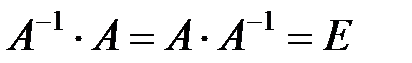. Найдем произведение

.

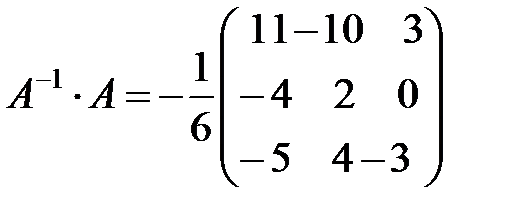
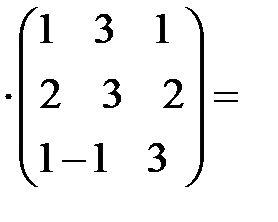
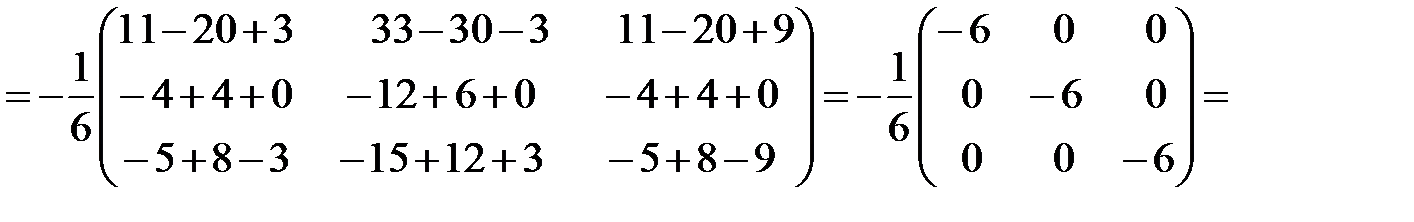
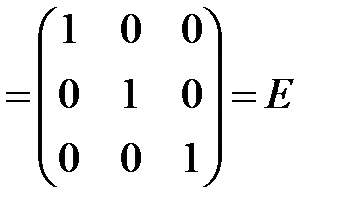Для нахождения ранга следует с помощью элементарных преобразований привести матрицу к треугольному виду. Преобразованная матрица будет эквивалентна исходной, т.е. иметь тот же ранг, но, учитывая свойство определителей 8⁰, в матрице треугольного вида легко определяется наивысший порядок минора не равного нулю.

К элементарным преобразованиям относятся:

1) перемена местами строк;

2) умножение строки на произвольное, отличное от нуля число;

3) прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на некоторое число.

Пример 12. Найти ранг матрицы: .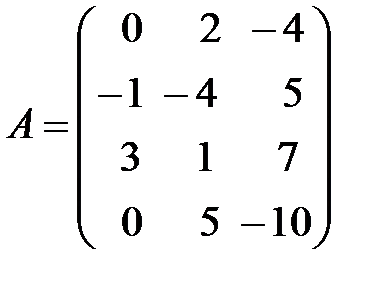

Решение:Преобразуем матрицу к треугольному виду с помощью элементарных преобразований.

~ ~ ~ ~ .

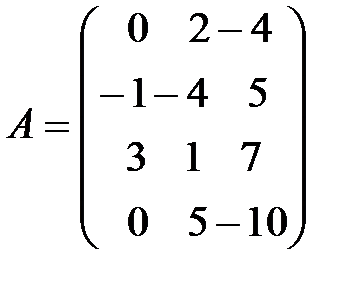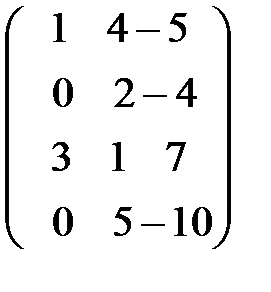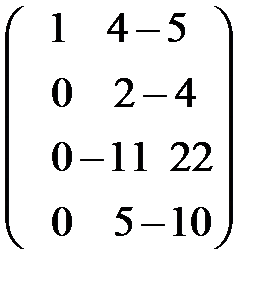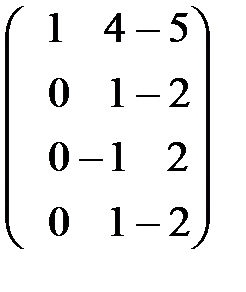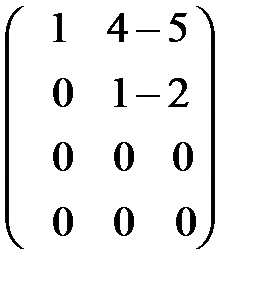Вторая эквивалентная матрица получается, если первую строку умножить на (–1) и поменять местами со второй строкой (элементарные преобразования 1, 2). Итак, на месте элемента 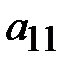получили единицу. Теперь все элементы первого столбца должны быть равными нулю. Следовательно, на месте элемента 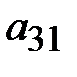должен быть ноль. Умножим элементы первой строки на (–3) и прибавим к соответствующим элементам третьей строки (элементарное преобразование 3). Получили третью матрицу, в которой вторую строку разделим на 2, третью на 11, четвертую на 5. Так получена четвертая матрица, в которой на месте элемента 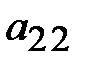стоит единица. Теперь необходимо во втором столбце под элементом 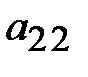получить нулевые элементы. Если к элементам третьей строки прибавить соответствующие элементы второй и к элементам четвертой строки прибавить элементы второй, умноженные на (–1), то получим пятую матрицу диагонального вида, причем на главной диагонали количество ненулевых элементов равно двум. Определитель второго порядка, расположенный в левом верхнем углу отличен от нуля (он равен 1), следовательно, ранг R=2.