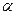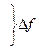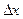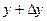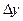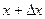Первый замечательный предел
Первым замечательным пределом называется:
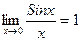
Доказательство: возьмем круг радиуса 1. Обозначим радианную меру угла MOB через x (рис.3) Пусть 0<x<π/2;

| |
|
|
|




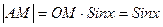 , а дуга MB численно равна центральному углу x, BC=tgx. Очевидно, что S∆MOB<SсекторМОВ<S∆COB на основании геометрических формул это равенство можно записать в виде:
, а дуга MB численно равна центральному углу x, BC=tgx. Очевидно, что S∆MOB<SсекторМОВ<S∆COB на основании геометрических формул это равенство можно записать в виде: 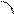

|
|
|
|
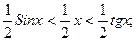 разделим неравенство на ½ Sinx>0. получим:
разделим неравенство на ½ Sinx>0. получим: 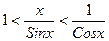 или
или 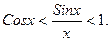 Переходя к пределу при x→0 получим:
Переходя к пределу при x→0 получим: 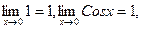 тогда по теореме о пределе промежуточной функции получим:
тогда по теореме о пределе промежуточной функции получим: Рис.3 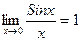 при x>0
при x>0
при x<0, 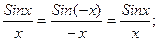 т.е.
т.е.
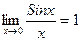 при любых x.
при любых x.
Пример. Найти 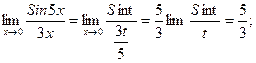
8) Второй замечательный предел.
Как мы показали, предел числовой последовательности
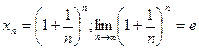
Докажем, что к числу е стремится и функция 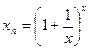 при x→∞,т.е.
при x→∞,т.е. 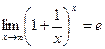
1. пусть x→+∞. Каждое значение x заключено между двумя целыми положительными числами 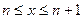 , где
, где 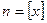 -целая часть x. Отсюда следует
-целая часть x. Отсюда следует 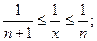
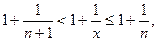 поэтому
поэтому 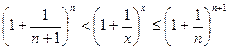 если
если 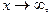 то и
то и 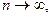 поэтому
поэтому 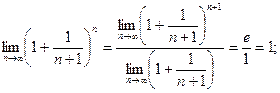
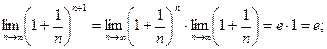
По теореме о пределе промежуточной функции получим:
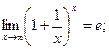
2) Пусть 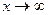 . Сделаем подстановку –x=t, тогда
. Сделаем подстановку –x=t, тогда
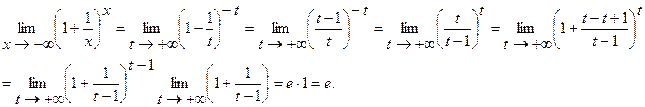
Таким образом 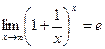 , если в этом уравнении положить
, если в этом уравнении положить 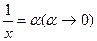
получим 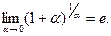
Этот предел широко используется для вычисления других пределов.
Пример: Найти 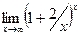 . Обозначив x=2t, имеем
. Обозначив x=2t, имеем 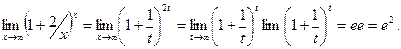
8) Сравнение бесконечно малых функций.
Отношение двух б.м.ф. может вести себя разным образом: быть конечным числом, бесконечно большой функцией , бесконечно малой или вообще не стремится ни к какому пределу.
Две б.м.ф. сравнивают с помощью их отношения. Пусть 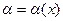 и
и 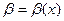 -есть б.м.ф. при x→x0, т.е.
-есть б.м.ф. при x→x0, т.е. 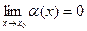 и
и 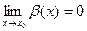 . Тогда возможны четыре случая:
. Тогда возможны четыре случая:
1. если 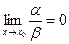 , то α- бесконечно малая более высокого порядка чем β;
, то α- бесконечно малая более высокого порядка чем β;
2. если 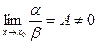 , то α и β- бесконечно малые одного порядка;
, то α и β- бесконечно малые одного порядка;
3. если 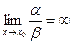 , то α- бесконечно малая более низкого порядка чем β;
, то α- бесконечно малая более низкого порядка чем β;
4. если 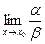 - не существует, то α и β называют несравнимыми бесконечно малыми.
- не существует, то α и β называют несравнимыми бесконечно малыми.
9) Непрерывность функций.
Понятие непрерывности функции является фундаментальным в матанализе.
1. Функция f(x) называется непрерывной в точке x0, если предел этой функции, и ее значение в этой точке равны, т.е. 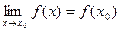 . (1)
. (1)
Определение непрерывности можно дать и с позиций теоремы о пределах;
2. Функция f(x) называется непрерывной в точке х0, если для любого 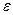 >0 существует такое
>0 существует такое 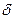 >0, что при всех x удовлетворяющих неравенству |x-x0|<
>0, что при всех x удовлетворяющих неравенству |x-x0|< 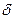 , выполняется неравенство |f(x)-f(x0)|<
, выполняется неравенство |f(x)-f(x0)|< 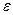 ;
;
3. Для практического использования полезно сформулировать еще одно определение непрерывности функции. Назовем разность ∆x=x-x0- приращением аргумента в точке x0 , а разность ∆y=f(x)-f(x0)- приращением функции в точке x0, обусловленное приращением аргумента ∆x. Таким образом, ∆x=x-x0,∆y=f(x)-f(x0), поскольку условия x →x0 и x-x0 →0 равносильны, то равенство (1) можно записать 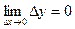 - еще одно определение непрерывности функции.
- еще одно определение непрерывности функции.
10) Непрерывность функции в интервале и на отрезке.
Функция y=f(x)называется непрерывной в интервале (a,b), если она непрерывна в каждой точке этого интервала. Функция y=f(x) называется непрерывной на отрезке [a,b], если она непрерывна в интервале (  ,b), в точке x=
,b), в точке x=  непрерывна справа(т.е.
непрерывна справа(т.е. 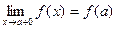 ), а в точке x=b непрерывна слева (т.е.
), а в точке x=b непрерывна слева (т.е. 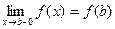 ).
).
11) Точки разрыва и их классификация
Точка x0 называется точкой разрыва функции f(x) , если эта функция в данной точке не является непрерывной.
Различают точки разрыва:
- Первого рода ( когда существуют односторонние конечные пределы функций слева и справа при x→ x0, не равные друг другу);
- Второго рода (когда хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует)
|

|
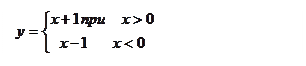
|
|
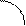
|
|
|

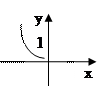
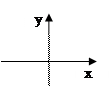
 Так точка x1=0 на рис.
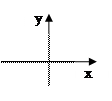
Так точка x1=0 на рис.  - точка разрыва первого порядка, а на рис.б)- точка разрыва второго порядка. К точкам разрыва первого порядка относятся также точки устранимого разрыва, когда предел функции при x→x0 существует, но не равен значению функции в этой точке.
- точка разрыва первого порядка, а на рис.б)- точка разрыва второго порядка. К точкам разрыва первого порядка относятся также точки устранимого разрыва, когда предел функции при x→x0 существует, но не равен значению функции в этой точке.
|
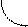
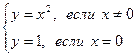 (рис.в). Точка x=0 этой функции является точкой устранимого разрыва. Положив y(x)=0 вместо y(x)=1, при x=0, разрыв устранится. Функция станет непрерывной.
(рис.в). Точка x=0 этой функции является точкой устранимого разрыва. Положив y(x)=0 вместо y(x)=1, при x=0, разрыв устранится. Функция станет непрерывной. 12) Свойства функций.
а) для функций, непрерывных в точке:
Теорема о непрерывности функций вытекают непосредственно из соответствующих теорем о пределах.
Теорема 1. Сумма, произведение и частное двух непрерывных функций в точке x0 есть функция непрерывная( за исключением тех значений аргумента, в которых делитель равен нулю). Доказательство следует из теоремы о непрерывности и аналогичных свойств пределов функций.
Теорема 2. Пусть функция y=f(u) непрерывна в точке u0, а функция u= 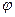 (x) непрерывна в точке u0=φ(x0). Тогда сложная функция y=f[φ(x)] непрерывна в точке x0.
(x) непрерывна в точке u0=φ(x0). Тогда сложная функция y=f[φ(x)] непрерывна в точке x0.
Доказательство: в силу непрерывности функции u= 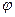 (x),
(x), 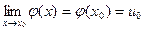 , т.е. при
, т.е. при
x→ x0 имеем u→ u0. Поэтому вследствие непрерывности y=f(u) имеем:
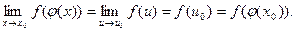
Это доказывает, что функция y=f(φ(x)) непрерывна в x0.
Теорема 3. Если y=f(x) непрерывна в точке x0 и f(x0)>0, то существует такая окрестность точки x0, в которой f(x)>0.Доказательство основано на том, что малому приращению аргумента ∆x →0, соответствует какое угодно малое приращение ∆y в силу определения непрерывности. Так что знак функции y=f(x) в окрестностях (x0-∆x,x0+∆x) не изменится. Вообще следует отметить, что функция y=f(x) будет непрерывной на промежутке x, если она непрерывна в каждой точке этого промежутка. Можно доказать, что все элементарные функции непрерывны в области из значения.
б) для функций, непрерывных на отрезке:
 Теорема1. Если функция y=f(x) непрерывна на отрезке [a,b], то она ограничена на этом отрезке.
Теорема1. Если функция y=f(x) непрерывна на отрезке [a,b], то она ограничена на этом отрезке.
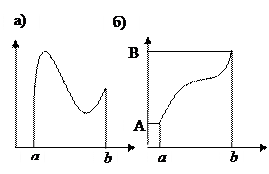
Теорема 2. Если функция y=f(x) непрерывна на отрезке [a,b], то она достигает на этом отрезке своего наименьшего и наибольшего значения (теорема Вейерштрасса) (рис. a).
Теорема 3. Если функция y=f(x) непрерывна на отрезке [a,b] и принимает на его концах неравные значения f(a)=A и f(b)=B, то на этом отрезке она принимает все промежуточные значения между A и B.(рис.б)
|
7. Производная.
Понятие производной относится к одному из основных понятий в математике. Она широко используется при решении задач, связанных с изменением различных функций во времени.
Пусть нам задана произвольная функция 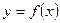 на некотором интервале
на некотором интервале 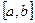 . Придадим аргументу
. Придадим аргументу 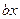 приращение
приращение 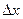 . Тогда соответствующее приращение функции составит
. Тогда соответствующее приращение функции составит 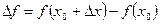 . Располагая этими значениями мы можем ввести понятие производной функции в точке
. Располагая этими значениями мы можем ввести понятие производной функции в точке 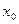 следующим образом. Производной функции f(x) в точке
следующим образом. Производной функции f(x) в точке 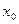 называется предел отношения приращения функции в этой точке к приращению аргумента при
называется предел отношения приращения функции в этой точке к приращению аргумента при 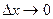 . Итак, по определению производная
. Итак, по определению производная 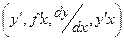 равна
равна 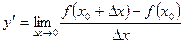 или
или 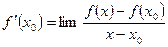
Функция 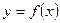 , имеющая производную в каждой точке интервала (a,b) называется дифференцируемой на этом интервале, а сама операция нахождения производной – дифференцированием.
, имеющая производную в каждой точке интервала (a,b) называется дифференцируемой на этом интервале, а сама операция нахождения производной – дифференцированием.
Если функция имеет производную в каждой точке множества Х, то и производная тоже является функцией от аргумента 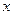 , определенной на Х.
, определенной на Х.
1) механический и геометрический смысл производной.
а) механический смысл.
Пусть 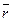 (t) – вектор характеризующий положение точки в различные моменты времени t. Если мы зададим два момента времени t1 и t2, то вектор
(t) – вектор характеризующий положение точки в различные моменты времени t. Если мы зададим два момента времени t1 и t2, то вектор 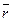 изменится за промежуток
изменится за промежуток 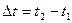 на величину
на величину 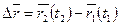
 , и мы можем ввести понятие средней скорости перемещения
, и мы можем ввести понятие средней скорости перемещения 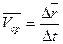 .
.
Если мы возьмем предел от этого соотношения при условии 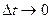 , то получим
, то получим
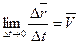 , где V будет определять значение мгновенной скорости в момент времени
, где V будет определять значение мгновенной скорости в момент времени 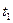 . Понятие производной можно использовать при описании любого процесса зависящего от времени и везде производная будет определять скорость того или иного процесса в какой-то конкретный момент времени, в этом и состоит физический смысл производной.
. Понятие производной можно использовать при описании любого процесса зависящего от времени и везде производная будет определять скорость того или иного процесса в какой-то конкретный момент времени, в этом и состоит физический смысл производной.
б) Геометрическая интерпретация.
 |
|
|
|
|
|
|

|
|
|





|
|
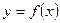 изображенная на рисунке. По определению производной:
изображенная на рисунке. По определению производной: 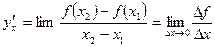 , но
, но 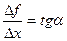 , тогда и
, тогда и 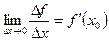 будет равен значению углового коэффициента касательной проведенной к точке М
будет равен значению углового коэффициента касательной проведенной к точке М 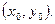 ,в этом и заключается геометрический смысл производной.
,в этом и заключается геометрический смысл производной. 2) связь между непрерывностью и дифференцируемостью функции.
Теорема. Если функции дифференцируема в некоторой точке, то она и непрерывна в ней. Обратное утверждение вообще говоря не верно, т.е. если функция непрерывна, то она необязательно дифференцируема. Пример 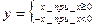 в точке
в точке 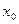 эта функция непрерывна, но не дифференцируема. Докажем теорему. Пусть дана функция
эта функция непрерывна, но не дифференцируема. Докажем теорему. Пусть дана функция 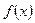 дифференцируемая в точке х0, следовательно должен существовать предел
дифференцируемая в точке х0, следовательно должен существовать предел 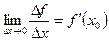 , но в соответствии с теоремой о связи функции, ее пределах и бесконечно малой функции
, но в соответствии с теоремой о связи функции, ее пределах и бесконечно малой функции 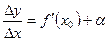 , где
, где 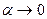 при
при 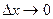 отсюда
отсюда 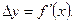
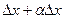 переходя к пределу при
переходя к пределу при 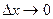 получим
получим 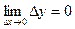 , что означает, что
, что означает, что 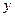 – непрерывно в точке
– непрерывно в точке 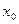 . Обратная теорема неверна: Примером такой функции является
. Обратная теорема неверна: Примером такой функции является 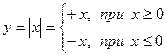 , эта функция непрерывна в точке
, эта функция непрерывна в точке 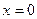 , но не дифференцируема в ней. Действительно при
, но не дифференцируема в ней. Действительно при 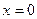 имеем:
имеем:
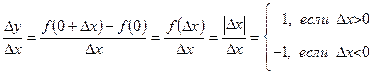
Отсюда следует, что 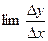 не существует, т.е.
не существует, т.е. 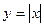 не имеет производной в точке
не имеет производной в точке 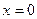 , и график функции не имеет касательной в точке О (0;0). В этом случае говорят, что функция имеет односторонние производные (справа и слева). Их обозначают, как
, и график функции не имеет касательной в точке О (0;0). В этом случае говорят, что функция имеет односторонние производные (справа и слева). Их обозначают, как 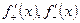 . Не существует производных и в точках разрыва функции.
. Не существует производных и в точках разрыва функции.
Если функция 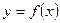 имеет непрерывную производную
имеет непрерывную производную 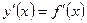 в некотором интервале
в некотором интервале 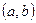 , то функцию называют гладкой.
, то функцию называют гладкой.
3) Производная суммы, разности и произведения и частного функции.
Нахождение производных функций, исходя из ее определения, иногда связано со значительными трудностями. Поэтому для упрощения процесса дифференцирования на практике используют ряд правил задаваемых с помощью нескольких теорем.
Пусть нам задано две дифференцируемые на 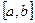 функции
функции 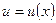
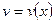 тогда:
тогда:
Теорема 1 Производная суммы (разности) двух функций равна сумме (разности) производных, т.е. 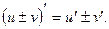
Доказательство. Пусть 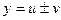 тогда,
тогда, 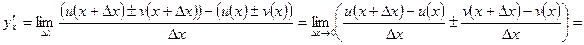
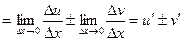 или
или 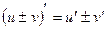 .
.
В общем случае теорема справедлива для любого конечного числа слагаемых.
Теорема 2 Производная произведения двух функций равно произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго т.е. 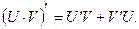
Пусть 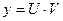 , тогда
, тогда 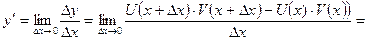
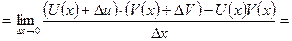
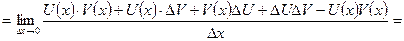
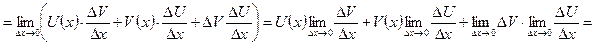
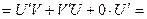
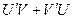
Следствия: 1. можно показать, что 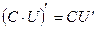 где С -
где С - 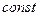
2. 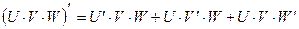
Теорема 3 Производная частного двух функций 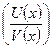 , если
, если 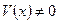 равно дроби, числитель которой равен разности произведения знаменателя дроби на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя, т.е.
равно дроби, числитель которой равен разности произведения знаменателя дроби на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя, т.е. 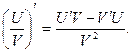
Доказательство. Пусть 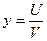 , тогда
, тогда 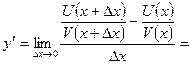
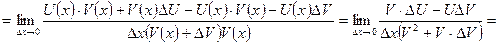
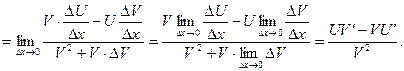
Следствия: 1) 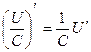 2)
2) 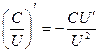 где С – const.
где С – const.
4)Производная сложной и обратной функции.
Пусть 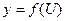 и
и 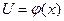 , тогда
, тогда 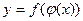 – сложная функция с промежуточным аргументом и независимым аргументом х. Для определения производной подобной функции удобно пользоваться следующей теоремой.
– сложная функция с промежуточным аргументом и независимым аргументом х. Для определения производной подобной функции удобно пользоваться следующей теоремой.
Теорема. Если функция 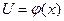 имеет производную
имеет производную 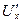 в точке х, а функция
в точке х, а функция 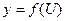 имеет производную
имеет производную 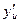 в соответствующей точке
в соответствующей точке 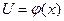 , то сложная функция
, то сложная функция 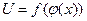 , имеет производную
, имеет производную 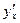 в точке х, которая находится по формуле
в точке х, которая находится по формуле 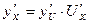 ;
;
Доказательство. Пусть 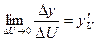 . Отсюда, по теореме о связи функции, ее пределе и б.м.ф. имеем
. Отсюда, по теореме о связи функции, ее пределе и б.м.ф. имеем 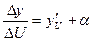 или
или 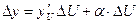 (1), где
(1), где 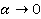 . При
. При 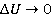 , функция
, функция 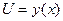 имеет производную в точке х:
имеет производную в точке х: 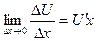 , поэтому
, поэтому 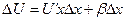 , где
, где 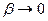 при
при 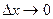 .
.
Подставив значение 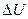 в (1) получим
в (1) получим
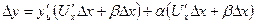 или
или
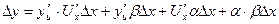 разделив на
разделив на 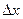 и перейдя к пределу при
и перейдя к пределу при 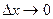 получим
получим 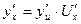
Это правило остается в силе, если промежуточных аргументов несколько. Так если 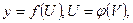 а
а 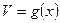 то
то 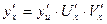 , если
, если 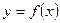 , а
, а 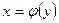 , то можно показать, что
, то можно показать, что 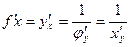 .
.
5) Производная основных элементарных функций.
1. степенная функция 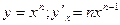
Схема доказательства 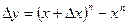 – раскладывается по формуле бинома Ньютона и т.д. и получаем все что надо.
– раскладывается по формуле бинома Ньютона и т.д. и получаем все что надо.
2. Показательная функция 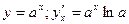 . Докажем сначала для
. Докажем сначала для 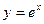
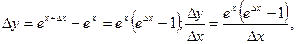 берем предел при
берем предел при 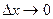
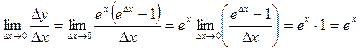 .(Использовали
.(Использовали 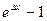 =∆x, при x→0)
=∆x, при x→0)
Т.е. 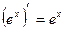
Теперь пусть 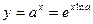 и дифференцируя
и дифференцируя 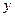 как сложную функцию получим
как сложную функцию получим
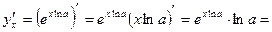
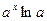
3. Логарифмическая функция 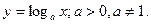
Найдем сначала производную от 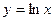
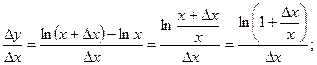
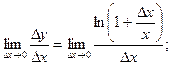 Поскольку
Поскольку 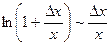
 при
при 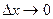 полчучим:
полчучим:
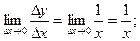 т.е.
т.е. 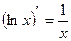 но т.к.
но т.к.
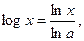 то
то 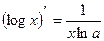
4. Тригонометрические функции.
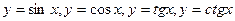
Для 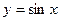 имеем
имеем 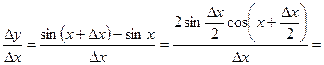
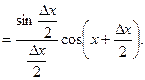
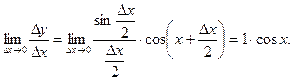
Т.е. 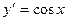 или
или 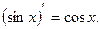
Проделав аналогичные преобразования можно получить:
а) 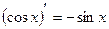
б) 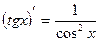
в) 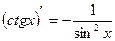
5. Точно таким же образом находятся формулы для расчета производных обратных тригонометрических функций.
а) 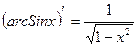
б) 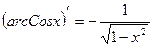
в) 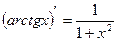
г) 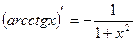
Обобщив все полученные выше правила и выведенные соотношения можно получить так называемую таблицу производных:
6) Таблица дифференцирования:
1. 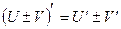
2. 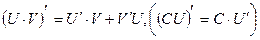
3. 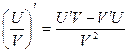 ;
; 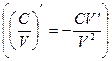
4. 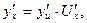 если
если 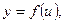 а
а 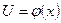
5. 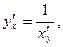 если
если 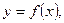 а
а 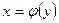
Формулы дифференцирования:
1. 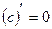
2. 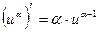
3. 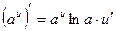
4. 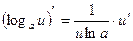
5. 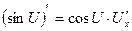
6. 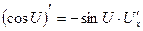
7. 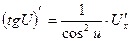
8. 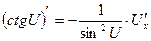
9. 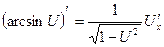
10. 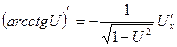
11. 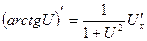
12. 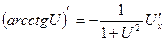
7) Дифференцирование неявных и параметрических заданных функций.
1) Если функция задана уравнением y=f(x), решенным относительно y, то функция задана в явном виде(явная функция). Под неявным заданием функции понимают задание функции в виде уравнения F(x,y)=0 не разрешенного относительно y. Всякую явно заданную функцию можно записать как неявно заданную уравнением F(x)-y=0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно y (например: y+2x+cosy-1=0). Если неявная функция задана уравнением F(x,y)=0, то для нахождения производной y по x нет необходимости разрешать уравнение относительно y. Достаточно продифференцировать это уравнение по x, рассматривая при этом y как функцию x, и полученное затем уравнение разрешить относительно 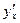 . Производная неявной функции выражается через аргумент x и функцию y.
. Производная неявной функции выражается через аргумент x и функцию y.
Пример: найти производную функции y заданную уравнением : 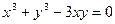
Дифференцируя по, x получим: 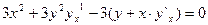
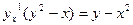 , т.е.
, т.е. 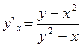 ;
;
2. Функция заданная параметрически. Пусть зависимость между аргументом x и функцией y задана параметрически в виде уравнений
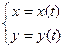
где t- вспомогательная переменная, называемая параметром.
Найдем y'x , считая, что записанные функции имеют производные и что функция x=x(t) имеет обратную функцию t=φ(x). По правилу дифференцирования обратной функции
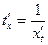
Функцию y=f(x) можно рассматривать как сложную функцию y=y(t), где t=φ(x), тогда по правилу дифференцирования сложной функции
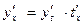
Или
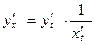
т.е.

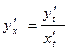
Полученное соотношение позволяет находить производную y'x от функции заданной параметрически, не находя непосредственную зависимость y от x.
Пример :
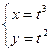 найти
найти 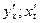
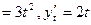 .Тогда
.Тогда 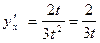
В правильности полученного соотношения легко убедиться. Действительно 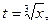 тогда
тогда 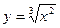 отсюда
отсюда 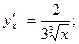 т.е.
т.е. 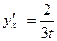
8) Логарифмическое дифференцирование
В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать, а затем результат продифференцировать.
Такую операцию и называют логарифмическим дифференцированием.
Пример: найти производную функции:
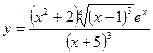
Прологарифмируя это соотношение, получим:
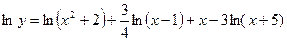
Дифференцируя по x получим : 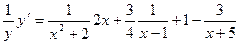
Найдем 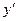 =y
=y 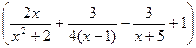
или
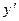 =
= 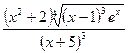
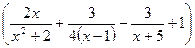 ;
;
Существуют функции производные, которых можно найти лишь логарифмическим дифференцированием. К их числу относятся так называемые степенно-показательные функции: y= 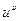 , где u=u(x) и
, где u=u(x) и 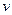 =
= 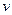 (x). Найдем производную этой функции
(x). Найдем производную этой функции 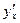 . Логарифмируем:
. Логарифмируем:
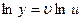
Дифференцируем: 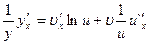
Или 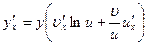
Или 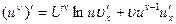 .
.
9) Производные высших порядков
1. Производные высших порядков явно заданной функции.
Производная y'x=f '(x) функции y=f(x), есть также функция от x и называется производной первого порядка. Если функция 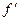 (x) дифференцируема, то ее производная называется производной второго порядка и обозначается :
(x) дифференцируема, то ее производная называется производной второго порядка и обозначается :
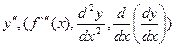
Итак, y''=(y')'.
Производной от y'', если она существует, называется производной третьего порядка y'''=(y'')' и т.д.
Производной n-го порядка называется производная от производной (n-1) порядка
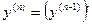
Производные порядка выше первого называются производными высших порядков.
Смысл производной второго порядка ( механический)
Рассмотрим ту же задачу, которую мы рассматривали для определения механического смысла первой производной.
Точка M движется по произвольной линии тогда:
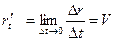 (мгновенная скорость точки в данный момент времени).
(мгновенная скорость точки в данный момент времени).
Пусть в момент времени t, скорость равна V, а в момент t+∆t скорость равно V+∆V,тогда
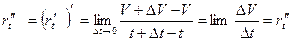
- эта величина показывает изменение скорости за сколько угодно малый промежуток времени и в механике она называется ускорением в данный момент времени.
2. Производные высших порядков неявно заданной функции.
Пустьy=f(x) задана неявно F(x,y)=0. Продифференцировав это уравнение по x, и разрешив относительно y' найдем первую производную. Продифференцировав еще раз найдем вторую и т.д.
3. Производные высших порядков от функции заданной параметрически
Пусть y=f(x) задана параметрически:
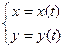
Как известно y'x = 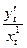 . Найдем y''x .
. Найдем y''x .
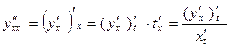
Т.к. 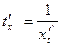 как обратные функции ,то
как обратные функции ,то 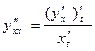
10) Дифференциал функции
Пусть функция y=f(x) имеет в точке x отличную от нуля производную f '(x)≠0, тогда по теореме о связи функции, ее пределом и бесконечно малой функции можно записать
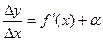 ,где α→0 при ∆x→0 или
,где α→0 при ∆x→0 или
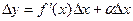
Таким образом, приращение функции ∆y представляет собой сумму двух слагаемых f '(x)∆x и α∆x являющихся бесконечно малыми при ∆x→0. при этом первое слагаемое есть бесконечно малая функция одного порядка с ∆x, так как
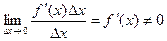 , а второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆x:
, а второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆x:
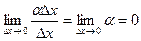
Поэтому первое слагаемое f '(x)∆x называют главной частью приращения функции ∆y.
Дифференциалом функции y=f(x) в точке x и называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy(или d(f(x)). По определению: dy= 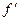 (x)dx
(x)dx
Иными словами.
Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Пример: найти дифференциал 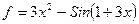
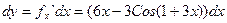
11) .Геометрический смысл дифференциала функции
|
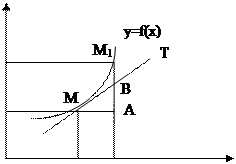 Проведем к графику y=f(x) в точке M(x,y) касательную MT и рассмотрим ординату этой касательной для точки x+∆x (рис.7). На рисунке |AM|=∆x, |AM1|=∆y из ∆MAB имеем
Проведем к графику y=f(x) в точке M(x,y) касательную MT и рассмотрим ординату этой касательной для точки x+∆x (рис.7). На рисунке |AM|=∆x, |AM1|=∆y из ∆MAB имеем
|
|
|
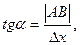
|
|
|
|
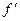 (x)∆x.
(x)∆x. Сравнивая полученный результат с определением дифференциала, получаем dy=AB, т.е. дифференциал функции в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получит приращение ∆x.
12) Основные теоремы о дифференциалах
Они вытекают из теоремы о производных. Например, т.к. y'=0 при y=c, то дифференциал постоянной величины c тоже равен нулю dy=c'dx=0.
Теорема 1. дифференциал суммы, произведения и частного двух дифференцируемых функций определяется следующими формулами
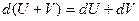
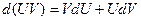
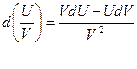 при V≠0
при V≠0
Докажем, например, правильность второй формулы. По определению дифференциала имеем:
d(UV)=(UV)'dx=(U'V+UV')dx=VU'dx+UV'dx=Vdu+Udv
Теорема 2. дифференциал сложной функции равен произведению этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
Пусть y=f(u) и u=φ(x)- две дифференцируемые функции образующие сложную функцию: y=f(φ(x)). По теореме о производной сложной функции можно написать y'x=y'uu'x. Умножив обе части этого равенства на dx, получим: y'xdx=dy=y'uu'xdx, учитывая, что u'xdx=du, получим: dy=y'udu. Итак, дифференциал определяется одной и той же формулой, не зависимо от того, является ли ее аргумент независимой переменной или нет.
Это свойство дифференциала называют инвариантностью (неизменностью) формы первого дифференциала. При этом необходимо учитывать, что если dx= 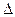 x, то u есть функция от x, поэтому, вообще говоря, du≠∆u.
x, то u есть функция от x, поэтому, вообще говоря, du≠∆u.
С помощью определения дифференциала можно легко преобразовать таблицу производных в таблицу дифференциалов:
1) 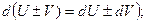
2)d(UV)=VdU+Ud 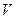 , в частности d(CU)=CdU
, в частности d(CU)=CdU
3) 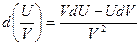 , в частности d
, в частности d 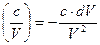 и т.д.
и т.д.
13) Применение дифференциала к приближенным вычислениям.
Как говорилось выше, приращение функции ∆y в точке x можно представить в виде ∆y= 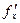 (x)∆x+α∆x, где α→0 при x→0, или ∆y=dy+α∆x. Отбрасывая бесконечно малую величину α∆x более высокого порядка, чем ∆x, получим приближенное равенство: ∆y≈ dy. Причем это равенство тем точнее, чем меньше ∆x.
(x)∆x+α∆x, где α→0 при x→0, или ∆y=dy+α∆x. Отбрасывая бесконечно малую величину α∆x более высокого порядка, чем ∆x, получим приближенное равенство: ∆y≈ dy. Причем это равенство тем точнее, чем меньше ∆x.
Это равенство позволяет с большой точностью вычислять приближенно приращение любой дифференцируемой функции. Дифференциал обычно находится значительно проще, поэтому это соотношение широко применяется на практике.
Пример: найти приближенное значение функции 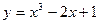 , при x=2 и ∆x=0,001.
, при x=2 и ∆x=0,001.
Решение: 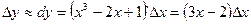
dy= 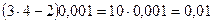 . Итак,
. Итак, 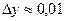
Определим, какую погрешность мы допустили при этом приближенном вычислении. Для этого найдем точное значение ∆y
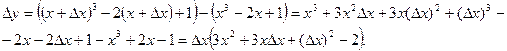
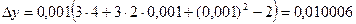
Абсолютная погрешность составит
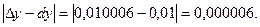
Формулу приближенных соотношений обычно записывают в виде:
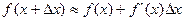
14) Дифференциалы высших порядков
Пусть функция y=f(x)- дифференцируемая функция, а ее аргумент x- независимая переменная. Тогда ее первый дифференциал dy=f '(x)dx есть также функция x и можно найти дифференциал этой функции .
Дифференциал от дифференциала функции y=f(x) называется дифференциалом второго порядка (вторым дифференциалом) обозначается d2y=d(dy).
Итак, по определению d2y=d(dy). Найдем выражение для d2y. Так как dx=∆x не зависит от x, то при дифференцировании считаем dx- const:
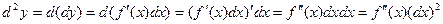
Т.е. 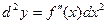
Аналогично можно записать, что дифференциал n-го порядка определяется согласно соотношению:
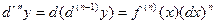
Т.е. дифференциал второго порядка и (вообще n-го) порядка равен произведению производной второго порядка (n-го) на квадрат (n-ю степень) дифференциала независимой переменной.
Из этих соотношений следует, что

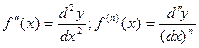
В заключении отметим, что эти соотношения справедливы только в случае если
x-независимая переменная. Если же y=f(x), где x- функция другого аргумента, то дифференциалы высших порядков (n>1) не обладают свойством инвариантности и вычисляются по другим формулам.
6. Исследование функций с помощью методов дифференциального исчисления.
1) Основные теоремы о дифференцируемых функциях.
Теорема 1. (Ролля) Если f(x) непрерывна на [  ,b] и дифференцируема на интервале (
,b] и дифференцируема на интервале (  ,b) и на концах отрезка принимает одинаковые значения f(
,b) и на концах отрезка принимает одинаковые значения f(  )=f(b), то найдется хотя бы одна точка С
)=f(b), то найдется хотя бы одна точка С 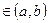 в которой f '(x)=0, т.е. f '(c)=0.
в которой f '(x)=0, т.е. f '(c)=0.
Так как функция f(х) непрерывна на [  ,b], то она достигает на этом отрезке своего наибольшего и наименьшего значения соответственно М и m. Если М
,b], то она достигает на этом отрезке своего наибольшего и наименьшего значения соответственно М и m. Если М 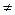 m, f(x)= const на [
m, f(x)= const на [  ,b] и следовательно
,b] и следовательно 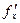 =0 в любой точке [
=0 в любой точке [  ,b]. Если М ≠ m, то функция достигает хотя бы одно из значений М или m во внутренней точки С интервала [
,b]. Если М ≠ m, то функция достигает хотя бы одно из значений М или m во внутренней точки С интервала [  ,b], так как f(
,b], так как f(  )=f(b). Пусть например, функция принимает значение М в точке
)=f(b). Пусть например, функция принимает значение М в точке 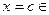 (
(  ,b), т.е. f(с)=М, тогда для всех
,b), т.е. f(с)=М, тогда для всех 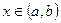 выполняется соотношение
выполняется соотношение 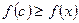 Найдем
Найдем 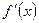 в точке х=с.
в точке х=с. 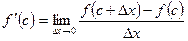 В силу неравенства f(x)< f (с),
В силу неравенства f(x)< f (с), 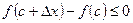 , если
, если 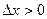 т.е.
т.е. 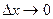 справа от точки
справа от точки 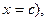 то
то 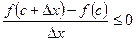 и
и 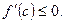 Если
Если 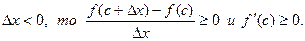
Таким образом f '(с) =0. В случае, когда 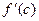 = m доказательство носит аналогичный характер.
= m доказательство носит аналогичный характер.
Геометрически теорема Ролля означает, что на графике функции y=f'(х) найдется точка в которой касательная параллельна к графику параллельна оси ох. (рис.8.)
 | |||||||||||
 |  | ||||||||||
 | |||||||||||
| |||||||||||
| |||||||||||


|
|
 | |||||
|
| ||||
|
|