Прямые второго порядка
Задачи
Векторы. Основные понятия.
1)Действия над векторами
1. Вычислить модуль вектора  ={6; 3; -2}.
={6; 3; -2}.
2. Даны точки A(3; -1; 2), B(-1; 2; 1). Найти координаты векторов  и
и 
3. Определить точку N, с которой совпадает конец вектора  ={3; -1; 4}, если его начало совпадает с точкой М(1; 2; -3)
={3; -1; 4}, если его начало совпадает с точкой М(1; 2; -3)
2)Проекция вектора на оси
1. Дан модуль вектора  =2 и углы
=2 и углы  =450,
=450,  =600,
=600, 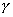 =1200. Вычислить проекции вектора
=1200. Вычислить проекции вектора  на координатные оси
на координатные оси
2. Вычислить направляющие косинусы вектора  ={12; -15; -16}
={12; -15; -16}
3. Даны два вектора  ={3; -2; 6},
={3; -2; 6},  ={-2; 1; 0}. Определить проекции на координатные оси следующих векторов:
={-2; 1; 0}. Определить проекции на координатные оси следующих векторов:
А)  б)
б) 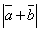 в)
в)  г)
г)  д)
д) 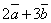
3)Разложение вектора по координатам
1. Три силы  ,
, 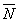 ,
, 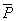 , приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их равнодействующей
, приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их равнодействующей  ,если известно, что
,если известно, что 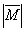 =2Н,
=2Н,  =10Н,
=10Н, 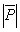 =11Н
=11Н
2. На плоскости даны три вектора  ={3; -2},
={3; -2},  ={-2; 1},
={-2; 1}, 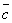 ={7; -4}. Определить разложение каждого из этих трех векторов, принимая в качестве базиса два других
={7; -4}. Определить разложение каждого из этих трех векторов, принимая в качестве базиса два других
3. На плоскости даны два вектора 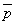 ={2; -3},
={2; -3}, 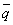 ={1; 2}. Найи разложение вектора
={1; 2}. Найи разложение вектора  ={9; 4} по базису
={9; 4} по базису 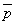 ,
, 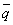
4. Может ли вектор составлять с координатными осями следующие углы:
А)  =450,
=450,  =600,
=600, 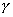 =120
=120
Б)  =450,
=450,  =1350,
=1350, 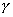 =600
=600
В)  =900,
=900,  =1500,
=1500, 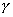 =600
=600
4)Скалярное произведение векторов
1. Даны  =13,
=13, 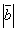 =19 и
=19 и 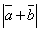 =24. Вычислить
=24. Вычислить 
2. Векторы  и
и  взаимно перпендикулярны, причем
взаимно перпендикулярны, причем  =5,
=5, 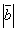 =12. Определить
=12. Определить 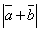 и
и 
3. Векторы  и
и  образуют угол
образуют угол 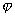 =1200, причем
=1200, причем  =3 и
=3 и 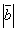 =5. Определить
=5. Определить 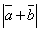 и
и 
4. Даны векторы  ,
,  ,
, 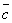 , удовлетворяющие условию
, удовлетворяющие условию 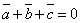 . Зная, что
. Зная, что  =3,
=3, 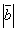 =1,
=1, 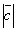 =4, вычислить
=4, вычислить 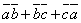
5. Векторы  и
и  образуют угол
образуют угол 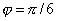 ; зная, что
; зная, что  ,
, 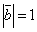 , вычислить угол
, вычислить угол  между векторами
между векторами 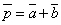 и
и 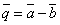
6. Векторы  и
и  образуют угол
образуют угол  , зная, что
, зная, что  =3,
=3, 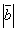 =4, вычислить
=4, вычислить
А)  б)
б) 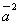 в)
в) 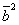 г)
г)  д)
д) 
5)Векторное произведение координат
1. Векторы  и
и  образуют угол
образуют угол 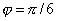 . Зная, что
. Зная, что  =6 и
=6 и 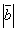 =5, вычислить
=5, вычислить 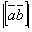
2. Векторы  и
и  взаимно перпендикулярные. Зная, что :
взаимно перпендикулярные. Зная, что :  =3,
=3, 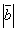 =4, вычислить: а)
=4, вычислить: а) 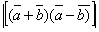 , б)
, б) 
3. Сила 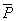 ={2; 2; 9} приложена к точке А(4; 2; -3). Определить величину и направляющие косинусы момента этой силы относительно точки С(2; 4; 0)
={2; 2; 9} приложена к точке А(4; 2; -3). Определить величину и направляющие косинусы момента этой силы относительно точки С(2; 4; 0)
6)Выражение скалярного произведения через координаты векторов
1. Вычислить косинус угла, образованного векторами а={2; -4; 4} и б={-3; 2; -6}
2. Даны векторы  ={4; -2; -4},
={4; -2; -4},  ={6; -3; 2}. Вычислить:
={6; -3; 2}. Вычислить:
А)  б)
б)  в)
в)  г)
г) 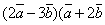 д)
д)  е)
е) 
7)Установление коллинеарности векторов
1. Проверить коллинеарность векторов  ={2; -1; 3} и
={2; -1; 3} и  ={-6; 3; -9}
={-6; 3; -9}
2. Определить, при каких значениях  ,
,  векторы
векторы  и
и  коллинеарны.
коллинеарны.
3. Даны точки A(-1; 5; -10}, B(5; -7; 8), C(2; 2; -7), D(5; -4; 2). Проверить, что векторы  и
и 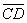 коллинеарны
коллинеарны
8)Нахождение линейной скорости вращения
1. Векторы  ,
,  ,
, 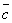 , образующие правую тройку, взаимно перпендикулярны. Зная, что
, образующие правую тройку, взаимно перпендикулярны. Зная, что  ,
, 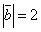 ,
,  , вычислить
, вычислить 
2. Установить, компланарны ли векторы  ,
,  ,
, 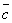 , если:
, если:
а)  ={2; 3; -1},
={2; 3; -1},  ={1; -1; 3},
={1; -1; 3}, 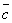 ={1; 9; -11}
={1; 9; -11}
б)  ={3; -2; 1},
={3; -2; 1},  ={2; 1; 2},
={2; 1; 2}, 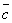 ={3; -1; -2};
={3; -1; -2};
в)  ={2; -1; 2},
={2; -1; 2},  ={1; 2; -3},
={1; 2; -3}, 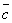 ={3; -4; 7}
={3; -4; 7}
- Матрицы
1)Произведение матрицы на матрицу
1) Решить f=A*A*A-3A*A+1 если А 
2) Умножить матрицу А  на В
на В 
2)Определитель матрицы
1. Определить, при каких значениях a и b система уравнений 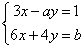 : 1). Имеет единственно решение, 2). Не имеет решений, 3). Имеет бесконечно много решений.
: 1). Имеет единственно решение, 2). Не имеет решений, 3). Имеет бесконечно много решений.
2. Вычислить определители третьего порядка:
1)  2)
2)  3)
3) 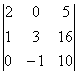
3. Найти все решения каждой из следующих систем уравнений
1) 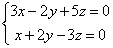 2)
2)  3)
3) 
4. Найти единственное решение систем:
1) 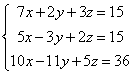 2)
2) 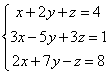
3)Вычисление обратной матрицы
1) Решить АХ=В, если 1.  2.
2. 
4)Метод Гауса
1) Решить системы методом Гауса
 2a+ 2a+ | 3b+ | 14c+ | 13d=0 |
| 2d+ | 8c+ | 2d=0 | |
| -4a+ | 2d+ | 4c- | 18d=0 |
| -2a+ | b+ | 2c- | 9d=0 |
2)
 -5a+ -5a+ | 5b+ | d=0 | |
| 3a+ | 2d+ | c- | 2d=0 |
| a+ | d- | c+ | d=0 |
| a+ | c | =0 |
- Аналитическая геометрия на плоскости
1)Преобразования системы координат
1. Начало координат перенесено (без изменения направления осей) в точку O’(3; -4). Координаты точек А(1; 3), B(-3; 0), C(-1; 4) определены в новой системе. Вычислить координаты этих же точек в старой системе координат.
2. Написать формулы преобразований координат, если начало координат (без изменения направления осей) перенесено в точку: а) А(3; 4) б) B(-2; 1) в) C(-3; 5)
2)Преобразование системы координат с помощью поворота
1) Написать формулы преобразований координат, если координатные оси повернуты на один из следующих углов: а) 60 б) -45 в) 90 г) -90 д)180
2) Координатные оси повернуты на угол 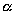 =600. Координаты точек А(
=600. Координаты точек А(  ; -4), B(
; -4), B( 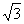 ; 0), C(0;
; 0), C(0;  ) определены в новой системе. Вычислить координаты этих же точек в старой системе.
) определены в новой системе. Вычислить координаты этих же точек в старой системе.
3)Общее равнение прямой
1) Найти точку пересечения двух прямых  ,
, 
2) Стороны АВ, ВС и АС треугольника АВС даны соответственно уравнениями  ,
, 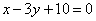 ,
, 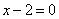 . Определить координаты его вершин
. Определить координаты его вершин
3) Составить уравнение прямой и построить прямую на чертеже, зная ее угловой коэффициент k и отрезок b, отсекаемый ею на оси Oy: а) k=3, b=0; б) k=-2, b=-5; в) k=0, b=-2;
4)Уравнение прямой, проходящей через две точки. Уравнение прямой, проходящей через заданную точку и перпендикулярной заданному вектору.
1) Даны вершины треугольника M1(2; 1), M2(-1; -1), M3(3; 2). Составить уравнения его высот.
2) Даны вершины треугольника A(1; -1), B(-2; 1), C(3; 5). Составить уравнение перпендикуляра, опущенного из вершины А на медиану, проведенную из вершины В.
3) На прямой 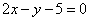 найти такую точку Р, сумма расстояний которой до точек A(-7; 1), B(-5; 5) была бы наименьшей.
найти такую точку Р, сумма расстояний которой до точек A(-7; 1), B(-5; 5) была бы наименьшей.
4) Даны две вершины A(3; -1), B(5; 7) треугольника ABC и точка N(4; -1) пересечения его высот. Составить уравнения сторон этого треугольника
Прямые второго порядка
1)Эллипс
1. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, зная, кроме того, что: а) его малая ось равна 6, а расстояние между директрисами равно 13 ; б) его большая ось равна 20, а эксцентриситет e=3/5 Ж; в) его большая ось равна 10, а расстояние между фокусами 2c=8.
2. Установить, что следующее уравнение определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет и уравнения директрис: 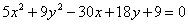
3. Дан эллипс 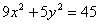 . Найти его полуоси, фокусы, эксцентриситет, уравнения директрис.
. Найти его полуоси, фокусы, эксцентриситет, уравнения директрис.
4. Точка M1(3; -1) является концом малой оси эллипса, фокусы которого лежат на прямой 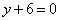 . Составить уравнение этого эллипса, зная его эксцентриситет e=
. Составить уравнение этого эллипса, зная его эксцентриситет e=  .
.
2)Гипербола
1. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, кроме того, что: а) расстояние между фокусами 2c=10 и ось 2b=8; б) расстояние между директрисами равно 228/13 и расстояние между фокусами 2c=26; в) ось 2a=16 и эксцентриситет e=5/4
2. Дана гипербола  . Найти: полуоси а и b, фокусы, эксцентриситет, уравнения асимптот, уравнения директрис
. Найти: полуоси а и b, фокусы, эксцентриситет, уравнения асимптот, уравнения директрис
3. Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс симметрично относительно начала координат, если даны точки M1(6; -1), M2(-8;  ) гиперболы
) гиперболы
4. Привести ур-е к каноническому виду; определить тип; установить, какой геометрический образ определяет; изобразить на чертеже оси первоначальной координатной системы; оси других координатных систем, которые вводятся по ходу решению, и геометрический образ, определяемый данным уравнением:
1) 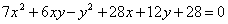 2)
2) 
3)Парабола
1. Составить уравнение параболы, вершина которой находится в начале координат, зная, что: а) парабола расположена в правой полуплоскости, симметрично относительно оси Ох и ее параметр р=3; б) парабола расположена в левой полуплоскости симетрично относительно оси Ох и ее параметр р=0,5 ; в) парабола расположена в нижней полуплоскости симметрично оси Оу и ее параметр р=3.
2. Даны вершина параболы А(6; -3) и уравнение ее директрисы  . Найти фокус F этой параболы.
. Найти фокус F этой параболы.
3. Даны вершина параболы А(-2; -1) и уравнение е директрисы 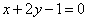 . Составить уравнение этой параболы.
. Составить уравнение этой параболы.
4. Привести ур-е к каноническому виду; определить тип; установить, какой геометрический образ определяет; изобразить на чертеже оси первоначальной координатной системы; оси других координатных систем, которые вводятся по ходу решению, и геометрический образ, определяемый данным уравнением:
1) 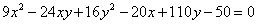
2) 
