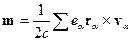Функция Грина в случае неограниченной области
Физические основы фотоники
(конспект лекций для ЭКТ-2М)
Г.
Оглавление
1 § 1. Плотность заряда и её вид в случае системы точечных зарядов. Уравнения Максвелла для электромагнитного поля в вакууме. 4
2 § 2. Закон сохранения заряда [в форме уравнения непрерывности]. Теорема Остроградского-Гаусса 5
3 § 3. Потенциалы электромагнитного поля в вакууме. Градиентная инвариантность. 6
4 § 4. Типы калибровок. 6
5 § 5. [Микро- и макро-] уравнения Максвелла для электромагнитного поля в среде. Потенциалы электромагнитного поля в среде. 9
6 § 6. [Калибровка Лоренца в случае однородной изотропной среды]. Уравнение Даламбера (без учёта пространственной дисперсии) 11
7 § 7. Уравнения Максвелла для стационарного электромагнитного поля в среде. Уравнения Пуассона в электростатике. 12
§ 8. Функция Грина в случае неограниченной области. 13
8 § 9. [Оператор трансляции]. Потенциал системы зарядов. 14
9 § 10. Электрические (дипольный [и квадрупольный]) моменты системы зарядов. [Магнитный дипольный момент системы токов.] 16
§ 11. Электрическое поле системы зарядов на больших расстояниях. 17
§ 12. Система зарядов во внешнем электростатическом поле. 19
10 § 13. Векторный потенциал системы стационарных токов. Приближение линейного тока. 20
11 § 14. Уравнения Максвелла для квазистационарного электромагнитного поля. [Условия квазистационарности поля.] 22
12 § 15. Глубина проникновения квазистационарного электромагнитного поля. 23
13 § 16. Уравнения Максвелла электромагнитных волн в вакууме. Волновое уравнение в случае вакуума. 25
§ 17. Решение волнового уравнения в случае плоской электромагнитной волны в вакууме. 25
14 § 18. Плоская монохроматическая волна. Уравнения Максвелла в случае плоской монохроматической волны в вакууме. [Разложение электромагнитных полей по плоским монохроматическим волнам.] 27
§ 19. Теорема Пойнтинга (Закон сохранения энергии электромагнитных волн в форме уравнения непрерывности). Теорема Пойнтинга с учётом диссипации для среды.. 29
15 § 20. Соотношение между векторами 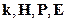 в случае плоских электромагнитных волн в вакууме 30
в случае плоских электромагнитных волн в вакууме 30
§ 21. Функция Грина уравнения Гельмгольца. 31
§ 22. Запаздывающая функция Грина уравнения Даламбера. 33
§ 23. Пространственно-временная дисперсия в электродинамике. Уравнения Максвелла для электромагнитного поля в среде с пространственно-временной дисперсией. 35
16 § 24. Волновое уравнение в случае среды с пространственной дисперсией. 36
17 § 25. Групповая скорость. 37
18 § 26. Метод самосогласования. Использование метода самосогласования для нахождения электростатического потенциала в плазме. Дебаевский радиус экранирования. 38
19 § 27. Запаздывающие потенциалы. Разложение запаздывающих потенциалов в ряды по малому параметру. 41
20 § 28. Дипольное излучение. Волновая зона дипольного излучения. 43
21 § 29. Интенсивность дипольного излучения в волновой зоне. Примеры (задачи №23 и №28) 45
§ 30. Материальные уравнения или уравнения связи. 47
22 § 31. Поведение электромагнитного поля при переходе через границу раздела двух сред. 49
§ 32. Краевые, граничные условия. Задачи Дирихле и Неймана. Функция Грина задач электростатики. 52
§ 33. Физический смысл функции Грина. Теорема взаимности в электростатике. 53
Факультатив. 55
1 § 1. Тензоры 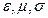 и их свойства. Симметрия кристаллов. 55
и их свойства. Симметрия кристаллов. 55
§ 2. Поверхностная плотность зарядов на границе раздела двух поляризованных диэлектриков 56
§ 3. Электрический дипольный момент поляризованного диэлектрика. Роль поверхностных зарядов. 57
§ 4. Электрическое поле поляризованного диэлектрика. Поле диполя. 58
§ 5. Случай однородно-поляризованного диэлектрика. Задача о расчёте поля внутри эллипсоидальной полости в однородно-поляризованном диэлектрике. 59
§ 6. Энергия взаимодействия двух электрических мульти-полей. 61
2 § 7. Дисперсионное уравнение. Нормальные электромагнитные волны в неограниченной среде 62
3 § 8. Поперечные и продольные нормальные волны в среде. Решение дисперсионного уравнения в случае однородной и изотропной среды с пространственной дисперсией. 63
§ 9. Калибровка Лоренца в случае запаздывающих потенциалов. 64
§ 10. Ближняя зона дипольного излучения. 66
§ 11. Теорема взаимности в теории излучения. 67
§ 12. Уравнения Максвелла для электромагнитного поля в среде с учетом пространственно-временной дисперсии. Соотношения Линдхарда. 69
§ 13. Нормальные волны.. 72
§ 14. Неоднородные среды.. 73
§ 15. Электромагнитные волны в немагнитных анизотропных средах. 74
§ 16. Рассеяние электромагнитных волн в неоднородных средах. 80
§ 17. Статистическое описание неоднородных сред. 81
§ 18. Вычисление моментов 1-го и 2-го порядков в случае многокомпонентной смеси изотропных компонентов. 82
§ 19. Решение волнового уравнения в случае неоднородной среды.. 83
§ 20. Расчет показателя рассеяния 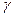 , фазовой
, фазовой 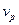 и групповой
и групповой 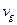 скорости электромагнитных волн в неоднородных средах. 84
скорости электромагнитных волн в неоднородных средах. 84
§ 21. Асимптотические выражения для показателя рассеяния 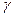 .. 85
.. 85
§ 22. Поверхностный импеданс металлов. 86
§ 23. Граничное условие Леонтовича. 87
§ 24. Случай идеального проводника. 88
§ 25. Электромагнитное поле в пространстве между двумя неограниченными плоскопараллельными идеально-проводящими плоскостями. 89
§ 26. Полные электромагнитные резонаторы.. 90
§ 27. Распространение электромагнитных волн в волноводах. 91
Дополнение 1. Метаматериалы.. 93
Задачи по курсу «Физические основы фотоники» и их решения. 104
Задачи по курсу «Физические основы фотоники». 155
Задачи по курсу «Физические основы фотоники» (минимум) 165
Вопросы по курсу «Физические основы фотоники». 168
Вопросы по курсу «Физические основы фотоники» (минимум) 169
Список литературы.. 170
Основная литература. 170
Дополнительная литература. 170
1 § 1. Плотность заряда и её вид в случае системы точечных зарядов. Уравнения Максвелла для электромагнитного поля в вакууме
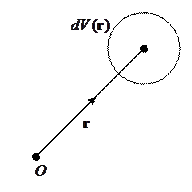
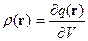
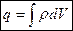
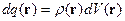
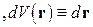
Рассмотрим систему из точеченого заряда 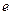
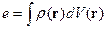
 Здесь возникает необходимость использовать
Здесь возникает необходимость использовать 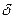 -функцию.
-функцию.
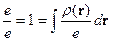
Тогда 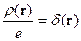
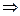
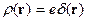 .
.
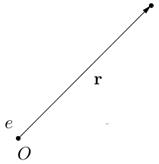
Это соответствует случаю, когда заряд помещён в начало координат, а плотность заряда ищется в точке, с радиус-вектором 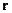 .
.
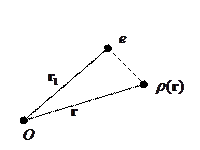
Если же заряд помещён не в начало отсчёта, то плотность заряда перепишется в следующем виде:
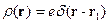
В случае системы точечных зарядов имеем:
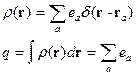
Нужно отметить, что всегда для изображения плотности точечного источника используется 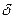 -функция.
-функция.
Будем использовать гауссову систему:
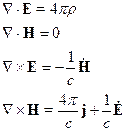
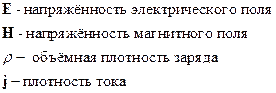

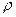 и
и 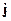 являются источниками поля. Уравнения Максвелла позволяют по заданным источникам рассчитать электромагнитное поле. Уравнениям Максвелла в дифференциальной форме ставятся в соответствие уравнения в интегральной форме.
являются источниками поля. Уравнения Максвелла позволяют по заданным источникам рассчитать электромагнитное поле. Уравнениям Максвелла в дифференциальной форме ставятся в соответствие уравнения в интегральной форме.
2 § 2. Закон сохранения заряда [в форме уравнения непрерывности]. Теорема Остроградского-Гаусса
Запишем уравнение Максвелла: 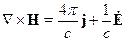 . Подействуем на него оператором
. Подействуем на него оператором 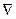 скалярно. Получаем:
скалярно. Получаем:
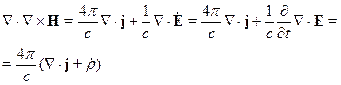
Но дивергенция всякого ротора равна нулю, поэтому в результате получаем:
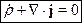 - уравнение непрерывности
- уравнение непрерывности
Проинтегрируем обе части этого уравнения по некоторому объёму:

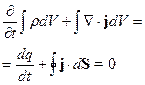
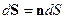 , где
, где 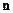 -единичный вектор нормали
-единичный вектор нормали
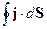 определяет количество заряда выносимого через поверхность объёма. Если
определяет количество заряда выносимого через поверхность объёма. Если 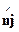 - острый, то заряд выносится из объёма и
- острый, то заряд выносится из объёма и 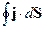 -положителен. Если
-положителен. Если 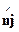 тупой, то заряд приходит в объём и
тупой, то заряд приходит в объём и 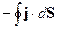 - имеет знак минус.
- имеет знак минус.
Теорема Остроградского-Гаусса:
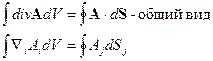
Перейдём к тензорам второго ранга 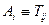 . Получим:
. Получим:

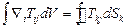
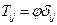 (
( 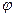 - скалярная функция), тогда:
- скалярная функция), тогда:
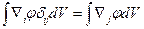
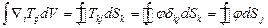
В результате получаем:
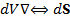 - более общая модификация теоремы Остроградского-Гаусса.
- более общая модификация теоремы Остроградского-Гаусса.
3 § 3. Потенциалы электромагнитного поля в вакууме. Градиентная инвариантность
Удобно ввести:
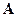 -векторный потенциал
-векторный потенциал
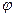 -скалярный потенциал
-скалярный потенциал
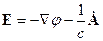
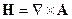
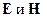 однозначно определяют электромагнитное поле
однозначно определяют электромагнитное поле
Существует преобразование, которое не меняет полевых характеристик 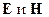 . Таким преобразованием является градиентное:
. Таким преобразованием является градиентное:
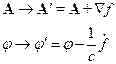
Здесь 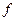 – произвольная функция координат и времени
– произвольная функция координат и времени 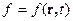
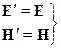 -инвариантность полевых характеристик
-инвариантность полевых характеристик
относительно градиентных преобразований.
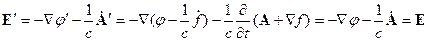
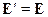
Аналогично для 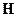 :
:
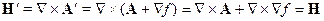
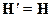
На потенциалы 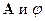 могут быть наложены произвольные, удобные для исследования ограничения – калибровки потенциалов, т.к.
могут быть наложены произвольные, удобные для исследования ограничения – калибровки потенциалов, т.к. 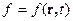 - произвольная.
- произвольная.
4 § 4. Типы калибровок
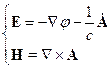
Перепишем уравнения Максвелла:

1.
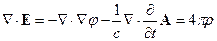 (4.1)
(4.1)
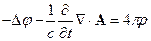
2.
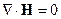
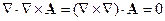
3.
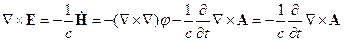
4.
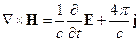
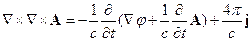 (4.2)
(4.2)
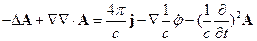

1.Калибровка Лоренца
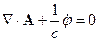
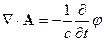
Тогда уравнение (4.1) перепишется в следующем виде:
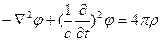
ð 
ð 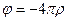 - уравнение Даламбера
- уравнение Даламбера
Это уравнение есть – неоднородное дифференциальное уравнение в частных производных.
ð - оператор гиперболического типа.
Для уравнения (4.2) имеем:
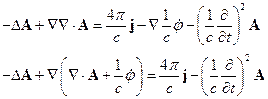
ð 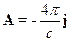
Все, имеющие физический смысл, результаты должны быть градиентно-инвариантными:
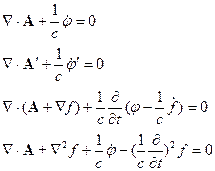
В силу калибровки Лоренца получаем:
ð 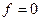
Т.е. функция 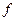 должна удовлетворять однородному уравнению Даламбера (его ещё называют волновым уравнением)
должна удовлетворять однородному уравнению Даламбера (его ещё называют волновым уравнением)
2.Калибровка Кулона
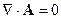 - калибровка Кулона
- калибровка Кулона
Уравнение (4.1) перепишется в следующем виде:
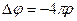 - уравнение Пуассона.
- уравнение Пуассона.
Если же 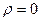 (в пустоте), то уравнение Пуассона принимает вид:
(в пустоте), то уравнение Пуассона принимает вид:
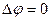 -уравнение Лапласа.
-уравнение Лапласа.
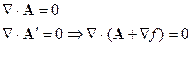
получаем, что функция 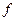 должна удовлетворять уравнению:
должна удовлетворять уравнению:
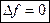
3.Калибровка поперечных волн
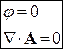
Полагаем 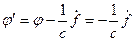
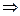
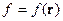 есть функция только координат.
есть функция только координат.
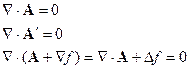
Значит функция 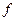 должна удовлетворять уравнению:
должна удовлетворять уравнению:
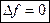
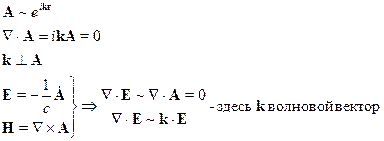
5 § 5. [Микро- и макро-] уравнения Максвелла для электромагнитного поля в среде. Потенциалы электромагнитного поля в среде
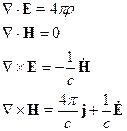
С помощью этих уравнений можно описывать электромагнитное поле в среде. В среде будем ставить индекс « 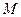 »=микро
»=микро
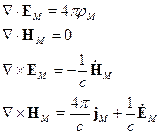
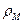 включает в себя как связанные, так и свободные заряды в веществе. Каждой точке пространства ставится в соответствие функция
включает в себя как связанные, так и свободные заряды в веществе. Каждой точке пространства ставится в соответствие функция 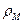 . Это значит, что мы заменяем реальную среду моделью – сплошной средой, т.е. мы свойства разных точек «размазываем» по пространству. Существуют следующие способы описания сплошной среды на основе реальной среды:
. Это значит, что мы заменяем реальную среду моделью – сплошной средой, т.е. мы свойства разных точек «размазываем» по пространству. Существуют следующие способы описания сплошной среды на основе реальной среды:
1. Усреднение по некоторому физическому объёму 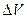 и времени
и времени 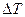 .
.
2. Статистическое усреднение. Считаем, что у нас есть макроскопически идентичный ансамбль систем (т.е. все внешние условия одинаковы). Здесь производятся измерения для отдельных ансамблей, а потом происходит усреднение. Этот способ более предпочтителен.
Усреднение будем обозначать символами «< >». Отметим, что усреднение коммутативно с дифференциальными операторами.
Итак, усредняем:
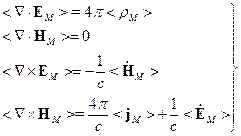
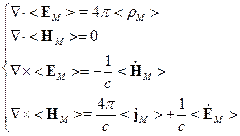
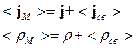
Среда под действием внешнего электромагнитного поля поляризуется, т.е. реагирует на внешнее воздействие. В случае, когда отсутствует пространственная дисперсия, поляризация характеризуется векторами электрической и магнитной поляризации 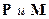 . Можно показать, что
. Можно показать, что 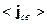 и
и 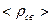 выражаются через
выражаются через 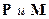 :
:
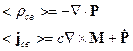
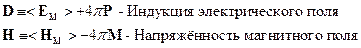
Введём обозначения: 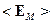
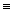
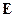 ;
; 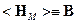
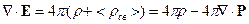
Перенесём второе слагаемое из правой части в левую и объединим его с 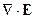 :
:
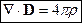
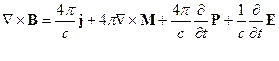
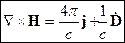
Итак, уравнения Максвелла для среды имеют вид:
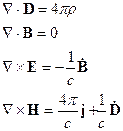
Запишем выражения для полей в среде:
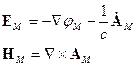
Усредним:
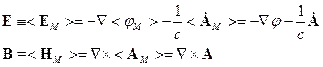
6 § 6. [Калибровка Лоренца в случае однородной изотропной среды]. Уравнение Даламбера (без учёта пространственной дисперсии)
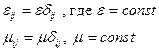
Калибровка Лоренца в случае вакуума:
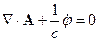
В случае однородной изотропной среды калибровка Лоренца примет вид:
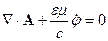
Запишем уравнения Максвелла:
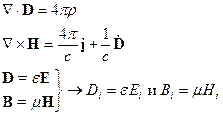
Здесь 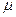 и
и 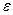 - числа, а векторы
- числа, а векторы 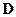 и
и 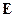 ,
, 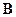 и
и 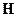 коллинеарные.
коллинеарные.
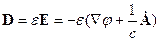
Для однородных изотропных сред имеем:
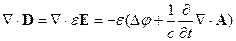
Используем калибровку Лоренца
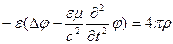
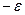 ð
ð 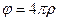
ð 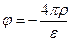
Мы получили уравнение Даламбера для скалярного потенциала электромагнитного поля в случае однородной изотропной среды.
ð 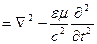
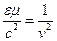 – скорость электромагнитных волн в среде
– скорость электромагнитных волн в среде
Запишем 4-ое уравнение Максвелла в среде без учёта пространственной дисперсии:
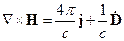
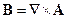 (6.1)
(6.1)
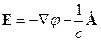 (6.2)
(6.2)
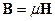 (6.3)
(6.3)
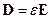 (6.4)
(6.4)
Так как среда однородна и изотропна, то
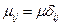 ,
,
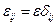 .
.
Из (6.1) и (6.3) следует:
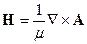
Из (6.2) и (6.44) следует:
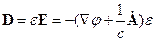
Используем то, что среда однородна и изотропна и запишем 4-е уравнение Максвелла:
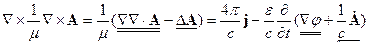
Сгруппируем элементы, подчёркнутые двумя линиями:
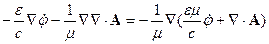
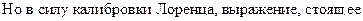 в скобках, даёт нуль.
в скобках, даёт нуль.
Теперь сгруппируем элементы, подчёркнутые одной линией. В результате получаем:
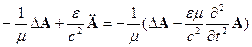
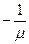 ð
ð 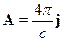
ð 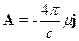
В итоге мы получили уравнение Даламбера для векторного потенциала электромагнитного поля в случае однородной изотропной среды.
7 § 7. Уравнения Максвелла для стационарного электромагнитного поля в среде. Уравнения Пуассона в электростатике
Поле стационарно, если оно не зависит явно от времени, т.е.
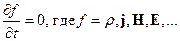
Уравнения Максвелла в этом случаем принимают вид:
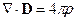 (7.1)
(7.1)
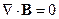 (7.2)
(7.2)
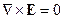 (7.3)
(7.3)
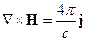 (7.4)
(7.4)
+ связи:
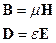
В электростатике используются (7.1) и (7.3) уравнения, а в магнитостатике (7.2) и (7.4).
Связь полей с потенциалами:
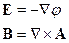
К электростатике относятся уравнения:
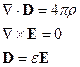
Причём второе уравнение автоматически удовлетворяет условию: 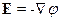
Выразим 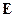 и
и 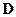 через потенциал:
через потенциал:
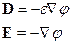
Распишем в компонентах:
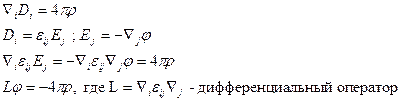
Мы получили уравнение Пуассона в электростатике.
1) Если среда неоднородная, тогда 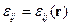 и мы не можем тензор
и мы не можем тензор 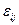 выносить за знак
выносить за знак 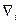 , тогда:
, тогда:
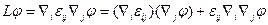
2) Если среда однородная, то 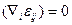 , т.е.
, т.е. 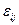 от координат не зависит и тогда:
от координат не зависит и тогда:
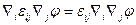
Если среда анизотропная, то в тензоре 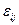 возникают несколько слагаемых:
возникают несколько слагаемых:
а) Однородная изотропная среда:
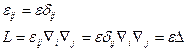
Тогда 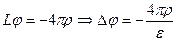
б) Однородная анизотропная среда:
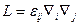
Функция Грина в случае неограниченной области.
Рассмотрим случай:
Влияние границы  отсутствует.
отсутствует.
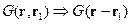 , т.е. мы можем помещать
, т.е. мы можем помещать 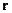 и
и 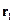 в любое место пространства.
в любое место пространства.
Получим Фурье-образ и саму функцию Грина. Рассмотрим случай вакуума.
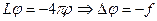
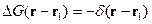
Для удобства, временно примем обозначение 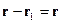 .
.
Тогда:
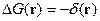

Запишем для 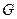 и
и 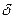 разложение в интеграл Фурье:
разложение в интеграл Фурье:
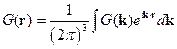
Здесь 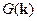 - фурье-образ, а
- фурье-образ, а 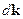 - элементарный объём в
- элементарный объём в 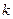 -пространстве.
-пространстве.
фурье-образ 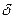 -функции равен
-функции равен 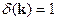
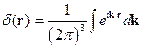
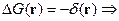
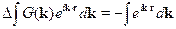
Рассмотрим левую часть этого равенства. Лапласиан 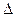 действует на
действует на 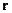 , значит, нам надо рассчитать
, значит, нам надо рассчитать 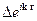
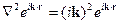
Т.е. 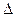 переходит в
переходит в 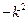 , тогда получим:
, тогда получим:
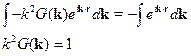
тогда 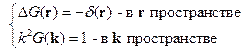
Переход в 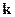 -пространство переводит дифференциальное уравнение в алгебраическое.
-пространство переводит дифференциальное уравнение в алгебраическое.
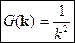
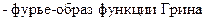
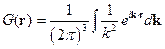
Этот интеграл можно взять, используя теорию вычетов. Получаем:
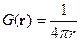
Производим обратную замену 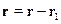 :
:
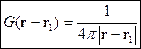
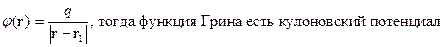
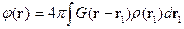
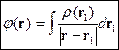
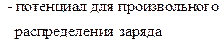
8 § 9. [Оператор трансляции]. Потенциал системы зарядов
Разложим функцию 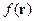 вблизи точки
вблизи точки 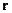 :
:
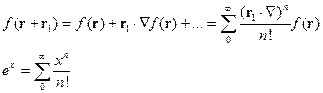
Теперь, если 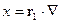 , тогда:
, тогда:
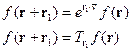
Оператор 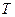 действуя на
действуя на 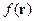 переводит её в
переводит её в 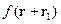
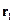
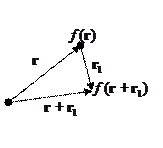 - вектор трансляции.
- вектор трансляции.
Тогда оператор трансляции 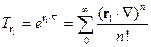
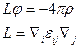
Частное решение уравнения Пуассона:
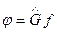
Здесь 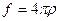 , а
, а 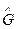 есть интегральный оператор, ядро которого есть функция Грина.
есть интегральный оператор, ядро которого есть функция Грина.
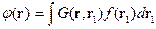
В точке 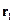 источник, а
источник, а 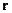 - точка наблюдения, где мы считаем потенциал.
- точка наблюдения, где мы считаем потенциал.
Для неограниченных областей имеем:
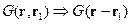
Т.е. пространство становится однородным, так как нет границ и начало отсчёта можно выбрать где угодно.
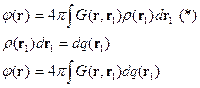
Формула (*) позволяет рассчитать потенциал по заданному распределению заряда. Затем посчитать напряжённость 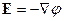 .
.
Теперь рассмотрим систему из 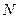 точечных зарядов:
точечных зарядов:
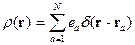
Здесь 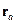 - точки, где расположены заряды.
- точки, где расположены заряды.
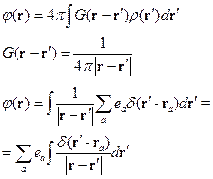
Но по определению 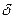 -функции:
-функции:
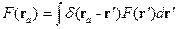
Окончательно имеем:
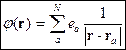
9 § 10. Электрические (дипольный [и квадрупольный]) моменты системы зарядов. [Магнитный дипольный момент системы токов.]
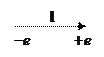
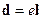
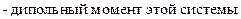
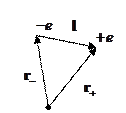
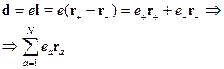
Таким образом, мы обобщили дипольный момент на систему из 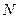 точечных зарядов.
точечных зарядов.
Перейдём от точечных зарядов к 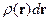 :
:
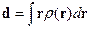
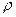 задаёт распределение зарядов.
задаёт распределение зарядов. 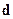 - дипольный момент системы зарядов, он характеризует распределение зарядов в пространстве.
- дипольный момент системы зарядов, он характеризует распределение зарядов в пространстве.
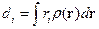
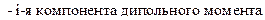
Тензор квадрупольных моментов 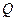 - тензор второго ранга.
- тензор второго ранга.
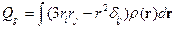
Сумма диагональных элементов 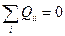 , покажем это:
, покажем это:
Рассмотрим 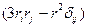 :
:
Пусть 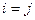 , тогда (по повторяющимся индексам подразумевается суммирование):
, тогда (по повторяющимся индексам подразумевается суммирование): 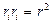 ,
, 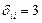
И мы получаем, что 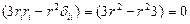 или
или 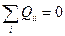
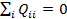
Покажем, что сферически-симметричный заряд имеет тензор 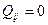 :
:
Так как заряд сферически симметричен, то 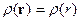 , т.е.
, т.е. 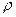 зависит только от
зависит только от 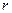 , но тогда
, но тогда 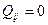 .
.
Для магнитного дипольного момента системы токов:

По замкнутому контуру 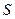 течёт ток
течёт ток 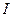
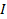 . Магнитный момент
. Магнитный момент 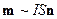 . Коэффициент пропорциональности в этом выражении в Гауссовой системе единиц равен
. Коэффициент пропорциональности в этом выражении в Гауссовой системе единиц равен 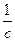 :
:
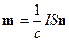
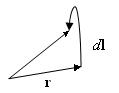 Рассмотрим частный случай:
Рассмотрим частный случай:
В этом случае возникает площадка 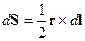 .
.
Пусть 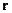 - радиус-вектор точечного заряда,
- радиус-вектор точечного заряда, 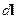 - траектория его движения, тогда:
- траектория его движения, тогда:
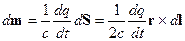
Пусть рассматриваемый заряд имеет величину 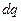 , тогда
, тогда 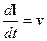 - скорость заряда
- скорость заряда 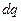 движущегося по траектории
движущегося по траектории 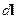 , тогда:
, тогда:
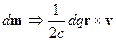
Эта формула позволяет провести обобщение на систему зарядов, тогда:
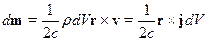
Это формула для элементарного магнитного момента. Значит, магнитный момент некоторой системы токов будет:
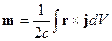
Если есть система движущихся точечных зарядов, то: