Задачи по курсу «Физические основы фотоники» (минимум)
1. (Г.3) Вычислить градиент функции 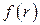 , зависящей только от модуля радиус-вектора , зависящей только от модуля радиус-вектора 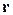 . . | |
2. (Г.5) Вычислить, 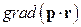 , , 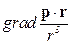 , , 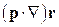 , , 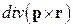 , , 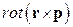 , где , где 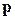 – постоянный вектор. – постоянный вектор. | |
3. (Г.8) Пользуясь теоремой Остроградского-Гаусса, вычислить интегралы: 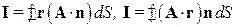 если объем, который охватывает замкнутая поверхность, равен если объем, который охватывает замкнутая поверхность, равен 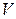 ; ; 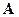 – постоянный вектор. – постоянный вектор. | |
4. (Г.12) Определить напряженность электрического поля внутри и снаружи равномерно заряженного шара. Объемная плотность заряда равна 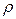 , радиус шара , радиус шара 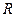 . . | |
5. (Г.13) В равномерно заряженном шаре с объемной плотностью заряда 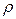 имеется шарообразная полость, центр которой расположен на расстоянии имеется шарообразная полость, центр которой расположен на расстоянии 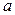 от центра шара. Найти напряженность электрического поля внутри полости, внутри шара и снаружи шара. Радиусы шара и полости равны соответственно от центра шара. Найти напряженность электрического поля внутри полости, внутри шара и снаружи шара. Радиусы шара и полости равны соответственно 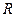 и и 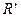 . . | |
6. (А.190')Внутри бесконечного цилиндра радиуса 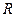 параллельно его оси течет однородный ток с объемной плотностью параллельно его оси течет однородный ток с объемной плотностью 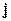 . Пользуясь интегральной формой уравнения Максвелла . Пользуясь интегральной формой уравнения Максвелла 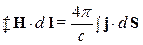 , найти напряженность , найти напряженность 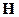 магнитного поля внутри и снаружи цилиндра. магнитного поля внутри и снаружи цилиндра. | |
7. (Г.65) Найти напряженность магнитного поля внутри цилиндрической полости цилиндрического проводника, по которому течет ток, равномерно распределенный по его сечению с плотностью 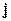 . Оси цилиндра, образующего полость, и цилиндрического проводника, параллельны и находятся друг от друга на расстоянии . Оси цилиндра, образующего полость, и цилиндрического проводника, параллельны и находятся друг от друга на расстоянии 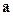 . . | |
8. (Г.81) Показать, что постоянное однородное магнитное поле 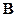 можно описывать векторным потенциалом можно описывать векторным потенциалом 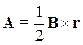 . . | |
9. (Г.140) Найти интенсивность излучения частицы массы 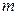 , движущейся по круговой орбите радиуса , движущейся по круговой орбите радиуса 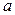 , под действием кулоновских сил. Выразить ответ через энергию частицы. , под действием кулоновских сил. Выразить ответ через энергию частицы. | |
10. (А.292) Простейшая линейная антенна представляет собой тонкий прямолинейный провод длины l, по которому течет ток 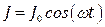 . Определить интенсивность I длинноволнового излучения антенны в среднем за период колебания тока. . Определить интенсивность I длинноволнового излучения антенны в среднем за период колебания тока. | |
11. (А.19) Напряженность электрического поля в пространстве известна: 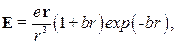 где где 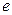 и и 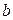 – положительные постоянные, а – положительные постоянные, а 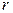 – расстояние до начала координат. Определить распределение объемной плотности – расстояние до начала координат. Определить распределение объемной плотности 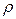 заряда, создавшего это поле. Чему равен полный заряд заряда, создавшего это поле. Чему равен полный заряд 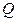 ? ? | |
12. (Г.10)Показать, что дивергенция вектора 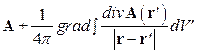 равна нулю. равна нулю. | |
| 13.Теорема Остроградского-Гаусса. Теорема Стокса. | |
Вопросы по курсу «Физические основы фотоники»
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
1. Плотность заряда и её вид в случае системы точечных зарядов. Уравнения Максвелла для электромагнитного поля в вакууме.
2. Закон сохранения заряда [в форме уравнения непрерывности]. Теорема Остроградского-Гаусса.
3. Потенциалы электромагнитного поля в вакууме. Градиентная инвариантность.
4. Типы калибровок.
5. [Микро- и макро-] уравнения Максвелла для электромагнитного поля в среде. Потенциалы электромагнитного поля в среде.
6. [Калибровка Лоренца в случае однородной изотропной среды.] Уравнение Даламбера (без учёта пространственной дисперсии).
7. Уравнения Максвелла для стационарного электромагнитного поля в среде. Уравнения Пуассона в электростатике.
8. Функция Грина в случае неограниченной области.
9. [Оператор трансляции.] Потенциал системы зарядов.
10. Электрические (дипольный [и квадрупольный]) моменты системы зарядов. [Магнитный дипольный момент системы токов.]
11. Электрическое поле системы зарядов на больших расстояниях.
12. Система зарядов во внешнем электростатическом поле.
13. Векторный потенциал системы стационарных токов. Приближение линейного тока.
14. Уравнения Максвелла для квазистационарного электромагнитного поля. [Условие квазистационарности поля.]
15. Уравнения Максвелла электромагнитных волн в вакууме. Волновое уравнение в случае вакуума.
16. Плоская монохроматическая волна. Уравнения Максвелла в случае плоской монохроматической волны в вакууме. [Разложение электромагнитных полей по плоским монохроматическим волнам.]
17. Функция Грина уравнения Гельмгольца.
18. Запаздывающая функция Грина уравнения Даламбера.
19. Запаздывающие потенциалы. [Разложение запаздывающих потенциалов в ряды по малому параметру.]
20. Дипольное излучение.
21. Волновая зона дипольного излучения.
22. Интенсивность дипольного излучения в волновой зоне. Примеры.
Вопросы по курсу «Физические основы фотоники» (минимум)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
1. Плотность заряда и её вид в случае системы точечных зарядов. Уравнения Максвелла для электромагнитного поля в вакууме.
2. Закон сохранения заряда [в форме уравнения непрерывности. Теорема Остроградского-Гаусса.]
3. Потенциалы электромагнитного поля в вакууме. Градиентная инвариантность.
4. Типы калибровок.
5. [Микро- и макро-] уравнения Максвелла для электромагнитного поля в среде. Потенциалы электромагнитного поля в среде.
6. Уравнения Максвелла для стационарного электромагнитного поля в среде. Уравнения Пуассона в электростатике.
7. Электрические (дипольный [и квадрупольный]) моменты системы зарядов. [Магнитный дипольный момент системы токов.]
8. Уравнения Максвелла для квазистационарного электромагнитного поля. [Условия квазистационарности поля]
9. Уравнения Максвелла электромагнитных волн в вакууме. Волновое уравнение в случае вакуума.
10. Плоская монохроматическая волна. Уравнения Максвелла в случае плоской монохроматической волны в вакууме. Разложение электромагнитных полей по плоским монохроматическим волнам.
11. Запаздывающие потенциалы. Разложение запаздывающих потенциалов в ряды по малому параметру.
12. Дипольное излучение. Волновая зона дипольного излучения.
Список литературы
Основная литература
1. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика:
a. Т.2. Теория поля. М, Наука, 2012. 530.1 (075.8) Л-222
b. Т.8. Электродинамика сплошных сред. М, Наука, 2005. 538.3 (075.8) Л-222
2. Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. М., Наука, 1990, 1979. 537.8 (075.8) В-493; 538.56 (075.8) В-493
3. Бредов М.М., Румянцев В.В., Топтыгин И.Н.Классическая электродинамика. М., Наука, 1985. 530.1 (075.8) Б-877
4. Галицкий В.М., Ермаченко В.М. Макроскопическая электродинамика. М., Высшая школа, 1988. 537.8 (075.8) Г-158
5. Алексеев А.И. Сборник задач по электродинамике, М., Наука, 1977.
Дополнительная литература
1. Батыгин В.В., Топтыгин И.Н. Сборник задач по электродинамике. М, Наука, 1970 г. 538.3 (076.1) Б-288
2. Сиротин Ю.И., Шаскольская М.П. Основы кристаллофизики. М., Наука, 1979
3. Гинзбург В.Л. Теоретическая физика и астрофизика. Дополнительные главы. М., Наука, 1987
Литература к задачам
1. Гречко Л.Г., «Сборник задач по теоретической физике», Издательство «Высшая школа» Москва – 1972
(Г.№)
2. Алексеев А.И., «Сборник задач по электродинамике», М., Наука, 1977
(А.№)
3. Батыгин В.В., Топтыгин И.Н., «Сборник задач по электродинамике», М., Наука, 1970
538.3 (076.1) Б-288
(Б.№)
4. Джексон Дж., «Классическая электродинамика», М., Мир, 1965
