Приближенные развертки развертывающихся поверхностей

Построение приближенных разверток выполняется в следующей последовательности:

1) заданную развертывающуюся линейчатую поверхность заменяют (аппроксимируют) гранной поверхностью;

2)строят точную развертку гранной поверхности;

3)точную развертку принимают за приближенную развертку заданной поверхности.

Для некоторых линейчатых развертывающихся поверхностей нет необходимости в их замене гранными поверхностями. Так, например, отсек цилиндрической поверхности вращения радиуса r и высотой h имеет разверткой прямоугольник со сторонами h и 2pr (рис. 13.5).

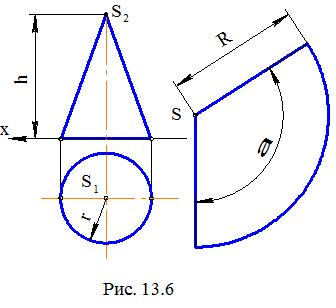
Разверткой конической поверхности вращения высотой h и основанием радиуса r является сектор радиуса R = 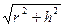c углом a = 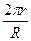(рис. 13.6). Рассмотрим пример построения приближенных разверток.

Задача. Дан отсек конической поверхности (рис. 13.7). Построить его приближенную развертку.

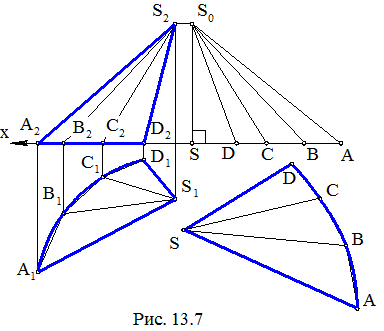Плоскую кривую линию – направляющую конической поверхности вначале заменяют вписанной ломаной линией ABCD(A₁B₁C₁D₁, A₂B₂C₂D₂), которая по условию задачи принадлежит плоскости проекций П₁ и поэтому A₁B₁C₁D₁ – ее НВ. Затем соединяют вершины ломаной с вершиной S конической поверхности и получают вписанную пирамидальную поверхность SABCD, которой заменяют данную коническую поверхность. Используя метод прямоугольного треугольника, строят диаграмму НВ ребер вписанной пирамидальной поверхности. При этом SS₀ – общая разность высот концов ребер пирамиды; SD = S₁D₁, SC = S₁C₁, SB = S₁B₁, SA =

= S₁A₁; S₀D, S₀C, S₀B, S₀A – представляют собой НВ ребер пирамиды. SDCBA – развертка боковой поверхности заданного конического отсека.

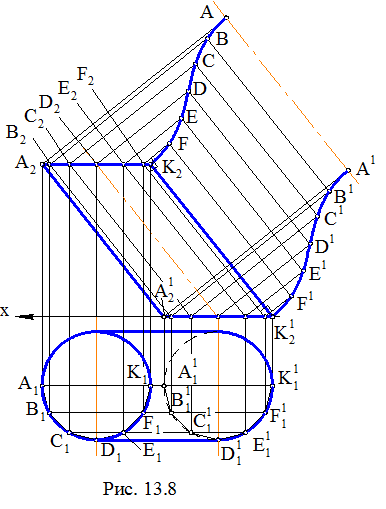
Задача. Дан отсек поверхности эллиптического цилиндра (рис. 13.8). Построить развертку ее боковой поверхности.

Впишем в данную поверхность некоторую призматическую поверхность, разделив направляющую линию цилиндра – окружность, на равное число частей, например на 12 (на рисунке, в силу симметричности заданной поверхности, для простоты построений выполнено деление половины поверхности на 6 частей). Боковые ребра вписанной призмы являются фронталями, а ее основания – многоугольники принадлежат горизонтальным плоскостям уровня. По этой причине боковые ребра проецируются на П₂ в НВ, а многоугольники оснований – в НВ на П₁.

Отмеченные условия задачи соответствуют методу раскатки для построения развертки вписанной призмы. Поскольку призма имеет плоскость симметрии, проходящую через линию центров образующих эллиптический цилиндр окружностей и являющуюся фронтальной плоскостью уровня, то для сокращения построений выполним построения развертки только половины призмы. Вращение призмы по методу раскатки следует начинать с ребра КК¹ (К₁К₁¹, К₂К₂¹). Поэтому плоскостью развертки призмы будет фронтальная плоскость уровня, проходящая через ребро КК¹. Последовательным вращением вокруг ребер призмы добиваемся совмещения всех ее граней с плоскостью развертки. При этом К₂F = K₂¹F¹ = = K₁¹F₁¹ = K₁F₁; FE = F¹E¹ = F₁¹E₁¹ = F₁E₁ и т. д. Полученный многоугольник ABCD… D¹C¹B¹A¹ представляет собой точную развертку половины боковой поверхности вписанной призмы, которая в свою очередь определяет приближенную развертку соответствующей половины поверхности эллиптического цилиндра.

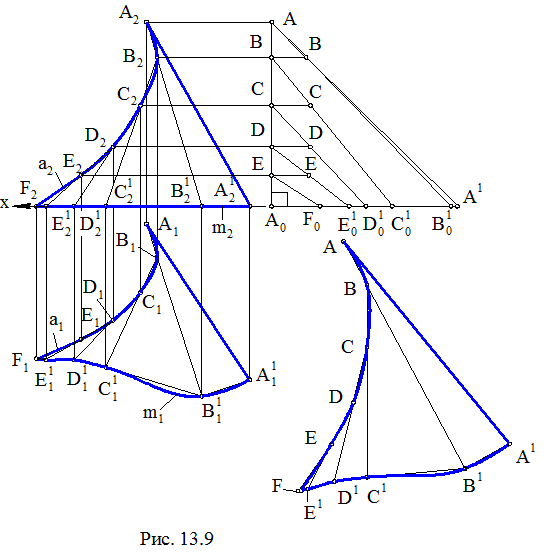Задача. Дан отсек торсовой поверхности (рис. 13.9). Построить его развертку.

Торсовая поверхность – это линейчатая развертывающаяся поверхность, образованная касательными прямыми к пространственной кривой, которая имеет название ребра возврата этой поверхности. В нашей задаче отсек заданной поверхности ограничен ребром возврата а (а₁, а₂), плоской кривой m (m₁, m₂) и отрезком АА¹ ее образующей. Заменим кривую m вписанной ломаной линией A¹B¹C¹D¹E¹F с проекциями A₁¹B₁¹C₁¹D₁¹E₁¹F₁ и A₂¹B₂¹C₂¹D₂¹E₂¹F₂. Затем поступим следующим образом:

1) соединим точки А и В¹ для получения отрезка АВ¹(А₁В₁¹, А₂В₂¹);

2) отметив точку пересечения АВ¹ ∩ а = В(В₁, В₂), соединим точки В и С¹ для получения отрезка ВС¹(В₁С₁¹, В₂С₂¹);

3) отметив точку пересечения ВС¹ ∩ а = С(С₁, С₂), соединим точки С и D¹ для получения отрезка СD¹(С₁D₁¹, C₂D₂¹);

4) отметив точку пересечения СD¹ ∩ а = D(D₁, D₂), соединим точки D и Е¹ для получения отрезка DЕ¹(D₁Е₁¹, D₂Е₂¹);

5) отметив точку пересечения DЕ¹ ∩ а = Е(Е₁, Е₂), соединим точки Е и F₁ для получения отрезка EF(E₁F₁, E₂F₂).

В итоге выполнения построений получим вписанный в ребро возврата а пространственный многоугольник ABCDEF(A₁B₁C₁D₁E₁F₁, A₂B₂C₂D₂E₂F₂) и вписанную в торсовую поверхность гранную поверхность с ребрами АА¹, АВ¹, ВС¹, СD¹, DE¹, EF.

Очевидно, гранями вписанной в торсовую поверхность гранной поверхности являются треугольники, у которых две вершины являются вершинами плоской ломаной линии, вписанной в линию m, а третья вершина – это вершина пространственной ломаной, вписанной в ребро возврата а. Сторона одного из двух соседних треугольников принадлежит стороне другого и служит ребром гранной поверхности. Дальнейшие построения заключаются в определении НВ двух из трех сторон каждого треугольника методом прямоугольного треугольника, поскольку третья сторона спроецирована на П₁ в НВ. Для этого строится диаграмма НВ сторон треугольников – граней. При этом на прямой АА₀ от точки А₀ откладываются разности высот концов отрезков – сторон треугольников, а по оси х от точки А₀ – длины горизонтальных проекций этих сторон. Причем А₀F₀ = E₁F₁, А₀E₀¹ =

= D₁E₁¹, А₀D₀¹ = C₁D₁¹, А₀C₀¹ = B₁C₁¹, А₀В₀¹ = А₁В₁¹, А₀A¹ = А₁A₁¹.Затем выполняются последовательные построения треугольников – граней по трем их сторонам, приводящие к плоской области, ограниченной линией ABCD…D¹C¹B¹A¹. Эта плоская область будет приближенной разверткой заданной торсовой поверхности.