Пример решения задания №4

Задание № 4

КРУЧЕНИЕ. РАСЧЕТ ВАЛА НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ

Определить диаметры ступенчатого вала из условия прочности и жесткости на кручение.

1. Вычертить схему с указанием числовых данных.

2. Составить уравнения внутренних крутящих моментов по участкам ( Т_кр )

3. Построить эпюру внутренних крутящих моментов.

4. Из условия прочности определить диаметр вала на каждом участке. Полученный результат округлить (ГОСТ 6636-69) до ближайшего значения из ряда R40: I0; 10,5; II; II,5; I2; I3; I4; I5; I6; 17; I8; I9; 20; 2I; 22; 24; 25; 26; 28; 30; 32; 34; 36; 38; 40; 42; 45; 48; 50; 52; 55; 60; 63; 65; 70; 75; 80; 85; 90; IOO; I05; IIO; I20; I25; I30; I40; I50; I60 мм.

5. Приняв допускаемый относительный угол закручивания (на 1 погонный м) [q]= I,75×10^-2 рад/м и модуль сдвига G = 8×I0¹⁰ Па, из условия жесткости определить диаметр вала по участкам. Полученный результат округлить до ближайшего значения из ряда R40.

6. Окончательно принять диаметр вала на каждом участке по наибольшему значению, полученному из условий прочности и жесткости.

7. Определить угол закручивания по длине вала. Определить взаимный угол закручивания концевых сечений. Схема вала приведена на рис.4.1. Данные для расчета взять в табл. 4.1.

Таблица 4.1

Вариант	l, м	Т1, Н×м	Т2, Н×м	Т3, Н×м	[t], МПа
	0,8
	1,0
	1,2
	0,6
	0,9
	1,4
	1,6
	1,8
	2,0
	0,7

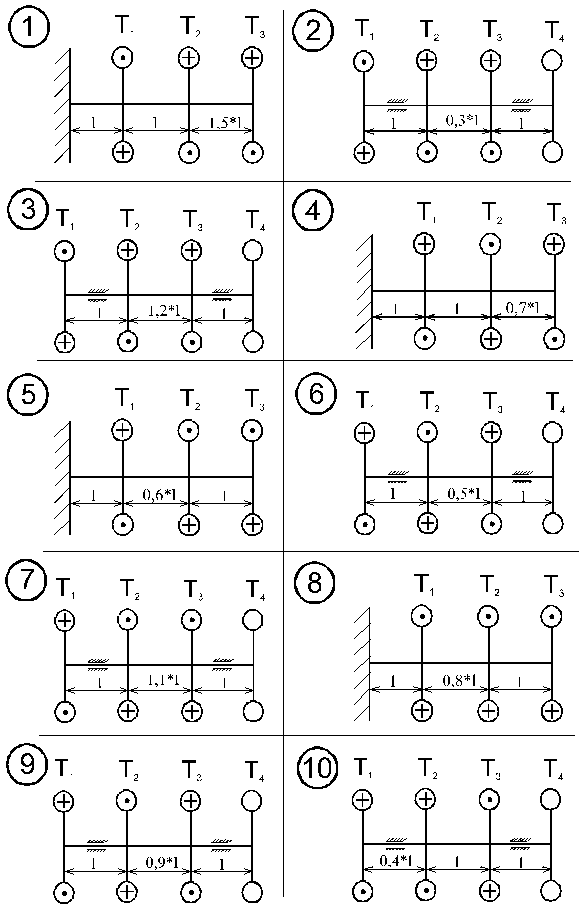
Рис.4.1

Пример решения задания №4

Задание.

Брус круглого поперечного сечения нагружен, как показано на рис. 4,2. Из услови прочности и жесткости определить диаметры поперечных сечений ступенчатого бруса при условии, что Т₁ = 300 Н*м; Т₂ = 500 Н*м; Т₃ = 100 Н*м; = I,75×10^-2 рад/м; [t] = 45 Мпа; G = 8×I0¹⁰ Па.

Решение.

Не следует смешивать понятия момента на шкиве и крутящего момента в сечении. Под крутящим моментом в сечении следует подразумевать внутренний силовой фактор. Момент на шкиве, являющийся внешним воздействием, будем, в отличие от внутреннего, называть скручивающим.

Для определения знака крутящего момента примем следующее правило: если смотреть на отсеченную часть бруса со стороны внешней нормали к сечению, то момент сечении будет положителен в том случае, когда сумма внешних скручивавших моментов поворачивает отсеченную часть бруса по часовой стрелке, и отрицателен при повороте части бруса в противоположном направлении.

Неизвестный скручивающий момент Т₄ найдем из уравнения равновесия для всего бруса. Условно примем направление момента Т₄ совпадающим с направлением момента Т₂, которое принято за положительное. Тогда уравнение равновесия принимает вид

– Т₁ + Т₂ –Т₃ + Т₄ = 0

Из решения этого уравнения получим

Т₄ = Т₁ – Т₂ +Т₃ = 300 – 500 + 100 = –100 Н*м.

Знак минус означает, что первоначальное направление скручивающего момента Т₄ выбрано неверно.

После того, как стали известны все скручивающие моменты эпюру крутящих моментов можно строить начиная как с правого так и с левого конца бруса. За начало координат примем левый конец бруса.

Для построения эпюры крутящих моментов применяем метод сечений к каждому участку вала в отдельности (следует заметить, что построение эпюры крутящих моментов совершенно аналогично построению эпюры продольных сил). Крутящие моменты в сечениях определяются как алгебраические суммы внешних моментов, приложенных по одну сторону (в нашем случае по левую) от сечения.

Определим крутящие моменты на каждом участке, проведя последовательно сечения на трехучастках бруса и рассмотрим равновесие соответствующих оставшихся левых частей.

Т₁ Т₂ Т₃ Т₄

1 2 3

А B C D

1 2 3

0.5*ll l

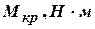
-300 0,026

0,007

0

0,009

Рис.4.2

В сечении 1-1

.

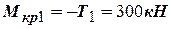В сечении 2-2

.

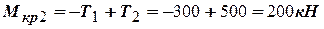В сечении 3-3

По полученным данным строим эпюру крутящих моментов, откладывая по вертикальной оси значения моментов. Положительные моменты откладываем вверх по осевой линии, отрицательные - вниз (см. рис. 4.2).

По найденным значениям крутящих моментов из расчетов на прочность и жесткость в каждом сечении определим диаметры валов.

Расчет на прочность ведется по допускаемому напряжению при кручении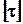

(4.1)

где 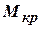–крутящий момент, действующий в сечении бруса;

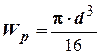–полярный момент сопротивления для круглого сечения, 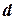–диаметр вала.

Из формулы (4.1) выразим диаметр

(4.2)

По формуле (4.2) определим диаметры для всех сечений.

Сечение 1-1

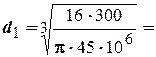0,0324м.

Сечение 2-2

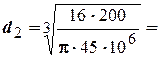0,0283м.

Сечение 3-3

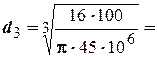0,0225м.

Расчет на жесткость ведется по допускаемому относительному углу закручиванию

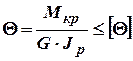(4.3)

где 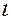–длина участка; 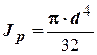–полярный момент сопротивления круглого сечения.

Условие (4.3) часто выдвигается на первое место при длинных валах.

В соответствии с формулой (4.3) определим диаметр вала из условия жесткости

(4.4)

По формуле (4.4) определим диаметры для всех участков.

Сечение 1-1

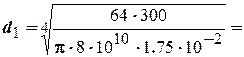0,0457м.

Сечение 2-2

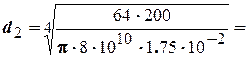0,0413м.

Сечение 3-3

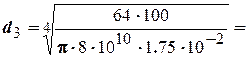0,0347м.

В соответствии с расчетами на прочность и жесткость выбираем наибольшее значение диаметров для каждого учаска и полученный результат округляем до ближайшего значение из ряда по ГОСТ 6636-69. В результате получим следующие значения: .

Абсолютные углы закручивания для каждого участка можно определить по формуле

(4.5)

Полярные моменты инерции для каждого сечения

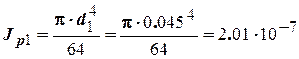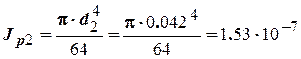м⁴;

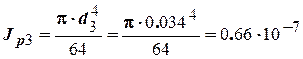м⁴;

м⁴.

Далее определим углы закручивания.

Первый участок

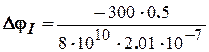= – 0,009 рад – угол поворота сечения В относительно сечения А (или угол закручивания участка АВ).

Второй участок

= 0,016 рад – угол поворота сечения С относительно сечения В (или угол закручивания участка ВС).

Третий участок

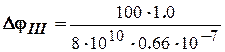= 0,19 рад –угол поворота сечения D относительно сечения C (или угол закручивания участка CD).

Строим эпюру углов закручивания для всего вала. За начало координат выбран крайний левый конец бруса (сечение А). В пределах каждого из участков бруса эпюра линейна, поэтому достаточно знать углы поворота только для граничных сечений участков.

В сечении В полный угол закручивания вала относительно сечение А равен 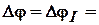– 0,009рад;

В сечении C полный угол закручивания вала относительно сечение А равен

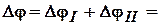– 0,009+0,016 = 0,007рад;

В сечении D полный угол закручивания вала относительно сечение А равен

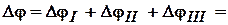– 0,009+0,016 +0,019= 0,026рад;

Эпюра полных углов закручивания ступенчатого вала показана на рис.4.2. Ординаты этой эпюры дают значения углов поворота соответствующих поперечных сечений бруса.