Пример решения задания №5

Задание № 5

РАСЧЕТ ДВУХОПОРНОЙ БАЛКИ НА ПРОЧНОСТЬ

ПРИ ПЛОСКОМ ИЗГИБЕ

Построить эпюры поперечных сил и изгибающих моментов и подобрать прямоугольное сечение стальной балки. Схема нагружения балки показана на рис. 5.1, данные приведены в таблице 5.1.

Таблица 5.1

Вариант	Расстояния (l, м)	q, кН/м	Р, кН	М, кН×м	h / b
a	b	c	l
	0,6	0,5	2,0					1:1
	0,7	0,6	1,8	9,5				2:1
	0,8	0,7	1,6	9,0				3:1
	0,9	0,8	1,5	8,5				3:2
	1,0	0,9	1,4	8,0				4:1
	1,1	1,0	1,2	7,5				5:2
	1,2	1,1	1,0	7,0				2:1
	1,3	1,2	0,8	6,5				3:1
	1,4	1,3	0,6	6,0				1:1
	1,5	1,4	0,4	5,5				3:2

Содержание и порядок расчета

1. Вычертить в масштабе заданную схему балки с указанием размеров и величин нагрузок.

2. Определить опорные реакции и выполнить проверку правильности их определения.

3. Построить эпюры поперечных сил и изгибающих моментов с обязательным составлением уравнений для Q_Z,и M_Z для каждого участка.

4. Определить положение наиболее нагруженных сечений балки и отметить их на схеме.

5. Подобрать прямоугольное сечение из условия прочности [s]_и=160МПа и заданном соотношении размеров сечения: h / b, где h – высота сечения, b – ширина.

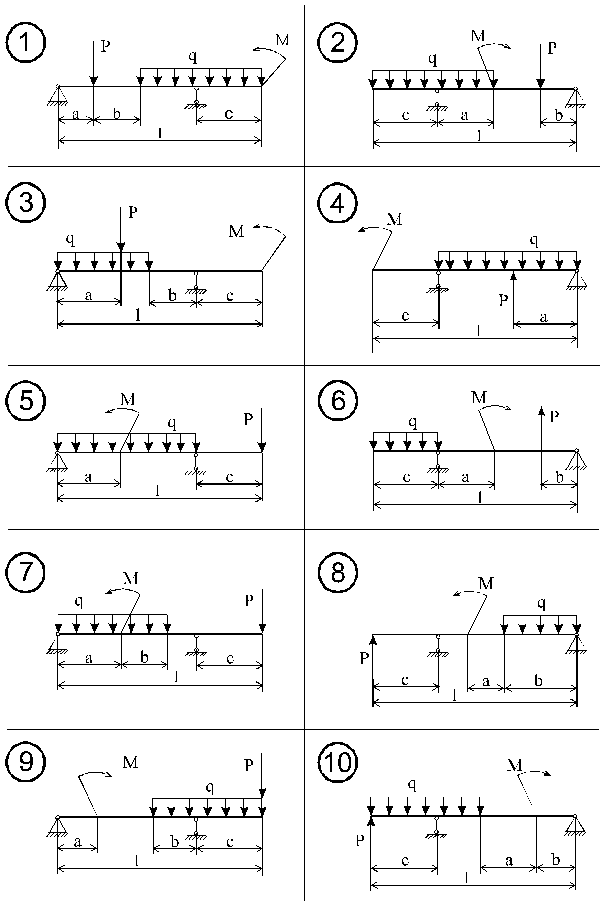Рис. 5.1

Указания к заданию № 5

При построении эпюр поперечных сил и изгибающих моментов необходимо соблюдать правило знаков. Знаки для и связаны с характером деформации балки при действии внешних сил (рис. 5.2, 5.3)

М_Z>0 Q_z>0 Q_Z<0

m m

M_Z<0

n n

Q_Z>0 Q_z<0

Рис.5.2 Рис.5.3

Изгибающий момент в сечении положителен, если балка в этом сечении изгибается выпуклостью вниз, - отрицателен, если балка изгибается выпуклостью вверх (рис.5.2).

Поперечную силу будем считать положительной, если она стремится сдвинуть левое сечение балки вверх относительно правого или правое сечение вниз относительно левого (рис. 5.3) и отрицательной, если она стремится сдвинуть левое сечение балки относительно правого вниз или правое сечение вверх относительно левого (рис. 5.3).

Поперечная сила в данном сечении определяется как алгебраическая сумма сил, расположенных только по одну сторону от рассматриваемого сечения, а изгибающий момент в данном сечении равен алгебраической сумме моментов сил, расположенных только с одной стороны относительно центра тяжести этого сечения. (Следует заметить, что построение эпюр изгибающих моментов и поперечных сил совершенно аналогично построению эпюры продольных сил (зад.3) и эпюры крутящих моментов (зад.4)).

Пример решения задания №5

Задание. Построить эпюры и .Подобрать стальную прямоугольную балку (h/b=2), нагруженную, как показано на рис. 5.4.

Дано: кН ; М = 40кН*мм ; q = 20кН/м ; 160Мпа ; 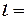2м.

P R_A R_B

q

M

A B

Z₁

Z₂ Z₃

l l l

10

Q_Z (kH)

-20

-30

22,5

20

M_Z (kH*м)

1,5м

-40

Рис.5.4

Решение. Для вычисления и необходимо определить реакции опор. Для этого запишем уравнения равновесия.

Сумма моментов вех сил относительно шарнира А равна 0

,

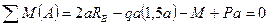30кН.

Сумма моментов вех сил относительно шарнира В равна 0

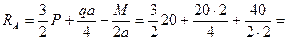30кН.

Для проверки используем третье уравнение равновесия: сумма проекций всех сил на вертикальную ось Y равна 0:

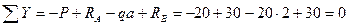
0 = 0

Тождество выполнено, значит реакции найдены верно.

Запишем уравнения для поперечной силы и изгибающего момента на 1-м участке м;

кН (постоянная на всем участке);

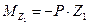(линейная зависимость).

Для построения эпюры 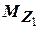найдем значение для двух точек:

при ;

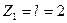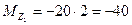при м кН*м.

Построение эпюр и 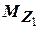показано на рис. 5.4.

Поперечные силы и изгибающие моменты на 2-м участк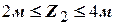е

10кН; (постоянная на всем участке);

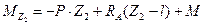(линейная зависимость).

Для построения эпюры на втором участке находим:

при 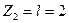м кН*м;

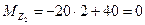при м кН*м .

Поперечные силы и изгибание моменты на 3-м участке. Для этого сечения удобно рассмотреть правую часть 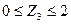м.

(линейная зависимость).

Для построения эпюры 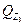находим значение 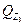для двух крайних точек

при 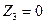м кН;

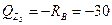при м кН.

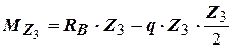(параболическая зависимость).

Для построения эпюры изгибающих моментов найдем значения моментов в трех точках (две крайние точки и точка, соответствующая экстремуму функции ):

при ;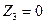

при м кН*м.

Найдем координату, где 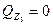(т.е. функция имеет экстремум – максимум):

,

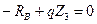откуда 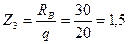м.

Тогда 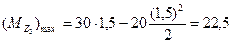кН*м.

При м кНм.

По наиболее опасному сечению (сечение на опоре А ), где действует наибольший изгибающий момент =40кН*м, подберем сечение балки согласно условию задачи из услови прочности сечения по нормальным напряжениям

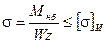(5.1)

где 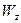–момент сопротивления сечения, который для прямоугольного сечения можно определить как

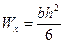(5.2)

Учитывая заданное условие h/b=2, получим м³.

Подставляя (5.2) в (5.1) получим 0,072м

h=2*0,072=0,144м.

Размеры представлять в мм.