I. Некоторые сведения о приближенных вычислениях

Методические указания

для самостоятельной работы студентов

при изучении дисциплины

«Основы информационных технологий и программирование»

(численные методы в инженерных расчетах)

специальностей:

6.090509 - «Судовые енергетические установки и

оборудование»;

6.092203 - «Електромеханические системы автоматизации и

електропривод»;

6.092301 - «Технология и оборудование сварочного

производства»;

6.090210 - «Двигатели внутреннего сгорания».

6.100201 - «Корабли и океанотехника».

Херсон 2012

Тендитный Ю.Г., Тендитная Н.В. Избранные вопросы вычислительной математики. Конспект лекций по разделу " Численные методы ".

Херсон, филиал НУК, 2012.

-36с.

Конспект лекций (сокращенный, переработанный) предназначен для студентов высших учебных технических заведений, которые изучают курс " Вычислительная техника и программирование". В конспекте изложены теоретические сведения по вопросам вычислительной математики, изучение которых предусмотрено программой названного курса. По теме " Решение нелинейных уравнений " приведены программы для компьютера, написанные на языке FORTRAN.

Спис. лит. - 6 назв.

Рецензент к.т..н. . доц. О.Н. Дудченко

СОДЕРЖАНИЕ

Предисловие …………………………………………………………………….. 3

I. Некоторые сведения о приближенных вычислениях …………………….. 4

2. Решение нелинейных уравнений …………………………………………. 8

З. Решение систем линейных уравнений …………………………………… 19

4. Интерполирование зависимостей …………………………………………. 19

5. Приближенное интегрирование функций ………………..………………. 20

5.2. Вычисление методом трапеций .…………………………………….…… 21

5.3. Вычисление методом Симпсона …………………………………….…… 21

Приложения (порядок выполнения работ на ПК )……………………….. 26

Таблицы с исходными уравнениями …………………………………………. 32

Литература …………………………………………………………………….... 35

Предисловие

Современное развитие науки и техники тесно связанно с использо­ванием ЭВМ, ставших рабочим инструментом инженера, конструк­тора, ученого. Компьютеры используются для изучения реальных сложных объектов, систем, процессов и явлений, при создании систем управления этими объ­ектами и процессами. И здесь на первый план выступает их математичес­кая модель, т. е. описание объектов, явлений и процессов на математиче­ском языке - с помощью функций, уравнений (трансцендентных и алгебраи­ческих, дифференциальных, интегральных и т,д.), неравенств, логических отношений. Для таких задач разработаны алгоритмы и методы решения, су­ществует ряд программ для их решения на ЭВМ. Однако постоянное разви­тие вычислительной техники и применение новых языков программирования в инженерной практике требует совершенствования имеющихся и создания новых программ. Особенно актуальна данная задача для пользователей пе­рсональных ЭВМ, так как для ПЭВМ в отечественной практике недостаточно разработано программное обеспечение.

В данном пособии приведены алгоритмы и тексты программ, написан­ные на наиболее употребляемых в инженерной практике языке программи­рования - FORTRAN. Стиль написания программ выбран таким об­разом, чтобы пользователь ПЭВМ смог без особого труда понять текст программы. В пособии приведены также варианты заданий и указания к про­ведению лабораторных работ.

I. Некоторые сведения о приближенных вычислениях

1.1.Общие сведения о погрешностях

В большинстве случаев технические вычисления производятся с при­ближенными числами. Это происходит потому, что исходные данные для чис­ленного определения какой-либо величины являются результатом измерена или наблюдения. К данным такого рода относятся, например, плотность раз­личных веществ, их теплопроводность, коэффициент линейного расширения и другие данные.

Известно, что никакое измерение не может быть произведено абсолютно точно. Любой результат измерения содержит некоторую погрешность, которая обнаруживается тем, что при повторных измерениях получается результат, отличающийся от первого. По этим отклонениям результатов измерений и судят о пределах погрешностей в них. Понятно, что погрешности исходных данных переходят и в величины, определяемые по этим данным, даже в том случае, когда вычисления проводятся по абсолютно точным формулам.

В технике для любого изделия существуют допуски, то - есть пределы погрешностей, при которых изделие признается годным. Поэтому при расче­тах (относящихся к изделиям), выполняемым по неточным исходным данным, необходимо уметь определять погрешность конечного результата, чтоб быть уверенным в не превышении погрешностью тех пределов, которые в данном вопросе допускается.

Оценка точности расчета или измерения производится на основе абсолютной и относительной погрешности результата.

I.2.Абсолютная и относительная погрешности

Абсолютной погрешностью приближенного числа а называется абсолютная величина разности между соответствующим точным числом А ичислом а, т.е.

= (I)

Здесь следует различать два случая:

I) число А известно и тогда абсолютная погрешность легко определяется по формуле (I);

2) число А не известно, что практически бывает очень часто и, сле­довательно, абсолютная погрешность не может определяться по форму­ле (І).Тогда величина принимается на основе результатов измерений величиныа.

Указание одной только абсолютной погрешности недостаточно харак­теризует достоинство результата. Если известно, например, что погрешности измерения некоторой длины составляет I мм, то нельзя сказать хорошо или плохо выполнено измерение. Для этого необходимо знать и саму измеряемую величину. Так, если бы указанная погрешность относилась к длине в I км,то можно было бы сказать, что получен исключительно точ­ный результат, а если же измерялась толщина металлического листа и вместо 3 мм намерили 2 мм, то, очевидно, такое измерение никуда не годится.

Поэтому достоинство результата измерения или расчета гораздо лучше характеризуется относительной погрешностью, представляющей собой отношение абсолютной погрешности к самому значению величины, т.е.

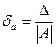
Относительная погрешность обычно выражается в процентах и записывается не более чем с двумя-тремя значащими цифрами. Чем меньше относи - тельная погрешность, тем больше точность, с которой известна какая-либо величина. Поэтому относительная погрешность принимается за меру точности измерения или результата расчета.

Например, если при изменении длин двух стержней получено L₁= 100,8 см 0,1 см и L₂= 5,2 см ± 0,1 см, то, несмотря на совпадение абсолютных погрешностей, качество первого измерения выше, чем второго. Для первого измерения относительная погрешность составляет δ ₁ =0,1 : 10О,7 ≈ О, 1%, а для второго δ ₂ = 0,1 : 5,1 ≈ 2 %

1.3. Значащая цифра. Число верных знаков

Запись приближенных чисел в виде α ± _а неудобна, поэтому в прак­тике инженерных расчетов применяют такую форму записи, что только по ней можно судить о величине погрешности. Обычно о точности приближенно числа судят по количеству значащих цифр в десятичном представлении этого числа. Поэтому следует четко определить, что такое значащая цифра.

Определение. Значащей цифрой приближенного числа называется любая цифра в его десятичном изображении, отличная от нуля, и нуль, если он находится между значащими цифрами или справа от них. Все остальные нули, входящие в состав приближенного числа и служащие лишь для обозначения его десятичных разрядов, не принадлежат к значащим цифрам.

Например, в числе 0,002080 первые три нуля не являются значащими цифрами, так как они служат только для установления десятичных разря­дов других цифр. Остальные два нуля являются значащими цифрами, так как первый из них находится между цифрами 2 и 8, а второй указывает, что в приближенном числе сохранен десятичный разряд 10^-6. Если же последний нуль отбросить, то получим два неравноценных числа 0.00208и 0.002080,так как первое из них содержит три значащих цифры, а второе - четыре.

При написании больших чисел нули справа могут внести неясность относительно точности. Например, рассматривая число 689000, мы не имеем

возможности по его виду судить о том, сколько в нем значащих цифр, хотя можно утверждать, что их не меньше трех. Этой неопределенности можно избежать, записав число в виде 6,89 · 10 ⁵ , если оно имеет три знача­щих цифры; или в виде 6,8900 • 1Сг,если число имеет пять значащих цифр. Такого вида запись удобна для чисел, содержащих большое количество незначащих нулей, например, 0,000000120 можно записать 1,20 • 10 ^-7.

При записи приближенных чисел не следует увлекаться количеством значащих цифр. Это количество должно быть равно количеству верных цифр плюс одна сомнительная.

Определение. Первые n значащих цифр приближенного числа называются верными, если абсолютная погрешность этого числа не превышает половины единицы разряда, выражаемого n-ой значащей цифрой.

Например, для точного числа A=35.97 число 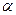= 36,00 является приближением с тремя верными знаками, так как | A-а | = 0,03 < 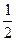· 0,1.

Число е = 2,71828 ... обычно записывается короче: 2,718 . Это означает, что его абсолютная погрешность не более 0,0005, т.е. е = 2,718 ± 0,000.

Из этого определения следует, что точность приближенного числа за­висит не от количества всех значащих цифр, а от количества верных зна­чащих цифр. В тех случаях, когда приближенное число содержит излишнее количество неверных значащих цифр, прибегают к округление числа. Чтобы округлить число до n значащих цифр, отбрасывают все его цифры, стоящие справа от n -ой значащей цифры. При этом соблюдает следующие правила:

I) если первая из отброшенных цифр меньше 5, то оставшиеся цифры сохраняются без изменения;

2) если первая из отброшенных цифр больше 5, то к последней оставшейся цифре добавляется единица;

3) если первая из отброшенных цифр равна 5 и среди остальных от­брошенных цифр имеются не нулевыми, то последняя оставшаяся цифра увеличивается на единицу.

Очевидно, что при использовании правил округления погрешность округления не превосходит половины единицы десятичного разряда, определяемого последней оставленной значащей цифрой.

Пример I. Округляя число 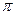= 3,1415926535...до трех, четырех и пяти значащих цифр, получим приближенные числа 3.14, 3.142, 3.1416 с абсолютными погрешностями, меньшими 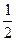· 10 ^-2 , 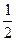· 10 ^-3 , 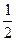· 10 ^–4.

Пример 2. Приближенное число 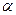= 24253 имеет относительную точ­ность 1 %. Сколько в нем верных знаков?

Определим абсолютную погрешность 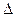= 24253 · 0,01 ≈ 243. Следова­тельно, число 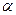имеет верными лишь первые две цифры. Согласно рассмотренным правилам, число 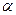следовало бы записать в виде .

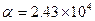1.4. Погрешность результата действий над приближенными числами

Абсолютная погрешность суммы равна сумме абсолютных погрешностей слагаемых, т.е. предельная погрешность суммы U = х₁ + х₂+...+ 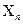равна

_U = х₁ + х₂+...+ х_n. Эта предельная погрешность достигается лишь тогда, когда ошибки всех слагаемых имеют одинаковые знаки и явля­ются наибольшими из возможных. При большом количестве слагаемых такое неблагоприятное стечение обстоятельств является маловероятным. Факти­чески ошибки отдельных слагаемых, как правило, имеют разные знаки и, следовательно, частично компенсируют друг друга, Поэтому наряду с теоре­тической предельной погрешностью суммы _U рассматривают практическую предельную погрешность, реализуемую с некоторой степенью достоверности.

В теории вероятностей доказывается, что наиболее вероятной погреш-ностью суммы будет величина . 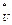= 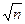, где - максимальная абсо­лютная погрешность одного слагаемого, n-число слагаемых.

Например, при сложении 100 чисел с абсолютной погрешностью 0.1 теоретическая абсолютная погрешность суммы будет равна:0.1 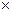100=10 фактически же можно ожидать, что эта ошибка не превзойдет величины 0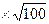.1 =1.

Аналогично в теории вероятности доказано, что предельная относительная погрешность произведения нескольких сомножителей определяется формулой , где - относительная погрешность одного со­множителя.

Совсем иная картина складывается при вычитании приближенных чисел. Рассмотрим разность двух приближенных чисел u = x₁ – x₂. Абсолют- ная погрешность разности определяется так же, как и абсолютная по­грешность суммы, т.е. u = x₁ – x₂ - абсолютная погрешность раз­ности равна сумме абсолютных погрешностей уменьшаемого и вычитаемого. Отсюда относительная погрешность разности определяется формулой

= (∆x₁ + ∆x₂ ) /А , где А - точное значение абсолютной величины разности. Если приближенные числа x₁ и x₂ близки друг к другу и имеют малые абсолютные погрешности, то число А мало. Из формулы для сле­дует, что относительная погрешность в этом случае может быть весьма большой, т.е. здесь происходит потеря точности.

Вычислим, например, разность двух чисел x₁ =47,132 и x₂ =47,III каждое из которых имеет пять верных знаков. Вычитая, полу­чаем и = 47,132 - 47,111 = 0,021. Разность и имеет лишь две зна­чащих цифры, из которых последняя сомнительная, так как предельная абсолютная погрешность разности равна

∆_u = 0,0005+0,0005 = 0,01. Найдем относительные погрешности вычитаемого, уменьшаемого и разности.

= 0.0005/47.132 ≈ 0,00001;

= 0,0005/47,111 ≈ 0,00001;

= 0.001/0,021 ≈ 0,05.

Отсюда видно, что предельная относительная погрешность раз­ности в данном примере примерно в 5000 раз больше относительных по­грешностей исходных данных. Следовательно, расчетные формулы следует преобразовывать так, чтобы в них не содержалось разностей близких чисел.

Пример. Вычислить площадь поперечного сечения тонкостенной трубы. Наружный диаметр трубы Д_н= 10 см, толщина стенки t = 2 м.

Обычно площадь кольца считают по формуле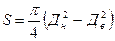

Поскольку Д и Д близки, то при вычислении разностиих квадратов происходит потеря точности. Чтобы при вычислении не было разности близких величин, формулу следует преобразовать.

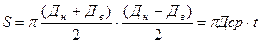,если измерены наружный диаметр и толщина стенки, то Дср = Дн – t = 10 см - 0,20 см = 9,80 см.

S = 3,14 • 9,80 • 0,20 = 0.628 • 9.80 ⁼ 6,15 см².

О погрешностях, возникающих при других арифметических опера­циях с приближенными числами, можно прочитать в (I).

В инженерных расчетах с большим количеством операций по­грешность каждой из них обычно не определяется. Но для получения ре­зультата расчета с К верными цифрами исходные данные следует брать с таким числом цифр, которые согласно рассмотренным правилам обеспечивают к + I верную цифру в результате. Результат затем округляется до К значащих цифр.