Тела и поля, определение и примеры.

КОЛЬЦА, ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ.

Кольцо

Определение 1. Непустое множество R называется кольцом, если в нем определены две алгебраические операции: сложение, ставящее в соответствие каждым двум элементам a, b элемент a + b, называемый их суммой, и умножение, ставящее в соответствие каждым двум элементам a, b элемент ab, называемый их произведением, причем эти операции обладают следующими свойствами:

I. (Коммутативность сложения) a + b = b + a;

II. (Ассоциативность сложения) a + (b + c) = (a + b) + c;

III. (Обратимость сложения) Для любых a и b из R уравнение a + x = b имеет (по крайней мере одно) решение, т. е. существует элемент 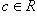такой, что a + c = b;

IV. (Коммутативность умножения) ab = ba;

Термин "кольцо" применяется также ко множествам с некоммутативным или даже неассоциативным умножением. Формулировки других свойств также меняются.

V. (Ассоциативность умножения) a(bc) = (ab)c;

VI. (Дистрибутивность умножения относительно сложения) (a + b)c = ac + bc.

Примеры колец. При обычных операциях сложения и умножения кольцом является:

1. Множество целых чисел.

2. Множество рациональных чисел.

3. Множество действительных чисел.

4. Множество рациональных чи 5. Множество, состоящее лишь из одного числа 0.

6. Множество четных чисел и вообще множество целых чисел, кратных некоторому числу n.

7. Множество комплексных чисел a + bi с целыми a и b (так называемое кольцо целых комплексных чисел).

8. Множество действительных чисел 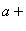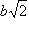, где a и b - целые числа.

Множество натуральных чисел, а также множество всех положительных рациональных чисел кольцами не являются, так как не выполняется аксиома III.

9. Большую роль в алгебре играет кольцо многочленов с одним или несколькими неизвестными и коэффициентами из некоторого кольца R.

При этом за операции сложения и умножения принимаются обычные действия над многочленами, известные из школьной алгебры. Эти действия имеют смысл, так как они сводятся к сложению и умножению коэффициентов многочленов, а последние принадлежат к кольцу R, где указанные действия определены.

10. Пары (a, b) целых чисел образуют кольцо, если операции определены по формулам

(a, b) + (c, d) = (a + c, b + d), (a, b)(c, d) = (ac, bd).

Для сложения и умножения в кольце справедливы все следствия, полученные из законов ассоциативности и коммутативности в предыдущем параграфе. В частности, можно определить сумму и произведение любого конечного числа элементов (определение 3), для которых верны правила оперирования, аналогичные (1) и которые не зависят от порядка данных элементов.

Свойства I - III показывают, что кольцо относительно операции сложения является коммутативной группой. Поэтому во всяком кольце существует элемент 0, называемый нулем кольца, со свойством

a + 0 = 0 + a = a

для любого a. Далее, для любого a существует противоположный элемент -a такой, что

a + (-a) = (-a) + a = 0.

сел. При совпадении слагаемых или сомножителей получаем n-кратное na или n-ю степень aⁿ элемента a. При этом степень aⁿ определена вообще лишь для натурального n, так как ее определение для 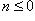требовало существование единицы и обратного элемента a ^-1, что в кольце может не выполняться. Свойства степени (3) - (5) сохраняются также лишь для натуральных показателей. В отличие от этого понятие n-кратного naэлемента a и его свойства (6) - (8) остаются верными в случае кольца (как группы по сложению) для любых целых чисел.

Из законов сложения I - III следует (как для всякой коммутативной группы) существование в любом кольце операции вычитания, обратной сложению. Умножение может и не обладать обратной операцией, как, например, в кольце целых чисел или в кольце многочленов.

ТЕЛА И ПОЛЯ, ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ.

Определение поля

Полем 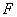называют коммутативное кольцо с единицей, в котором каждый ненулевой элемент имеет мультипликативный обратный элемент (т.е. обратный по умножению).

Другими словами, полем называют множество, которое является аддитивной абелевой группой; ненулевые же элементы этого множества образуют мультипликативную абелевую группу, и выполняется закон дистрибутивности.

По аналогии с группами число элементов поля называется порядком поля. Поля, порядки которых конечны, называются конечными полями. Конечные поля имеют наибольшее значение в теории кодирования.

Отметим некоторые свойства полей, вытекающие из их определения.

1. Для любого элемента поля .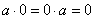

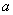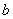2. Для ненулевых элементов и поля .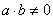

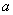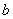3. Для любых элементов и поля .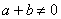

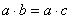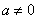4. Если и , то .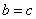

Пример 5.10Множество всех действительных чисел образует поле. Существует также поле комплексных чисел, поле рациональных чисел, но не может быть поля целых чисел, поскольку обратные элементы по умножению, кроме единицы, не являлись бы целыми.

Пример 5.11. Множество чисел 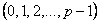, где 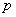– простое число, образует конечное поле, в котором сложение и умножение производятся по модулю .

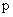Пример 5.12. При имеем простейшее двоичное поле, состоящее из двух элементов 0 и 1. Эти элементы являются соответственно единичными элементами относительно операций сложения и умножения по модулю 2, которые определяются правилами: ; ; ; ; . Так как , то операции сложения и вычитания в двоичном поле совпадают, а так как , также совпадают операции умножения и деления. Это поле находит широкое применение в теории и технике помехоустойчивого кодирования. Более сложные конечные поля рассмотрены в 5.3.5.

Тело

Те́ло — множество с двумя операциями (сложение и умножение), обладающее следующими свойствами:

· образует абелеву группу относительно сложения;

· все ненулевые элементы образуют группу относительно умножения;

· имеет место дистрибутивность умножения относительно сложения.

Свойства

· Центр тела является полем.

· Любое тело является векторным пространством над своим центром.

· Любое тело является алгеброй над своим центром.

· По теореме Веддербёрна всякое конечное тело является полем.

Примеры

· Любое поле является телом.

· Тело кватернионов {\displaystyle \mathbb {H} } .

По лемме Шура, кольцо эндоморфизмов простого модуля является телом. Каждое тело может быть получено таким образом из некоторого простого модуля.

БУЛЕВЫ АЛГЕБРЫ.

Обычная школьная алгебра работает с натуральными, целыми, рациональными и действительными числами. Таких чисел бесконечно много. А что, если взять всего лишь пару объектов и выдумать для них разные операции вроде того же сложения или умножения? Тогда мы получим новую разновидность алгебры, а при желании - много новых разновидностей, поскольку операции можно определять разными способами. Одна такая алгебра получила название "булевой" по имени ее изобретателя Дж. Буля. Операции в булевой алгебре продуманы таким образом, чтобы ее можно было использовать в логических рассуждениях.

Мы привыкли к тому, что числа применяются для обозначения количества - большего или меньшего. Но если чисел всего два, то может быть только два варианта количества,.. тогда это странно было бы называть "количеством". Поэтому те два объекта, с которыми оперирует булева алгебра, числами называть некорректно. Просто два каких-то объекта. Какие именно - зависит от области применения булевой алгебры или, как говорят математики, от интерпретации.

Булева алгебра может применяться в компьютерной технике. Здесь интерпретация заключается в том, что значок 0 означает одно напряжение между какими-нибудь контактами какой-нибудь схемы (скажем, 0 вольт), а значок 1 - другое (скажем, +5 вольт).

Второй вариант применения булевой алгебры - логические рассуждения. Здесь два объекта интерпретируются как истина (будем обозначать как true) и ложь (будем обозначать как false). Далее мы будем называть символы true и false булевыми величинами, а переменные, которые их обозначают - булевыми переменными.

Есть одна тонкость, которую люди, впервые столкнувшиеся с математической логикой, понимают с трудом. Поэтому придется сделать пространное отступление.

Что называть истиной, а что - ложью,- это вопрос, как говорится, "тонкий". Есть разные критерии истины, о которых можно долго говорить. Математическая логика подобных разговоров избегает, как говорят "абстрагируется" от них. Предполагается, что кто-то каким-то образом выяснил, что некое утверждение истинно (true), а другое - ложно (false). Неважно, как он это делает, пусть хоть Афродите молится - лишь бы выяснил. Дальше уже можно применять булеву алгебру для различных операций с этими true и false. Результат будет получен, опять же, в виде true и false. Теперь тот, кто применял булеву алгебру к откровениям Афродиты, должен сам истолковать, что же будет означать для него такая "истина" и такая "ложь".

Вот вам более привычный пример - из арифметики. В ней есть абстрактные числа, для которых заданы правила сложения, вычитания и так далее. Мы можем сложить 13 + 12 и получить 25. А вот что означают эти самые 13, 12 и 25 - это уже дело того, кто применяет арифметику. Может, это 13 килограммов картошки и 12 килограммов картошки, которые свалили в одну кучу и получили 25 килограммов. А может это обогреватель с температурой в 13 градусов тепла, который нагрели еще на 12 градусов и получили в результате обогреватель с температурой 25 градусов. Это были примеры правильного применения арифметики. А что, если сложить 12 килограммов картошки и 13 градусов тепла - что получится? 25? 25 чего? Килограммов или градусов? Наверное ни то, ни другое - ведь такое применение арифметики неправильно. Или мы можем взять 12 кучек песка и еще 13 кучек песка и высыпать их все в одно место. В результате получится вовсе не 25 кучек песка, а одна большая куча. Снова неправильное применение арифметики.

Так же и с булевой алгеброй. Можно для выяснения "истины" и "лжи" долго бить в бубен или лбом об пол. Будет достигнут некий результат... который можно подставить в формулы булевой алгебры. Потом что-то получится в процессе вычислений... и это может оказаться "истиной" или "ложью" с точки зрения специалиста по битию в бубен. Если булева алгебра будет постоянно выдавать правильные ответы (как с картошкой), тогда для этой цели она будет признана пригодной. Вопрос о том, для чего пригодна булева алгебра, а для чего - не пригодна остается за рамками самой булевой алгебры.