Свойства определителей

ТЕМА 1. МАТРИЦЫ.

Основные понятия.

Определение 1. Матрицей размерности 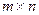(читается на ) называется прямоугольная таблица чисел, состоящая из 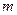строк и столбцов:

.

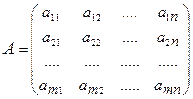Числа называются элементами матрицы 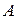, индекс указывает номер строки, индекс 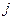- номер столбца, на пересечении которых находится элемент . Так, например, элемент 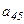стоит на пересечении четвертой строки и пятого столбца.

Для обозначения матрицы используются следующие символы:

, , , , ,

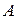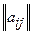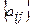Определение 2. Матрица 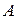называется квадратной матрицей - ого порядка, если (число строк равно числу столбцов):

.

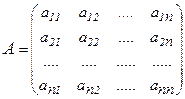Элементы , где 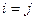, называются диагональными элементами матрицы .

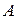Определение 3. Квадратная матрица называется диагональной, если 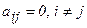(все элементы матрицы, за исключением, быть может, диагональных, равны нулю):

.

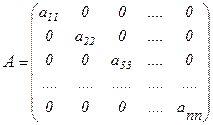Определение 4. Диагональная матрица называется единичной, если все ее диагональные элементы равны единице ( 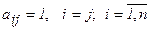). Единичная матрица обычно обозначается буквой :

.

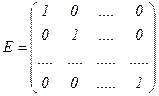Для обозначения единичной матрицы используют также символ Кронекера:

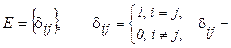символ Кронекера.

Определение 5. Матрица называется нулевой, если все ее элементы равны нулю:

.

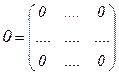Матрицей – столбцом называется матрица , состоящая из одного столбца (размерность ):

.

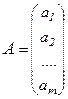Матрицей – строкой называется матрица , состоящая из одной строки (размерность ):

.

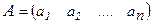Определение 6. Две матрицы и 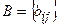называются равными, если

1) размерности матриц совпадают;

2) соответствующие элементы матриц равны:

Пусть задана матрица размерности 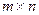. Заменим 1-ую строку на 1-ый столбец, 2-ую строку на 2-ой столбец и т.д., 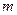-ую строку на 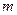-ый столбец. Такая операция называется транспонированием матрицы .

Определение 7. Матрица, полученная в результате транспонирования, называется транспонированной по отношению к матрице и обозначается символом .

Пример. Транспонировать матрицу

, .

§ 2. Определители второго и третьего порядков.

Рассмотрим матрицу 2-го порядка:

.

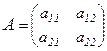Этой матрице соответствует число, которое называется определителем (детерминантом) матрицы .

Для обозначения определителя используют символы:

, .

Определение 1. Определителем 2-го порядка матрицы называется число:

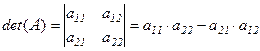. (1)

Например,

.

Введем понятие определителя 3-го порядка. Пусть

.

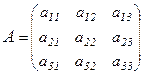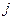Определение 2. Минором элемента матрицы называется определитель, который получается из матрицы вычеркиванием -ой строки и -ого столбца. Минор элемента 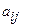обозначается символом .

Например, для элемента 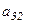матрицы минором служит определитель

.

Определение 3. Алгебраическим дополнением 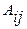элемента матрицы называется его минор, умноженный на :

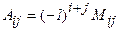. (2)

В качестве примера вычислим алгебраическое дополнение элемента 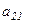матрицы

.

В нашем случае , вычеркивая 2-ую строку и 1-ый столбец, получим

, .

Определение 4. Определителем 3-го порядка матрицы называется число

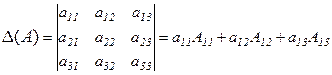. (3)

Поясним это определение на примере:

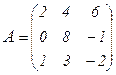, тогда

Для вычисления определителя 3-го порядка можно использовать, так называемое, «правило треугольника», а именно:

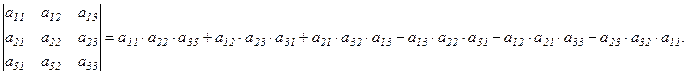Например,

.

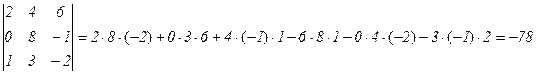§ 3. Определители n-ого порядка.

Введем теперь понятие определителя 4-ого порядка. Аналогично определениям минора и алгебраического дополнения элементов матрицы 3-го порядка, можно ввести эти понятия для элементов матрицы 4-го порядка:

,

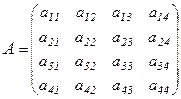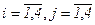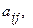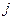понимая под минором ( ) ее элемента определитель матрицы 3-го порядка, которая получается вычеркиванием из матрицы –ой строки и –ого столбца, а под алгебраическим дополнением 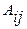– произведение

.

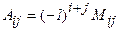Определение 1. Определителем 4-ого порядка называется число

. (1)

Аналогичным образом можно ввести понятие определителя 5-ого порядка, опираясь на определение определителя 4-ого порядка.

В общем случае, предположим, что мы определили, что такое определитель

( n- 1)-ого порядка, тогда можно ввести понятиеопределителя n-ого порядка.

Определение 2. Определитель n-ого порядка квадратной матрицы -ого порядка

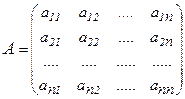
есть число

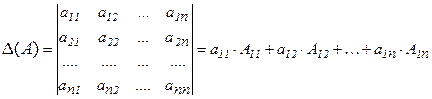, (2)

где 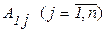- алгебраическое дополнение элемента матрицы

,

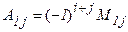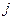- минор элемента матрицы , т.е. определитель матрицы -ого порядка, которая получается вычеркиванием из матрицы 1–ой строки и –ого столбца.

Формула (2) называется разложением определителя по элементам 1-ой строки.

В качестве примера вычислим определитель 4-ого порядка, опираясь на его определение.

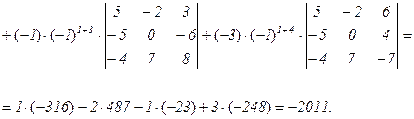
Свойства определителей.

1. При транспонировании квадратной матрицы величина ее определителя не меняется:

.

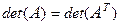2. Если поменять местами две строки (или два столбца), то определитель изменит знак на противоположный.

3. Определитель с двумя одинаковыми строками (столбцами) равен 0.

4. Определитель, содержащий нулевую строку (столбец), т.е. строку (столбец) состоящую только из нулей, равен нулю.

5. Общий множитель всех элементов строки (столбца) можно выносить за знак определителя, например,

(за знак определителя мы вынесли «2» - общий множитель элементов 1-ой строки).

6. Определитель с двумя пропорциональными строками (столбцами) равен нулю.

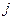7. Если каждый элемент –ой строки ( –ого столбца) определителя представлен в виде суммы двух слагаемых, то

, где

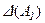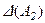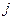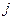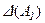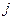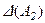в определителях и все строки (столбцы), кроме –ой строки ( –ого столбца) такие же, как и в определителе ; –ая строка ( –ый столбец) в определителе состоит из первых слагаемых –ой строки ( –ого столбца) определителя , а в определителе - из вторых слагаемых этой строки (столбца).

Поясним сказанное на примере.

.

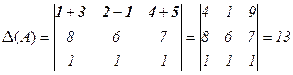В силу свойства 7

.

8. Величина определителя не изменится, если ко всем элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число.

Например,

.

Каждый элемент 2-го столбца мы умножили на «2» и прибавили к соответствующему элементу 3- его столбца. Предлагаем читателю вычислить каждый из определителей и убедиться в их равенстве.

9. Определитель равен сумме произведений элементов любой строки (столбца) на соответствующие алгебраические дополнения.

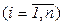, (1)

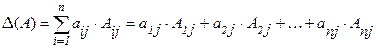, (2)

Равенство (1) называется разложением определителя по элементам –ой строки, а равенство (2) - разложением по элементам 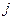-ого столбца.

10. Сумма произведений элементов строки (столбца) на алгебраические дополнения (см. определение 3 §2) элементовдругой строки (столбца) равна нулю.

Опираясь на свойства 8 и 9 можно преобразовать заданный определитель так, чтобы все элементы какой-либо строки (столбца), кроме, быть может, одного, равнялись нулю, а затем разложить определитель по элементам этой строки (столбца), что значительно облегчит вычисления.

Пример. Преобразуем определитель

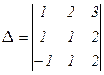
так, чтобы в первой строке все элементы, кроме, быть может, одного, стали нулями. Мысленно умножим элементы первого столбца определителя на «–3» ( 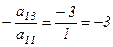) и прибавим результат к соответствующим элементам третьего столбца, получим определитель

.

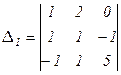Теперь умножим все элементы 1-го столбца определителя 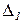на «–2» ( 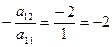) и прибавим результат к соответствующим элементам второго столбца:

.

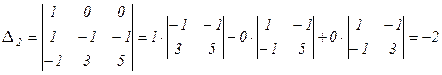В силу свойства 8

.

Алгебра матриц.

Определение 1. Суммой матриц 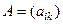и одинаковой размерности 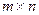называется матрица размерности 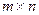, каждый элемент которой равен сумме соответствующих элементов матриц 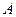и :

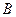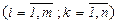, . (1)

Пример 1.

.

Определение 2. Произведением матрицы на число называется матрица размерности 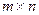, для которой ( ).

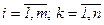Пример 2.

.
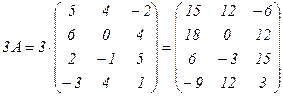