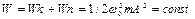Уравнения Максвелла для электромагнитного поля

Максвелл завершил формирование единой теории электромагнитного поля в её основе лежит 4 у-ния.

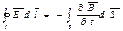1.E=E_b+E_q Поле созд за счёт электр зарядов и за счет переменных

магн полей.

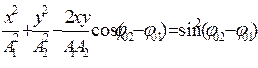2.Магнитное поле возбуждается либо движением электрических зарядов либо переменными полямя

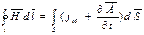
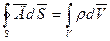3. Теорема Остраградского-Гаусса для электро статического поля в в-ве

4. Теорема Остраградского-Гаусса для магнитного поля в в-ве

45 Колебательные процессы. Виды колебаний. Свободные гармонические колебания и
их характеристики.

Колебания – процессы в той или иной мере повторяющиеся с течением времени. Свободные, вынужденные, авто колебания. От фаз: механ., эл. магн., эл. механ. Механические колебания – движения тел, которые повторяются точно или приблизительно с течением времени. Если повторение происходит через строго равные промежутки времени, то колебания называются периодическими.

Колебательная система – система тел, которая может совершать колебательные движения. У колебательной системы есть положение равновесия – положения тел, при которых они могут находиться в покое (не совершать колебаний).

Свободные колебания – колебания, возникающие в результате внутренних сил, т. е. действующих между телами колебательной системы.

Дифференциальное уравнение гармонических колебаний пружинного маятника и его решение. Характеристики колебаний пружинного маятника.

Пружинный маятник – груз, соединенный с абсолютно упругой пружиной и совершающий колебания под действием силы упругости

Уравнение гармонических колебаний пружинного маятника. Период колебаний пру­жинного маятника.

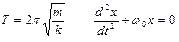, решение уравнение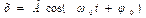

Период происходит с собственной циклической частотой 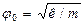F_упр = - кх

Дифференциальное уравнение гармонических колебаний физического маятника и его решение. Характеристики колебаний физического маятника.

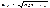Физ. маятник – твердое тело, которое вращается относительно оси, не проходящей через центр тяжести. Вращение происходит под действием силы тяжести.

Частота

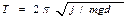Период

Математический маятник. Приведенная длина физического маятника.

материальная точка, подвешенная на невесомой нерастяжимой нити

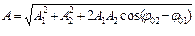
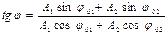
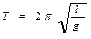Приведенная длина физического маятника – длина математического маятника, частота колебаний которого равна частоте колебаний рассматриваемого физического маятника.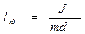

Скорость и ускорение материальной точки, совершающей гармонические колебания

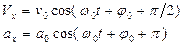
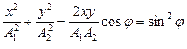
Энергия материальной точки, совершающей гармонические колебания.