Лабораторно-практические занятия

Цель лабораторно-практических занятий – не только изучить те или иные физические явления убедиться в правильности теоретических выводов, приобрести соответствующие навыки в обращении с физическими приборами, но и более глубоко овладеть теоретическим материалом. В ходе занятий студенты выполняют ряд лабораторных работ, оформляют по ним письменные отчеты, которые представляют преподавателю при сдаче зачета.

Для сдачи зачета необходимо четкое знание студентами следующих вопросов:

1. Точное определение измерявшихся величин, их определяющие формулы и их единицы измерения.

2. Схемы лабораторных установок (электрические схемы, ход лучей в оптических приборах и т.п.).

3. Точность применявшихся измерительных приборов и точность окончательного результата измерений физических величин. Знание методов обработки результатов измерений физических величин.

Экзамен

По всем разделам курса установлен один экзамен. На экзамене от студента требуется твердое знание теоретического курса, предусмотренного программой, имеющихся в нем математических выводов физических законов, ясное понимание их физической сущности, умение иллюстрировать эти законы примерами.

Кроме вопросов теоретического характера, студенту на экзамене предлагается решить задачу той же степени трудности, как т задачи, которые были в его контрольной работе.

Содержание курса физики

Введение.

Предмет физики. Метод познания в физике. Эксперименты и теории. Роль математики. Физические законы. Понятие факта в физике. Модели. Прямые и обратные задачи физики. Размерности физических величин.

Кинематика.

Движение как главная форма существования материи. Пространство и время. Способы описания состояния тела и системы тел. Системы отсчета и координат. Роль и принципы выбора систем координат. Степени свободы, инвариантные свойства числа степеней свободы. Трехмерное и многомерное пространства. Материальная точка и распространение этой модели на многомерный случай. Траектория и мировая линия, их свойства. Скорость и ускорение как производные. Поступательное и вращательное движения как основные виды движений. Угловые скорость и ускорение, нормальное и тангенциальное ускорения. Скорость и ускорение в многомерном пространстве. Инерциальные системы и равноправность покоя и равномерного прямолинейного движения. Постулат о постоянстве скорости света в вакууме. Преобразование интервалов времени и длины при больших скоростях относительных движений инерциальных систем. Парадокс близнецов. Преобразования Лоренца и релятивистское сложение скоростей. Интервал между событиями и его инвариантность.

Динамика.

Сила и масса, суперпозиция сил. Первый и второй законы Ньютона. Уравнения движения, роль начальных условий, принцип детерминизма. Примеры решения уравнений движения. Движение тел в поле сил тяготения, явление невесомости в спутниках. Динамика следящих систем, объяснение прямохождения человека. Импульс, закон сохранения импульса для механической системы, третий закон Ньютона. Взаимодействие тел через поле. Общая формулировка закона сохранения импульса. Кинетическая энергия материальной точки, связь ее с компонентами вектора импульса. Работа и потенциальная энергия. Работа перемещения материальной точки по криволинейному пути. Потенциальные силы, введение понятия потенциала для взаимодействующих тел. Потенциальная функция, потенциальная поверхность. Связь компонент силы и потенциальной функции. Потенциальная яма и условие устойчивого равновесия. Невозможность равновесия системы взаимодействующих статических точечных электрических зарядов. Принцип плотнейшей упаковки и объяснение пространственных форм кристаллов. Конформационный анализ молекул. Момент силы. Динамика вращения точки и тела вокруг постоянной оси, понятие о моменте инерции материальной точки и тела. Уравнение движения вращающегося вокруг неподвижной оси тела. Момент импульса, связь его компонент с кинетической энергией вращения. Изменение момента инерции тела при переносе оси вращения. Главные моменты инерции и устойчивость вращения тел. Закон сохранения момента импульса тела и системы тел. Особенности конструкции вертолетов. Гироскопы и их применение. Центр масс и уравнение его движения. Разделение поступательных и вращательных движений твердого тела. Пара сил. Система уравнений для движения твердого тела и его кинетическая энергия. Закон сохранения энергии и его связь с равномерностью течения времени. Движение систем со многими степенями свободы. Функция Лагранжа и уравнения Лагранжа. Принцип наименьшего действия.

Динамика больших скоростей.

Принцип относительности в физике. Релятивистский импульс. Преобразование энергии-импульса. Масса и ее связь с энергией покоя. Масса сложной системы и ее связь с энергией взаимодействия частей. Неаддитивность массы. Дефект массы и энергетика. Кинетическая энергия в релятивистской механике. Уравнение движения материальной точки в релятивистской механике. Движение материальной точки под действием постоянной силы. Скорость света как предельная скорость. Частицы с нулевой массой покоя. Принцип эквивалентности и теория происхождения сил всемирного тяготения.

Колебания и волны.

Колебания как частный случай движения, условия появления колебаний. Уравнение движения пружинного маятника и его решение. Гармоническое колебание и его характеристики. Уравнение движения физического маятника и его решение, математический маятник. Энергия гармонических колебаний. Вынужденные колебания и явление резонанса. Резонанс как проявление бифуркации. Автоколебания. Примеры проявления резонансных и автоколебательных явлений в живых организмах и технике. Резонансная передача энергии в системе одинаковых связанных маятников. Волны в упругих средах, линейные, поверхностные и объемные волны, поперечные и продольные волны, фронт волны, плоские и сферические волны. Аналитическая запись бегущей волны. Волновое уравнение. Перенос энергии бегущей волной. Сложение колебаний и волн. Когерентные источники волн. Интерференция волн от точечных когерентных источников. Условия появления максимумов и минимумов. Сложение круговых и сферических волн. Построение фронта волны по принципу Гюйгенса, поведение фронта волны в неоднородной среде. Отражение и преломление волн. Принцип Ферма. Вывод закона преломления волн на границе двух сред на основе принципа Ферма. Принцип Ферма как частный случай общего принципа минимакса. Появление отраженных волн в неоднородных средах, сложение встречных волн и образование стоячих волн. Переходное состояние и время релаксации. Связь длин стоячих волн с размерами среды, дискретность длин стоячих волн. Квантование. Управление звучанием музыкальных инструментов.

Элементы статистической и молекулярной физики.

Микроскопические и макроскопические явления. Идеальный газ как статистическая система многих частиц. Давление, объем и температура газа как обобщенные характеристики состояния газа. Равновесные и неравновесные состояния газа. Обратимые и необратимые процессы. Диаграмма давление-объем. Экспериментальные газовые законы, обобщенный газовый закон (уравнение состояния идеального газа). Вывод уравнения состояния идеального газа на основе кинетических представлений. Физический смысл понятия термодинамической температуры. Распределение энергии по степеням свободы. Распределения Максвелла и Больцмана, барометрическая формула. Неравновесные процессы. Диффузия, диффузия через мембраны, осмос, осмотическое давление и его роль в жизнедеятельности растений. Теплопередача. Внутреннее трение. Выражение неравновесных процессов через обобщенные термодинамические силы. Соотношение взаимности Онсагера. Реальные газы, уравнение Ван-дер-Ваальса, критическая точка, реальные изотермы, сжижение газов. Флуктуации и самоорганизация при фазовом переходе газ-жидкость. Жидкости, поверхностное натяжение в жидкостях, охлаждение жидкости при испарении, терморегуляция растений и животных. Смачивающие и несмачивающие жидкости. Капиллярные явления, формула Лапласа.

Элементы термодинамики.

Первое начало термодинамики, изопроцессы, адиабатический процесс, охлаждение газов при адиабатическом расширении и получение низких температур. Уравнение Пуассона и его вывод. Классическая теория теплоемкостей, причины отклонения реальных теплоемкостей как функции температуры от результатов классической теории. Работа идеального газа в различных процессах. Обратимые и необратимые циклы. Тепловые машины и цикл Карно, второе начало термодинамики. Компрессионные холодильники и тепловые насосы. Энтропия как термодинамический потенциал. Формула для энтропии идеального газа. Теорема Карно и обобщение понятия энтропии как термодинамического потенциала. Связь энтропии с микросостояниями идеального газа. Статистическое толкование энтропии. Энтропия и степень вырождения системы. Формула Больцмана. Энтропия и информация. Возрастание энтропии при необратимых процессах на примере выравнивания температуры двух находящихся в контакте нагретых тел и при выравнивании давлений в двух частях сосуда с газом. Первое и второе начала термодинамики и живые организмы. Понятие о термодинамике необратимых процессов и открытых систем. Энтропия в системе организм-окружающая среда. Производство энтропии в неравновесной среде и теорема Пригожина.

Электрические и магнитные явления.

Понятие о полях, поля скалярные и векторные. Характеристики векторных полей: напряженность, поток, циркуляция, силовые линии векторного поля. Суперпозиция полей, заряды, закон сохранения зарядов.

Взаимодействие неподвижных и движущихся зарядов, Физический смысл магнитного поля. Поле точечного заряда (закон Кулона) и системы зарядов. Поле диполя. Электростатическое поле молекулы и химические реакции. Интегральная форма закона Кулона, теорема Гаусса (первое уравнение Максвелла). Вывод формул для напряженности электростатических полей заряженного прямого провода, плоскости, конденсатора. Работа перемещения заряда в электростатическом поле, понятие потенциала. Второе уравнение Максвелла для электростатики в интегральной форме. Электрическая емкость одного проводника и двух проводников, конденсаторы, работа по зарядке конденсаторов. Энергия электростатического поля. Изменение напряженности электрического поля при введении диэлектрика, поляризуемость диэлектрика, диэлектрическая проницаемость. Изменение диэлектрической проницаемости при химических реакциях и использование этого эффекта. Электрическое поле в проводниках. Понятие о токе проводимости, вектор тока и сила тока, дифференциальная форма закона Ома. Первое правило Кирхгофа. Причина появления электрического тока в проводнике, физический смысл понятия сторонних электрических сил. Вывод закона Ома для всей цепи. Второе правило Кирхгофа. Магнитное поле прямого тока, объяснение его появления на основании релятивистских представлений. Интегральные уравнения Максвелла для постоянных магнитных полей. Примеры вычисления напряженностей магнитостатических полей. Закон Био-Савара-Лапласа. Взаимодействие полей и зарядов (токов). Формула Лоренца для силы, действующей на заряд со стороны электрического и магнитного полей. Принцип действия масс-спектрометров и их применения в химии. Индукционные явления, трансформаторы, физические принципы их действия. Экстратоки. Полная система интегральных уравнений Максвелла. Смысл членов системы уравнений Максвелла, описывающих явления, связанные с изменениями электрических и магнитных величин во времени. Взаимосвязь электрических и магнитных переменных полей, электромагнитное поле и излучение. Поля движущихся зарядов. Излучение электромагнитного поля неравномерно движущимся зарядом. "Парадокс" атома.

Электромагнитное излучение и оптика.

Свободное электромагнитное поле и его существование в виде электромагнитной волны. Поперечность электромагнитных волн. Скорость распространения электромагнитных волн и способы ее измерения. Шкала электромагнитных волн. Способы генерации и использование в науке и технике волн различных частот.

Явления, описываемые волновой теорией света. Интерференция света, условия появления статической интерференционной картины, интерференция при разделении фронта волны, просветление оптики, интерферометры и их использование. Фурье-спектрометры. Понятие о голографии. Дифракция, дифракция на щели. Фокусировка электромагнитных волн и связь размера дифракционного пятна с размерами рефлекторов. Особенности организации радиолокационной службы. Условия перехода от волновой оптики к геометрической. Зоны Френеля, зонная пластинка Френеля как фокусирующий элемент. Дифракционная решетка как диспергирующая система. Анализ состава света по длинам волн. Рентгеновская дифракция, понятие об обратных дифракционных задачах, рентгеноструктурный анализ и его особенности применительно к биологическим объектам. Пространственная структура ДНК и РНК. Дифракционный предел разрешающей способности оптических приборов.

Свет и вещество, понятие о вторичных волнах, разделение энергии на границе раздела фаз, резонансный характер взаимодействия света и вещества. Дисперсия, классическое объяснение зависимости коэффициента преломления света от длины волны падающего света. Явление двойного лучепреломления, поляризация света кристаллами. Поляризованный свет, оптическая активность, сахарометрия, использование явления вращения плоскости поляризации в молекулярной биологии. Фотоэффект и квантовая природа света. Круг явлений, объяснимых с квантовой точки зрения, микроскопическое и макроскопическое в оптике. Двойственность природы света. Законы поглощения света, понятие о нелинейных эффектах. Основные элементы конструкции спектрофотометров. Законы освещенности, зависимость освещенности от вида осветителей.

Элементы учения о строении вещества.

Особенности поведения микрочастиц. Принципы описания поведения микрочастиц, волновая функция, соотношение неопределенностей, волна де Бройля. Постулаты Бора. Уравнение Шредингера (временное и стационарное), физический смысл входящих в него членов. Решение стационарного уравнения Шредингера для частицы в одномерном потенциальном ящике и частицы на окружности. Условия появления квантовых явлений. Влияние массы и области локализации частиц. Двумерная потенциальная яма, вырождение квантовых состояний и снятие вырождения. Потенциальная яма конечной глубины и влияние ее глубины и ширины на уровни энергии частицы. Возможность локализации частицы в пространстве. Туннельный эффект. Заполнение уровней и принцип Паули, полная энергия совокупности электронов в квантовой системе. Уровни энергии в атоме водорода, переходы между уровнями. Индивидуальность спектров атомов и эмиссионный спектральный анализ. Металлическая модель молекулы и объяснение корреляции цветности вещества и эффекта сопряжения химических связей в молекулах. Нормальная и инверсная заселенность квантовых состояний. Поглощение, спонтанное и вынужденное излучения. Коэффициенты Эйнштейна. Формула Планка. Усиление света при прохождении через инверсно заселенную среду. Понятие о лазерах.

Физическая природа химической связи. Электронное строение многоэлектронных атомов, гибридизация, объяснение причин появления пространственных форм молекул. Принцип максимального перекрывания. Внутреннее вращение в молекулах и его роль в биохимических реакциях. Движение частиц в многоатомных молекулах и виды молекулярной спектроскопии. Симметрия молекул и появление правил отбора.

Фотохимические реакции и особенности потенциальных поверхностей основных и возбужденных электронных состояний в молекулах. Распад молекул при фотовозбуждениях. Физическая природа фотосинтеза. Транспорт энергии при фотосинтезе. Зонная структура электронных состояний кристаллов. Заполненные и незаполненные зоны. Уровень Ферми. Проводники, полупроводники и диэлектрики. Особенность проводимости в полупроводниках.

Систематика элементарных частиц. Законы взаимопревращений частиц, ядерные реакции, дефект массы. Строение ядер, ядерные силы, устойчивые и неустойчивые ядра, естественная и искусственная радиоактивность. Законы радиоактивного распада. Принципы радиоактивационного анализа. "Меченные" атомы в биологии. Пути использования ядерной энергии.

Примеры решения задач

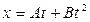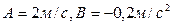Задача 1.Уравнение движения материальной точки имеет вид ,где .Определите среднее значение скорости, и ускорения в интервале времени от 2 до 4 сек.

Решение: по определению средней скорости:

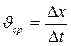
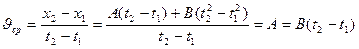
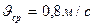
По определению среднего ускорения, оно равно:

,

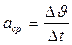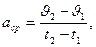
Мгновенная скорость может быть получена из уравнения

, тогда , .

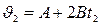Подставляя эти выражения в уравнение для среднего ускорения, получим:

.

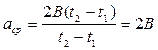То есть ускорение точки при заданном законе движения постоянно, что с очевидностью получается из уравнения движения, поскольку ускорение (его мгновенное значение) может быть получено дифференцированием уравнения движения, что дает именно такой результат:

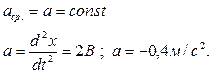
Ответ: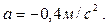

Задача 2. С какой высоты упало тело, если вторую половину своего пути оно пролетело за 1 сек ?

Решение: Проиллюстрируем задачу графически.

Поскольку в условии задачи весь, участок движения разбит на два нам необходимо будет записать два уравнения движения.

Так как на нижнем отрезке S₂ пути движение происходило с неизвестной нам начальной скоростью, рационально записать уравнения движения для всего отрезка и верхнего его участка S₁, поскольку в этих случаях начальная скорость равна нулю.

Учтем, что 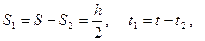тогда , .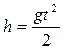

Решая эти уравнения совместно, подставляя верхнее уравнение в нижнее, получаем:

Решение этого уравнения имеет вид:

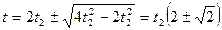
Второе решение квадратного уравнения не подходит по смыслу - все время движения не может быть меньше времени движения на втором участке пути.

Подставляя в выражение для h значение t, получаем:

.

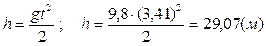Ответ: h=29,07м.

Задача 3: Человек тянет груз за веревку, при этом веревка составляет с горизонталью угол 45⁰, а коэффициент трения груза о горизонтальную поверхность, по которой он движется 0,01. Определите ускорение груза, если его масса 40 кг, а сила приложенная человеком к веревке 50 Н. Принять sin45⁰=cos45⁰=0,7.

Решение: В данном случае необходим также рисунок, иллюстрирующий условия задачи. Выберем систему отсчета таким образом, чтобы ось OX совпадала с землей, а ось OY была к ней перпендикулярна. Груз будем считать достаточно малым, чтобы его можно принять за материальную точку.

Тогда на рисунке все силы будут приложены в одной точке – центре груза.

Кроме того, необходимо спроектировать, силу тяги на оси координат и найти ее компоненты и 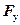. Только после этого можно записать условие задачи в аналитической форме:

Составим систему уравнений описывающих движение тела. Основное уравнение движения в векторной форме будет иметь вид:

Для решения задачи его надо записать в скалярной форме в проекциях на оси OX и OY, то есть оно распадается на два скалярных уравнения:

Кроме того, следует учесть зависимость силы трения скольжения от N. Окончательно система уравнений имеет вид:

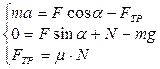
Выразив из двух последних уравнений N и F_ТР, подставим их в первое и получим окончательно:

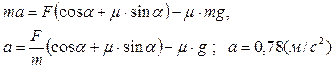
Ответ: а=0,78 м/с².

Задача 4. К шару массой 2кг и радиусом 10см прикреплен стержень массой 4,8кг и длиной 1,2м, являющийся продолжением диаметра шара. Найти момент инерции системы относительно оси, проходящей через свободный конец стержня перпендикулярно к нему.

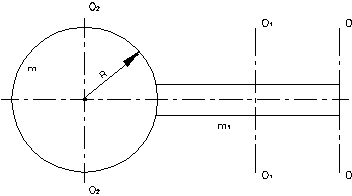Решение. Момент инерции шара относительно оси О₂О₂ проходящей через центр шара .

Момент инерции шара относительно ОО по теореме Штейнера равен:

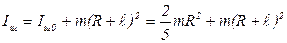
Момент инерции стержня относительно оси О₁О₁:

Момент инерции стержня относительно оси ОО по теореме Штейнера:

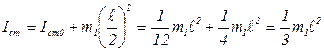
Суммарный момент инерции относительно оси ОО:

Ответ:

Задача 5. Блок имеет неподвижную ось вращения. Масса блока 1кг, радиус равен 0,2м. На блок намотана нить, к концу которой привязан груз массой 2кг. С каким ускорением будет двигаться груз?

Решение. Груз движется поступательно, IIзакон Ньютона для него имеет вид:

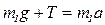
В проекции на ось у получим:

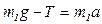(1)

Блок вращается равноускоренно, для него запишем основное уравнение динамики вращательного движения:

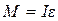(2), где 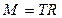(3)

Для однородного диска

(4)

Угловое ускорение связано с тангенциальным ускорением соотношением:

(5)

Подставив выражения 3, 4, 5 в уравнение (2), получим:

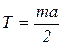(6)

Решая совместно (1) и (6), получаем:

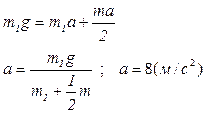
Ответ: а=8м/с².

Задача 6. Человек массой 60кг стоит на краю платформы, имеющей форму диска радиусом 1м. Момент инерции платформы 20кг·м². Платформа вместе с человеком вращается с угловой скоростью 1рад/с. Какую работу совершит человек, перейдя в центр диска? Момент инерции человека считать, как для материальной точки.

Решение. Поскольку взаимодействие происходит между человеком и платформой, систему считаем замкнутой и применяем закон сохранения момента импульса. В начальный момент времени момент инерции системы:

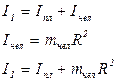
Момент импульса системы:

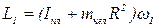
Когда человек перешел в центр платформы, его момент инерции стал равен 0, угловая скорость изменилась до ω₂, а момент импульса

По закону сохранения момента импульса:

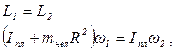
откуда

Начальная кинетическая энергия системы

Человек, перейдя в центр диска, совершил работу, что привело к изменению кинетической энергии системы, кинетическая энергия стала равной W₂ .

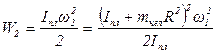
По закону сохранения энергии работа равна:

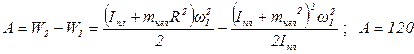(Дж)

Ответ: А=120 Дж.

Задача 7. В сосуде объемом 2м³ находится смесь 4кг гелия и 2кг водорода при температуре 27С. определить давление и молярную массу смеси газов.

Решение.Воспользуемся уравнением Клайперона – Менделеева, применив его к гелию и водороду:

(1)

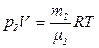(2)

где р₁ – парциальное давление гелия; m₁ – масса гелия; - его молярная масса; V - объем сосуда; Т - температура газа; R =8,31 Дж/(моль • К) - молярная газовая постоянная; p₂ - парциальное давление водорода; m₂ - масса водорода; - его молярная масса. Под парциальным давлением p₁ и р₂ понимается то давление, которое производил бы газ, если бы он только один находился в сосуде. По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси:

(3)

Из уравнения (1) и (2) выразим p₁ и р₂ подставим в уравнение (3).

Имеем

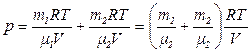(4)