Самостоятельная работа обучающегося с преподавателем 3 страница
Рассмотрим какую–либо линию на поверхности. Пусть в точке М вектор 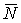 - это единичный вектор нормали к поверхности, а вектора - это единичный вектор нормали к поверхности, а вектора 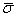 и и 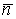 - единичные вектора касательной и главной нормали к этой линии. Рассмотрим теперь первую формулу Френе - единичные вектора касательной и главной нормали к этой линии. Рассмотрим теперь первую формулу Френе 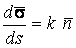 . Умножая левую и правую части равенства скалярно на . Умножая левую и правую части равенства скалярно на 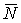 , получаем , получаем 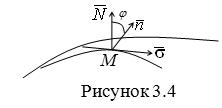 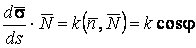 , (3.12) Где j - угол между векторами , (3.12) Где j - угол между векторами 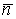 и и 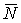 . Так как . Так как 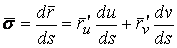 , То , То 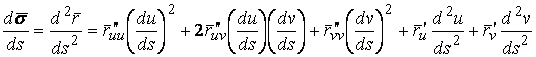 .(3.13) Величину .(3.13) Величину 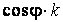 в (3.2) обозначают через в (3.2) обозначают через 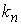 и называют Нормальной кривизной поверхности в точке М и называют Нормальной кривизной поверхности в точке М 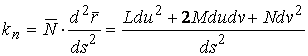 , (3.14) Где , (3.14) Где 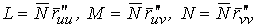 (Очевидно, что при вычислении скалярного произведения векторов (Очевидно, что при вычислении скалярного произведения векторов 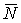 и и 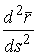 (последний вектор определяется равенством (3.13)), имеем (последний вектор определяется равенством (3.13)), имеем 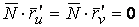 , так как вектора , так как вектора 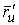 и и 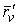 лежат в касательной плоскости к поверхности). Учтем, что единичный вектор нормали лежат в касательной плоскости к поверхности). Учтем, что единичный вектор нормали 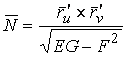 . Тогда введённые выше коэффициенты можно записать иначе . Тогда введённые выше коэффициенты можно записать иначе 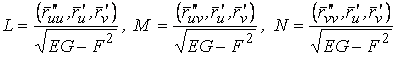 , (3.15) Где числители формул представляют собой смешанные произведения векторов, а коэффициенты E, G и F были определены ранее, формулами (3.6). Выражение, стоящее в числителе правой части формулы (3.14), называется Второй квадратичной формой поверхности (или Второй дифференциальной формой Гаусса) , (3.15) Где числители формул представляют собой смешанные произведения векторов, а коэффициенты E, G и F были определены ранее, формулами (3.6). Выражение, стоящее в числителе правой части формулы (3.14), называется Второй квадратичной формой поверхности (или Второй дифференциальной формой Гаусса) 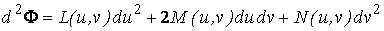 , (3.16) Итак, , (3.16) Итак,  И нормальная кривизна равна отношению двух квадратичных форм поверхности. Как вторая квадратичная форма поверхности, так и нормальная кривизна, не зависят от выбора декартовой системы координат, или от выбора криволинейных координат на поверхности. Поскольку числитель и знаменатель выражения (3.14) –это квадратичные формы относительно И нормальная кривизна равна отношению двух квадратичных форм поверхности. Как вторая квадратичная форма поверхности, так и нормальная кривизна, не зависят от выбора декартовой системы координат, или от выбора криволинейных координат на поверхности. Поскольку числитель и знаменатель выражения (3.14) –это квадратичные формы относительно 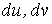 , то нормальная кривизна , то нормальная кривизна 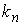 зависит только от отношения зависит только от отношения 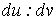 , то есть, нормальная кривизна определяется касательной к выбранной кривой на поверхности. Отсюда следует теорема. Теорема. Все линии на поверхности, проходящие через точку М поверхности с общей касательной имеют одну и ту же нормальную кривизну. Отметим также, что в так называемых Нормальных сечениях поверхности, проходящих через вектор нормали , то есть, нормальная кривизна определяется касательной к выбранной кривой на поверхности. Отсюда следует теорема. Теорема. Все линии на поверхности, проходящие через точку М поверхности с общей касательной имеют одну и ту же нормальную кривизну. Отметим также, что в так называемых Нормальных сечениях поверхности, проходящих через вектор нормали 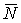 , направление этого вектора совпадает с направлением главной нормали к линии на поверхности, лежащей в этом сечении, так что нормальная кривизна совпадает с кривизной этой линии. Обычно радиус кривизны нормального сечения поверхности берется с противоположным знаком. Поскольку , направление этого вектора совпадает с направлением главной нормали к линии на поверхности, лежащей в этом сечении, так что нормальная кривизна совпадает с кривизной этой линии. Обычно радиус кривизны нормального сечения поверхности берется с противоположным знаком. Поскольку 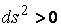 , то знак нормальной кривизны , то знак нормальной кривизны 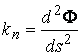 полностью определяется знаком числителя, то есть знаком второй квадратичной формы. Разделив выражение полностью определяется знаком числителя, то есть знаком второй квадратичной формы. Разделив выражение 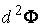 на на 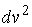 (при (при 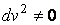 , в противном случае нужно делить на , в противном случае нужно делить на 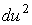 ) и обозначая ) и обозначая 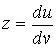 , исследуем знак получившегося квадратичного трехчлена , исследуем знак получившегося квадратичного трехчлена 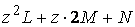 . Если . Если 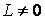 , то, разделив на L, исследуем выражение , то, разделив на L, исследуем выражение  . 1) Если . 1) Если 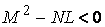 , то тогда полученное квадратичное выражение, а значит и , то тогда полученное квадратичное выражение, а значит и 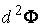 положительны. В этом случае в рассматриваемой точке знак нормальной кривизны положительны. В этом случае в рассматриваемой точке знак нормальной кривизны 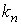 один и тот же во всех направлениях и определяется только знаком L, а главные нормали всех кривых на поверхности, проходящих через эту точку, направлены в одну сторону. Такая точка называется Эллиптической. 2) Если один и тот же во всех направлениях и определяется только знаком L, а главные нормали всех кривых на поверхности, проходящих через эту точку, направлены в одну сторону. Такая точка называется Эллиптической. 2) Если 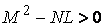 , то, в зависимости от отношения , то, в зависимости от отношения 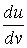 , вторая квадратичная форма , вторая квадратичная форма 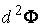 может оказаться как положительной, так и отрицательной, и нормальная кривизна может оказаться как положительной, так и отрицательной, и нормальная кривизна 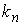 также может менять знак. Такая точка поверхности называется Гиперболической. 3)Если также может менять знак. Такая точка поверхности называется Гиперболической. 3)Если 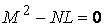 , то , то 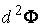 и и 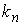 не меняют знака, но обращаются в нуль, если не меняют знака, но обращаются в нуль, если 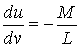 . Эта точка поверхности называется Параболической. . Эта точка поверхности называется Параболической. | ||||
| 3.5. Вторая квадратичная форма поверхности. Нормальные кривизны. Классификация точек поверхности |  |  |  | |
Рассмотрим какую–либо линию на поверхности. Пусть в точке М вектор 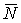 - это единичный вектор нормали к поверхности, а вектора - это единичный вектор нормали к поверхности, а вектора 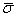 и и 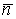 - единичные вектора касательной и главной нормали к этой линии. Рассмотрим теперь первую формулу Френе - единичные вектора касательной и главной нормали к этой линии. Рассмотрим теперь первую формулу Френе 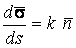 . Умножая левую и правую части равенства скалярно на . Умножая левую и правую части равенства скалярно на 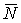 , получаем , получаем  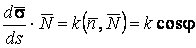 , (3.12) Где j - угол между векторами , (3.12) Где j - угол между векторами 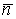 и и 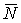 . Так как . Так как 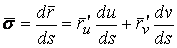 , То , То 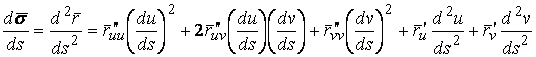 .(3.13) Величину .(3.13) Величину 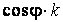 в (3.2) обозначают через в (3.2) обозначают через 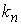 и называют Нормальной кривизной поверхности в точке М и называют Нормальной кривизной поверхности в точке М 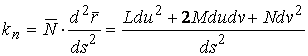 , (3.14) Где , (3.14) Где 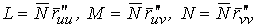 (Очевидно, что при вычислении скалярного произведения векторов (Очевидно, что при вычислении скалярного произведения векторов 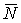 и и 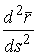 (последний вектор определяется равенством (3.13)), имеем (последний вектор определяется равенством (3.13)), имеем 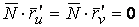 , так как вектора , так как вектора 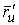 и и 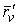 лежат в касательной плоскости к поверхности). Учтем, что единичный вектор нормали лежат в касательной плоскости к поверхности). Учтем, что единичный вектор нормали 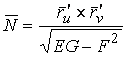 . Тогда введённые выше коэффициенты можно записать иначе . Тогда введённые выше коэффициенты можно записать иначе 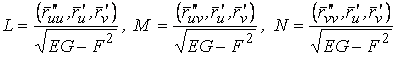 , (3.15) Где числители формул представляют собой смешанные произведения векторов, а коэффициенты E, G и F были определены ранее, формулами (3.6). Выражение, стоящее в числителе правой части формулы (3.14), называется Второй квадратичной формой поверхности (или Второй дифференциальной формой Гаусса) , (3.15) Где числители формул представляют собой смешанные произведения векторов, а коэффициенты E, G и F были определены ранее, формулами (3.6). Выражение, стоящее в числителе правой части формулы (3.14), называется Второй квадратичной формой поверхности (или Второй дифференциальной формой Гаусса) 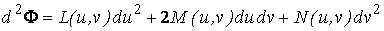 , (3.16) Итак, , (3.16) Итак,  И нормальная кривизна равна отношению двух квадратичных форм поверхности. Как вторая квадратичная форма поверхности, так и нормальная кривизна, не зависят от выбора декартовой системы координат, или от выбора криволинейных координат на поверхности. Поскольку числитель и знаменатель выражения (3.14) –это квадратичные формы относительно И нормальная кривизна равна отношению двух квадратичных форм поверхности. Как вторая квадратичная форма поверхности, так и нормальная кривизна, не зависят от выбора декартовой системы координат, или от выбора криволинейных координат на поверхности. Поскольку числитель и знаменатель выражения (3.14) –это квадратичные формы относительно 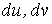 , то нормальная кривизна , то нормальная кривизна 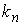 зависит только от отношения зависит только от отношения 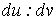 , то есть, нормальная кривизна определяется касательной к выбранной кривой на поверхности. Отсюда следует теорема. Теорема. Все линии на поверхности, проходящие через точку М поверхности с общей касательной имеют одну и ту же нормальную кривизну. Отметим также, что в так называемых Нормальных сечениях поверхности, проходящих через вектор нормали , то есть, нормальная кривизна определяется касательной к выбранной кривой на поверхности. Отсюда следует теорема. Теорема. Все линии на поверхности, проходящие через точку М поверхности с общей касательной имеют одну и ту же нормальную кривизну. Отметим также, что в так называемых Нормальных сечениях поверхности, проходящих через вектор нормали 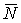 , направление этого вектора совпадает с направлением главной нормали к линии на поверхности, лежащей в этом сечении, так что нормальная кривизна совпадает с кривизной этой линии. Обычно радиус кривизны нормального сечения поверхности берется с противоположным знаком. Поскольку , направление этого вектора совпадает с направлением главной нормали к линии на поверхности, лежащей в этом сечении, так что нормальная кривизна совпадает с кривизной этой линии. Обычно радиус кривизны нормального сечения поверхности берется с противоположным знаком. Поскольку 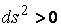 , то знак нормальной кривизны , то знак нормальной кривизны 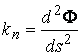 полностью определяется знаком числителя, то есть знаком второй квадратичной формы. Разделив выражение полностью определяется знаком числителя, то есть знаком второй квадратичной формы. Разделив выражение 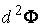 на на 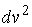 (при (при 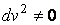 , в противном случае нужно делить на , в противном случае нужно делить на 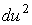 ) и обозначая ) и обозначая 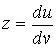 , исследуем знак получившегося квадратичного трехчлена , исследуем знак получившегося квадратичного трехчлена 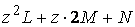 . Если . Если 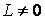 , то, разделив на L, исследуем выражение , то, разделив на L, исследуем выражение  . 1) Если . 1) Если 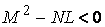 , то тогда полученное квадратичное выражение, а значит и , то тогда полученное квадратичное выражение, а значит и 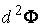 положительны. В этом случае в рассматриваемой точке знак нормальной кривизны положительны. В этом случае в рассматриваемой точке знак нормальной кривизны 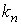 один и тот же во всех направлениях и определяется только знаком L, а главные нормали всех кривых на поверхности, проходящих через эту точку, направлены в одну сторону. Такая точка называется Эллиптической. 2) Если один и тот же во всех направлениях и определяется только знаком L, а главные нормали всех кривых на поверхности, проходящих через эту точку, направлены в одну сторону. Такая точка называется Эллиптической. 2) Если 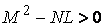 , то, в зависимости от отношения , то, в зависимости от отношения 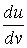 , вторая квадратичная форма , вторая квадратичная форма 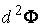 может оказаться как положительной, так и отрицательной, и нормальная кривизна может оказаться как положительной, так и отрицательной, и нормальная кривизна 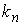 также может менять знак. Такая точка поверхности называется Гиперболической. 3)Если также может менять знак. Такая точка поверхности называется Гиперболической. 3)Если 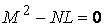 , то , то 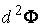 и и 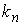 не меняют знака, но обращаются в нуль, если не меняют знака, но обращаются в нуль, если 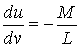 . Эта точка поверхности называется Параболической. . Эта точка поверхности называется Параболической. | |||
| 3.6. Главные направления и главные кривизны |  |  |  |
Среди бесконечного множества значений нормальной кривизны в данной точке поверхности выделим экстремальные. Это так называемые Главные кривизны. Для определения экстремальных значений нормальной кривизны используем выражение (3.14). Умножая на знаменатель, получаем 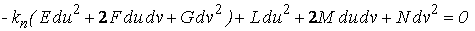 , (3.17) Отношение , (3.17) Отношение 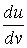 можно изменять, меняя числитель можно изменять, меняя числитель 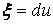 при постоянном знаменателе, или знаменатель при постоянном знаменателе, или знаменатель 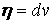 при постоянном числителе. Поэтому мы можем дифференцировать равенство (3.17) по переменной при постоянном числителе. Поэтому мы можем дифференцировать равенство (3.17) по переменной 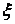 или по переменной или по переменной 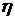 . Используем необходимые условия экстремума, приравнивая эти частные производные нулю. Получаем, сокращая на 2 . Используем необходимые условия экстремума, приравнивая эти частные производные нулю. Получаем, сокращая на 2 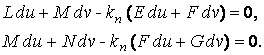 (3.18) Исключая из уравнений (3.18) величину (3.18) Исключая из уравнений (3.18) величину 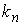 , получаем уравнение , получаем уравнение 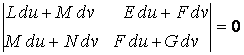 , (3.19) Которое определяет отношение , (3.19) Которое определяет отношение 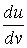 и значение и значение 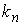 в точке экстремума. Те направления в точке поверхности, которые дают экстремум нормальной кривизне, называются Главными направлениями. Теорема.В каждой точке любой поверхности (кроме сферы) существуют в касательной плоскости два действительных, взаимно перпендикулярных главных направления. На сфере главные направления неопределенны. Здесь необходимо доказать, что квадратное уравнение (3.19) относительно в точке экстремума. Те направления в точке поверхности, которые дают экстремум нормальной кривизне, называются Главными направлениями. Теорема.В каждой точке любой поверхности (кроме сферы) существуют в касательной плоскости два действительных, взаимно перпендикулярных главных направления. На сфере главные направления неопределенны. Здесь необходимо доказать, что квадратное уравнение (3.19) относительно 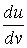 имеет действительные корни. Так как существование главных направлений не зависит от выбора координатных линий, то для упрощения вычислений будем считать координатную систему ортогональной, то есть положим имеет действительные корни. Так как существование главных направлений не зависит от выбора координатных линий, то для упрощения вычислений будем считать координатную систему ортогональной, то есть положим 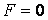 . Тогда уравнение (38) принимает вид . Тогда уравнение (38) принимает вид 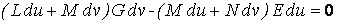 , Или , Или 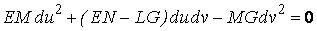 , (3.20) Дискриминант этого квадратного уравнения , (3.20) Дискриминант этого квадратного уравнения 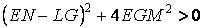 , так как , так как 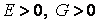 . Пусть главным направлениям отвечают решения уравнения (3.20) . Пусть главным направлениям отвечают решения уравнения (3.20) 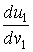 и и 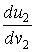 . Для доказательства ортогональности рассмотрим выражение . Для доказательства ортогональности рассмотрим выражение 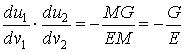 (что следует из квадратного уравнения (3.20)), откуда получим (что следует из квадратного уравнения (3.20)), откуда получим 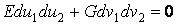 . Это совпадает с условиями ортогональности (3.10) при . Это совпадает с условиями ортогональности (3.10) при 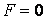 . Если М=0, то уравнение (3.20) принимает вид . Если М=0, то уравнение (3.20) принимает вид 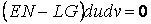 , (3.21) Тогда координатные линии , (3.21) Тогда координатные линии 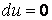 и и 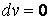 при при 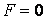 ортогональны; если же ортогональны; если же 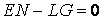 , то главные направления неопределенные (это верно для сферы). , то главные направления неопределенные (это верно для сферы). | ||||
| 3.7. Линии кривизны |
Линия, которая в каждой точке имеет касательную главного направления, называется Линией кривизны. В связи с этим определением выпишем два следствия из предыдущей теоремы. Следствие 1. Через каждую точку проходят две линии кривизны. Следствие 2. На каждой поверхности (кроме сферы) есть два семейства линий кривизны; они всегда действительны и образуют ортогональную сеть. На сфере линии кривизны неопределенные. Следствие 3. Обращение в нуль средних коэффициентов двух квадратичных форм необходимо и достаточно, чтобы поверхность была отнесена к линиям кривизны. Достаточность была доказана в разделе 2.1. Действительно, из условий 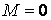 , , 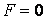 мы получили (см. равенство (3.21)), что мы получили (см. равенство (3.21)), что 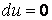 или или 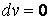 . Докажем необходимость. Если поверхность отнесена к линиям кривизны, то уравнение (3.19) допускает решения . Докажем необходимость. Если поверхность отнесена к линиям кривизны, то уравнение (3.19) допускает решения 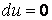 и и 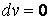 . Полагая по очереди . Полагая по очереди 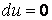 и и 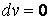 , получаем , получаем 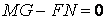 , , 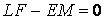 . (3.22) Рассматривая (3.22) как систему линейных алгебраических однороднх уравнений относительно . (3.22) Рассматривая (3.22) как систему линейных алгебраических однороднх уравнений относительно 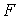 и и 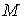 , получаем, что эта система допускает лишь тривиальное решение , получаем, что эта система допускает лишь тривиальное решение 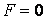 , , 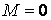 , если определитель системы не обращается в нуль, т. е. , если определитель системы не обращается в нуль, т. е. 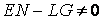 . Этот определитель равен нулю только для сферы. . Этот определитель равен нулю только для сферы. | |||
| Материалы для самостоятельной работы обучающегося Полная и средняя кривизна поверхности |
Система (3.18) является однородной и линейной относительно неизвестных 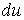 и и 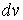 . Такая система имеет нетривиальное решение только в том случае, если ее определитель равен нулю . Такая система имеет нетривиальное решение только в том случае, если ее определитель равен нулю 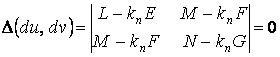 , Что приводит к квадратному уравнению относительно главных кривизн , Что приводит к квадратному уравнению относительно главных кривизн  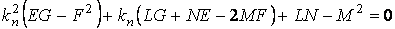 . (3.23) Используя формулы Виета, выпишем сумму и произведение главных кривизн в виде . (3.23) Используя формулы Виета, выпишем сумму и произведение главных кривизн в виде 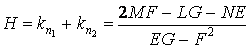 , , 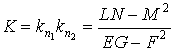 . (3.24) . (3.24) 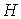 и и 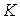 называются соответственно средней и полной (гауссовой) кривизнами поверхности. Это основные скалярные инварианты поверхности. Если говорят о поверхностях постоянной кривизны, то имеют в виду полную кривизну поверхности. Обращение в нуль средней кривизны называются соответственно средней и полной (гауссовой) кривизнами поверхности. Это основные скалярные инварианты поверхности. Если говорят о поверхностях постоянной кривизны, то имеют в виду полную кривизну поверхности. Обращение в нуль средней кривизны 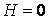 выделяет замечательный класс минимальных поверхностей, которые при заданном контуре имеют наименьшую площадь. Впервые получил эти инварианты Эйлер. выделяет замечательный класс минимальных поверхностей, которые при заданном контуре имеют наименьшую площадь. Впервые получил эти инварианты Эйлер. | |||
| 3.9. Асимптотические линии. Геодезическая кривизна. Геодезические линии |  |  |  |
Асимптотические линии на поверхности – это линии, в каждой точке которых нормальная кривизна 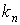 равна нулю. Это возможно, если 1) кривизна равна нулю. Это возможно, если 1) кривизна 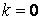 (во всех точках), в этом случае линия – прямая; 2) (во всех точках), в этом случае линия – прямая; 2) 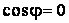 ( ( 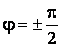 ), где ), где 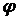 – угол между главной нормалью кривой и нормалью к поверхности. Следовательно, главная нормаль лежит в касательной плоскости к поверхности, тогда эта касательная плоскость совпадает с соприкасающейся плоскостью асимптотической линии, а нормаль к поверхности – с ее бинормалью. Поскольку – угол между главной нормалью кривой и нормалью к поверхности. Следовательно, главная нормаль лежит в касательной плоскости к поверхности, тогда эта касательная плоскость совпадает с соприкасающейся плоскостью асимптотической линии, а нормаль к поверхности – с ее бинормалью. Поскольку 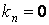 , то и , то и 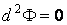 , тогда , тогда 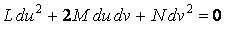 . (3.25) Условие существования действительных корней для этого уравнения . (3.25) Условие существования действительных корней для этого уравнения 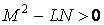 , а это означает, что асимптотические линии существуют, образуя сеть линий, только в той области поверхности, где ее кривизна отрицательна (все точки гиперболичны). Действительно, из (3.24) следует, что , а это означает, что асимптотические линии существуют, образуя сеть линий, только в той области поверхности, где ее кривизна отрицательна (все точки гиперболичны). Действительно, из (3.24) следует, что 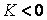 , так как , так как 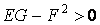 . Пример. Найти асимптотические линии геликоида, уравнения которого рассматривались ранее (раздел 3.4). Выпишем все необходимые векторы . Пример. Найти асимптотические линии геликоида, уравнения которого рассматривались ранее (раздел 3.4). Выпишем все необходимые векторы 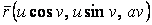 , , 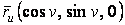 , , 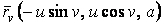 , , 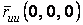 , , 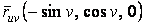 , , 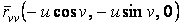 . Вычисляя далее коэффициенты первой и второй квадратичых форм по формулам (3.6) и (3.15), получим . Вычисляя далее коэффициенты первой и второй квадратичых форм по формулам (3.6) и (3.15), получим 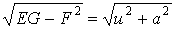 , , 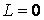 , , 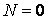 , , 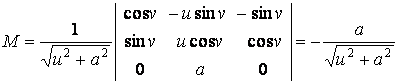 , Тогда , Тогда 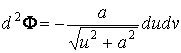 , И уравнение асимптотических линий имеет вид , И уравнение асимптотических линий имеет вид 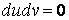 , Откуда имеем семейство , Откуда имеем семейство 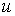 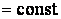 – винтовые линии и семейство – винтовые линии и семейство 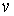 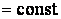 – прямолинейные образующие. Геодезическая кривизна линии на поверхности определяется формулой – прямолинейные образующие. Геодезическая кривизна линии на поверхности определяется формулой 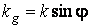 , Где , Где 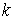 – кривизна линии, а – кривизна линии, а 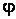 – угол между главной нормалью линии и нормалью к поверхности. Можно показать, что геодезическая кривизна линии на поверхности зависит только от линейного элемента поверхности и уравнения кривой относительно выбранного ортогонального репера. Геодезические линии – это линии с нулевой геодезической кривизной. Из формул для определения геодезической кривизны следует, что геодезическими линиями могут быть либо прямые ( – угол между главной нормалью линии и нормалью к поверхности. Можно показать, что геодезическая кривизна линии на поверхности зависит только от линейного элемента поверхности и уравнения кривой относительно выбранного ортогонального репера. Геодезические линии – это линии с нулевой геодезической кривизной. Из формул для определения геодезической кривизны следует, что геодезическими линиями могут быть либо прямые ( 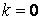 ), либо те линии, у которых ), либо те линии, у которых 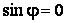 , т. е. , т. е. 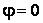 или или 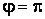 . В обоих случаях главная нормаль с точностью до положительного направления совпадает с нормалью к поверхности. Сформулируем теорему, которая здесь приводится без доказательства Теорема. Через всякую точку поверхности в области ее регулярности при заданном угле наклона касательной к направлению первой оси репера проходит одна и только одна геодезическая линия. Эта теорема аналогична теореме планиметрии: через всякую точку при заданном угле наклона к оси ОХ (заданном направлении) проходит одна и только одна прямая. Однако второе предположение планиметрии – через каждые две точки плоскости проходит одна и только одна прямая – уже не всегда удовлетворяется для геодезических линий на поверхности. В частности, противоположные точки сферы соединяются геодезическими одной длины, образующими однопараметрическое семейство. Геодезическая линия при заданном линейном элементе поверхности . В обоих случаях главная нормаль с точностью до положительного направления совпадает с нормалью к поверхности. Сформулируем теорему, которая здесь приводится без доказательства Теорема. Через всякую точку поверхности в области ее регулярности при заданном угле наклона касательной к направлению первой оси репера проходит одна и только одна геодезическая линия. Эта теорема аналогична теореме планиметрии: через всякую точку при заданном угле наклона к оси ОХ (заданном направлении) проходит одна и только одна прямая. Однако второе предположение планиметрии – через каждые две точки плоскости проходит одна и только одна прямая – уже не всегда удовлетворяется для геодезических линий на поверхности. В частности, противоположные точки сферы соединяются геодезическими одной длины, образующими однопараметрическое семейство. Геодезическая линия при заданном линейном элементе поверхности 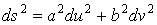 реализует кратчайшее расстояние между точками А и В По сравнению с другими линиями, проходящими на поверхности через эти точки. Это важное утверждение справедливо при выполнении двух условий: 1) кривые сравнения достаточно близки к данной геодезической; 2) точка В расположена не слишком далеко от точки А. реализует кратчайшее расстояние между точками А и В По сравнению с другими линиями, проходящими на поверхности через эти точки. Это важное утверждение справедливо при выполнении двух условий: 1) кривые сравнения достаточно близки к данной геодезической; 2) точка В расположена не слишком далеко от точки А. | |||
| 4.1. Огибающая однопараметрического семейства кривых на плоскости |  |  |  |
