Скалярное и векторное произведение векторов
Скалярное произведение двух векторов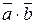 
(обозначают также 
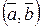) есть скаляр (число)
= 
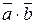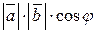, (4.8)
где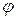 
– угол между векторами 
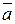и 
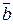(рис. 4.12).
Для острого угла между векторам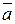и и 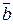их скалярное произведение 
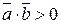, а для тупого – 
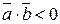. Если они взаимно перпендикулярны
( 
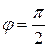), то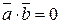 
. Для коллинеарных векторов 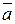и 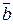скалярное произведение = 
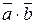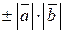, где “+” для однонаправленных векторов, а “–“ ― для противоположно направленных. В частности 
= 
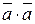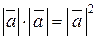, что позволяет записать длину вектора 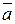в виде 
= 
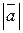(отсюда другое название длины вектора – «модуль вектора»).
Единичные базисные векторы прямоугольной декартовой системы координат удовлетворяют соотношениям: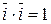 
, 
, 
, 
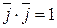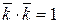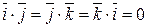. Используя эти соотношения, не трудно получить, что если векторы 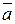и 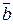заданы своими декартовыми координатами: 
, 
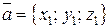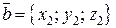, то их скалярное произведение
= 
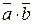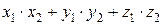. (4.9)
Из определения скалярного произведения (4.8) следует, что угол между векторами
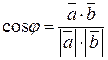. (4.10)
Свойства скалярного произведения:
= 
; 
;
; 
;
.
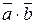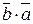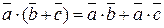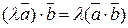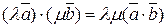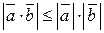Пример. Вычислить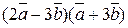 
, если 
, 
.
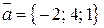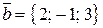◄ Используя свойства скалярного произведения, имеем =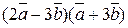 
= 
.►
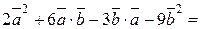
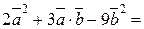
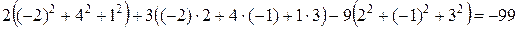Пример. Даны координаты вершин треугольника на плоскости: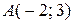 
, 
, 
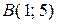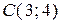. Найти угол в треугольнике при вершине 
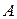и длину стороны 
.
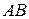◄ Проведем из вершины 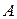векторы в вершины 
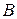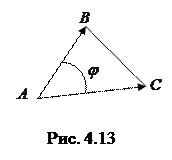
и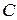 
(рис. 4.13). Тогда угол 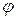при вершине 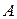будет равен углу между векторам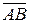и 
и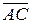 
, а длина стороны 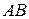равна длине вектора 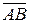. Находим координаты векторов: 
, 
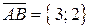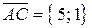. Согласно формуле (.10) 
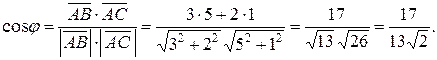Длина стороны = 
= 
. ►
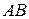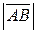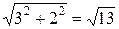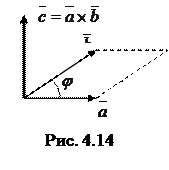Векторное произведение 
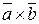(другое обозначение 
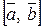) двух векторов 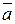и 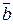есть третий вектор 
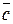, модуль которого 
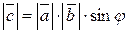(т. е. равен площади параллелограмма, построенного на векторах 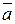и 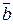), а направление перпендикулярно к обоим векторам 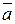и 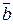(т. е. плоскости упомянутого параллелограмма) и совпадает с направлением поступательного движения правого винта при его повороте от 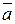к 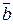на угол, меньший 
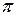(рис 4.14). Из этого определения векторного произведения следует, что векторы 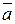, 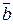и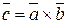 
образуют правую систему.
Если векторы 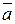и 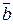коллинеарны ( 
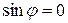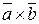), то =0.
Свойства векторного произведения:
; 
; 
;
; 
.
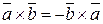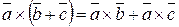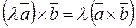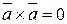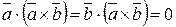Базисные единичные векторы декартовой прямоугольной системы координат удовлетворяют следующим соотношениям:
; 
; 
; 
.
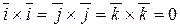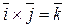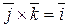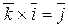Если векторы 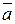и 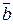заданы своими декартовыми координатами: 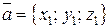, , 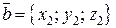то их векторное произведение
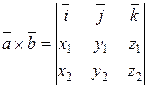. (4.11)
Смешанным (векторно – скалярным) произведением векторовназывается произведение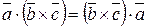 
, результатом которого является скаляр (число). Для компланарных векторов их смешанное произведение 
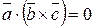. Если векторы 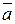, 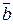и 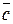образуют правую тройку, то 
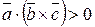, если – левую, то 
.
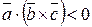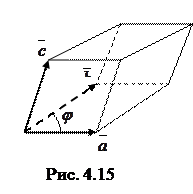Смешанное произведение 
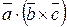равно объему параллелепипеда 
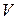, построенного на векторах 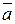, 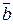и 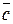(рис. 4.15), взятому со знаком “+”, если векторы 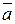, 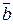и 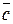образуют правую тройку, и со знаком “–“, если ― левую:
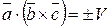. (4.12)
Если векторы 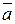, 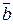и 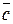заданы своими декартовыми координатами: , , 
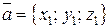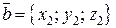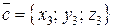, то их смешанное произведение
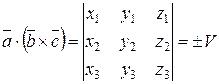(4.13)
Пример. Даны координаты вершин треугольника: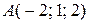 
, 
, 
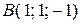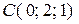. Найти площадь 
.
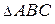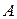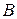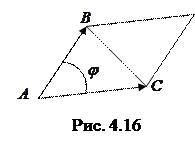
◄ Направим из вершины треугольника векторы в вершины и 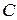(рис. 4.16). Учитывая, что площадь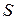 
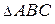равна половине площади параллелограмма, построенного на этих векторах, площадь которого, в свою очередь, можно выразить через векторное произведение, будем иметь 
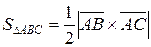. Находим координаты векторов: 
, 
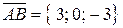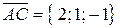. По формуле (4.11) находим векторное произведение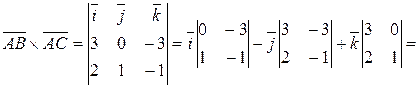 
= 
.
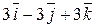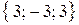Таким образом,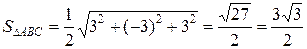 
(кв. ед.). ►
Пример. Найти объем параллелепипеда, построенного на векторах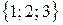 
, 
, 
.
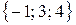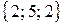◄ Искомый объем найдем по формуле (4.13). Вычисляем смешанное произведение данных векторов: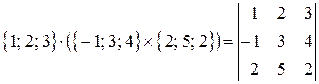 
=
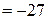. Объем параллелепипеда 
. ►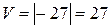