Жидкости в трубопроводах
Расчет неустановившихся течений жидкости в трубопроводах более сложен, чем расчет установившихся течений. Не существует простых алгебраических формул для вычисления параметров течения в неустановившихся течениях хотя бы потому, что таких течений существует бесчисленное множество. Поэтому расчеты неустановившихся течений, например тех, которые были поименованы в начале этого параграфа, осуществляют численно с использованием компьютеров. Приведем один из эффективных алгоритмов расчета, основанный на математическом методе, получившем название метода характеристик.
Умножим второе уравнение системы уравнений (12.14) на  и сложим результат с первым уравнением. Получим:
и сложим результат с первым уравнением. Получим:
 .
.
Аналогичным образом после вычитания второго уравнения системы (12.14), умноженного на  , из первого, получим
, из первого, получим
 .
.
Если на плоскости переменных  рассмотреть прямые линии, которые определяются уравнениями
рассмотреть прямые линии, которые определяются уравнениями


и которые называются характеристиками системы дифференциальных уравнений (12.13), можно заметить, что для любого параметра  :
:

Это означает, что выражение, стоящее слева, есть производная от функции  по направлению первой характеристики (или, как говорят, производная вдоль характеристики
по направлению первой характеристики (или, как говорят, производная вдоль характеристики  ). Аналогично
). Аналогично
 ,
,
т.е. выражение, стоящее слева, есть производная от функции  по направлению второй характеристики (или вдоль направления
по направлению второй характеристики (или вдоль направления  ).
).
Используя понятие производной по направлению, полученные уравнения можно записать в следующем виде:

или
 . (12.16)
. (12.16)
Система (12.16) называется характеристической формой системы уравнений (12.14).
Если  , то правые части уравнений в (12.15) равны нулю. Это означает, что вдоль характеристики положительного наклона (
, то правые части уравнений в (12.15) равны нулю. Это означает, что вдоль характеристики положительного наклона (  ) сохраняется величина
) сохраняется величина  , а вдоль характеристики отрицательного наклона (
, а вдоль характеристики отрицательного наклона (  ) сохраняется величина
) сохраняется величина  . Величины
. Величины  и
и 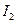 называются инвариантами Римана.
называются инвариантами Римана.
Итак, при  , т.е. при отсутствии силы трения и скатывающей составляющей силы тяжести, вдоль характеристик положительного наклона сохраняется первый инвариант Римана, а вдоль характеристики отрицательного наклона - второй инвариант Римана.
, т.е. при отсутствии силы трения и скатывающей составляющей силы тяжести, вдоль характеристик положительного наклона сохраняется первый инвариант Римана, а вдоль характеристики отрицательного наклона - второй инвариант Римана.
При  величины
величины  и
и  не сохраняются на соответствующих характеристиках. Однако формулы (12.16) могут служить для расчета различных неустановившихся течений в трубопроводе, особенно если использовать численные методы.
не сохраняются на соответствующих характеристиках. Однако формулы (12.16) могут служить для расчета различных неустановившихся течений в трубопроводе, особенно если использовать численные методы.
Пусть, например, в какой-либо момент времени  (в частности,
(в частности,  ) в трубопроводе известно распределение давлений и скоростей течения, т.е. функции
) в трубопроводе известно распределение давлений и скоростей течения, т.е. функции  и
и  . Дадим метод для расчета значений этих функций в следующий момент времени
. Дадим метод для расчета значений этих функций в следующий момент времени  , отстоящий от данного на величину
, отстоящий от данного на величину 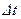 . Рассмотрим на плоскости переменных
. Рассмотрим на плоскости переменных  прямоугольную сетку с шагом
прямоугольную сетку с шагом 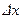 по координате и
по координате и  по времени (рис. 12.6).
по времени (рис. 12.6).

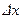






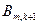






Рис. 12.6. Расчетная схема метода характеристик
Через узлы получившейся сетки проведем характеристики  и
и  положительного и отрицательного наклонов, соответственно. Непрерывное распределение искомых функций
положительного и отрицательного наклонов, соответственно. Непрерывное распределение искомых функций  и
и  заменим дискретными значениями
заменим дискретными значениями  и
и  сеточных функций в узлах построенной сетки. Предположим, что все значения
сеточных функций в узлах построенной сетки. Предположим, что все значения  и
и  известны в каком-нибудь слое
известны в каком-нибудь слое  и требуется найти значения сеточной функции при
и требуется найти значения сеточной функции при  , т.е.
, т.е.  и
и  . Покажем, как это сделать на примере произвольной точки
. Покажем, как это сделать на примере произвольной точки  .
.
Заменим производные по направлению в уравнениях (16) конечными разностями вдоль характеристик  и
и  . Получим:
. Получим:

где
 .
.
Отсюда получаем систему уравнений для определения давления  и скорости жидкости
и скорости жидкости  в точке
в точке  через известные величины этих параметров в точках
через известные величины этих параметров в точках 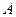 и
и 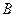 :
:

или

где  и
и  значения функции
значения функции  , вычисленные по параметрам точек
, вычисленные по параметрам точек 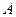 и
и 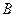 , соответственно. Из последней системы вычисляем значения
, соответственно. Из последней системы вычисляем значения  давлений и
давлений и  скоростей потока нефти в трубопроводе в момент времени
скоростей потока нефти в трубопроводе в момент времени  через значения этих же параметров в момент времени
через значения этих же параметров в момент времени  :
:
 (12.17)
(12.17)
Таким образом, рекуррентные формулы (12.17) в принципе решают поставленную задачу о расчете неустановившихся течений слабо сжимаемой жидкости в трубопроводе, поскольку позволяют рассчитать значения давлений и скоростей течения в последующий момент времени по известным значениям этих параметров в предыдущий момент времени. Так как за первый “предыдущий” момент времени можно взять начальное состояние потока (т.е. значения давлений и скоростей течения в момент времени, принимаемый за начальный  ), то вычисляя по формулам (12.17) шаг за шагом значения этих величин в последующие моменты времени, можно рассчитать параметры потока в произвольный момент времени и затем найти все интересующие нас технологические параметры нестационарного режима.
), то вычисляя по формулам (12.17) шаг за шагом значения этих величин в последующие моменты времени, можно рассчитать параметры потока в произвольный момент времени и затем найти все интересующие нас технологические параметры нестационарного режима.
