Справочный материал к заданию
Если для функции y = f(x) в точке х0 существует предел отношения приращения функции D f(x0) к приращению аргумента D x при условии D x ® 0, то этот предел называют производной функции y = f(x) в точке x0 и обозначают f ¢(x0) или y ¢(x0) , т.е.
где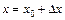 
.
Существуют и другие обозначения производной. Например 
.
Нахождение производной называют дифференцированием.
Пусть U(x) и V(x) — дифференцируемые функции, C — const, тогда правила нахождения производных имеют вид:
1. (U ± V)¢ = U ¢ ± V ¢;
2. (U · V)¢ = U ¢· V + U · V ¢;
3. (CU)¢ = CU¢;
4. 
;
5. [U(V(x))]¢ =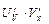 
;
6. (UV)¢ = V· UV-1 · U ¢+ UV · ln U · V ¢.
Правила дифференцирования основных элементарных функций приведены в следующей таблице:
| y = c, c = const | y¢ = 0 | y = tgx | y¢ =  |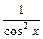
| y = xl, l ÎR | y¢ = l · xl-1 | y = ctgx | y¢ =  |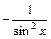
y = 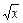 | y¢ = 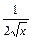 | y = arcsinx | y¢ =  |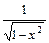
y =  | y¢ = - 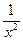 | y = arccosx | y¢ = - |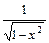
y = 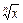 | y¢ =  | y = arctgx | y¢ =  |
| y = ex | y¢ = ex | y = arcctgx | y¢ = - |
| y = ax | y¢ = ax × lna | ||
| y = lnx | y¢ = | ||
| y = logax | y¢ =  | ||
| y = sinx | y¢ = cosx | ||
| y = cosx | y¢ = -sinx |
Рекомендации к выполнению задания
1. Прежде, чем приступить к нахождению производной, следует при необходимости привести функцию к виду, позволяющему упростить процедуру вычисления производной.
2. Особое внимание следует уделить правилу 5 дифференцирования сложной функции. В частности, любую формулу из таблицы производных можно переписать, заменив аргумент х на функцию U(x).
Например,
или
(Ul)¢ = l · U l‑–1 · U ¢.
Если же
y = U(V( 
(x))),
то
.
3. Правила 1 и 2 применимы для любого конечного числа функций.
Например,
(U ± V ± )¢ = U ¢ ± V ¢ ± ¢ ;
(U · V · )¢ = U ¢ · V · + U · V ¢ · + U · V· ¢.
Пример решения задачи
y = ln5sin(6x + 3);
Вычислим производную сложной функции,
где y = U5; U = lnV; V = sinj; j = 6x + 3,
т.е.
Можно не вводить дополнительные обозначения, определив количество промежуточных функций и перемножить их производные.
Условия задачи 4.
а) y = ln(cos4x); б) y =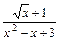 
;
а) y = arctg e3x; б) y = 
;
а) y =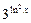 
; б) y = 
;
а) y = (arcsinx) · (x2 + 4)3; б) y = 
;
а) y =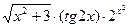 
б) y = 
;
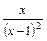а) y = x2 · tg(3x + 1); б) y =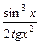 
;
а) y = 
; б) y =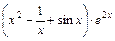 
;
а) y = 
б) y = sin2x · (3x + 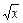– 1);
а) y =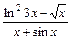 
; б) y = 
;
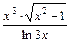а) y =еx · sinx + x · cosx; б) y = 
.
Задача 5. Найти полный дифференциал функции z=f(x,y).
Рекомендации к выполнению задания
Дифференциалом dz дифференцируемой в точке М(х,у) функции z=f(x,y) называется линейная относительно приращений Dx и Dy часть полного приращения этой функции в точке М , т. е.
dz=z'xdx+z'ydy,
где 
и 
- частные производные z по переменным x и y; dx и dy - дифференциалы х и у .
Таблицу производных ( см. п. 2 ).
Правила дифференцирования.
Пример решения задачи.
Найти полный дифференциал функции z=f(x,y)=5x2y3-3y2+6x3y-x4
1. Найдем частные производные z'x и z'y
;
.
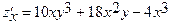2. Запишем полный дифференциал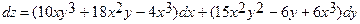 
.
Условия задачи 5.
f(x,y)=xy3-2x3y+2y4
f(x,y)=3x+2y2-5x2y2
f(x,y)=x4-6xy2-7y3
f(x,y)=2x2y-8xy2+x3=y3
f(x,y)=x3+5xy3-3x3y
f(x,y)=3x2y2+4xy3-7x3y
f(x,y)=4x5-3x2y3-6y5
f(x,y)=2xy3-4x3y-y4
f(x,y)=x3y-3xy3+y5
f(x,y)=7x-3y+5x3y2
Задача 6. Найти неопределенный интеграл функции.