Основные свойства функции

Теорема обратная теореме Виета для квадратного уравнения (с доказательством)

Теорема.

Если числа x₁ и x₂ таковы, что x₁+x₂=−p и x₁·x₂=q, то x₁ и x₂ являются корнями приведенного квадратного уравнения x²+p·x+q=0.

Доказательство.

После замены в уравнении x²+p·x+q=0 коэффициентов p и q их выражения через x₁ и x₂, оно преобразуется в равносильное уравнениеx²−(x₁+x₂)·x+x₁·x₂=0.

Подставим в полученное уравнение вместо x число x₁, имеем равенствоx₁²−(x₁+x₂)·x₁+x₁·x₂=0, которое при любых x₁ и x₂ представляет собой верноечисловое равенство 0=0, так как x₁²−(x₁+x₂)·x₁+x₁·x₂=x₁²−x₁²−x₂·x₁+x₁·x₂=0. Следовательно, x₁ – корень уравненияx²−(x₁+x₂)·x+x₁·x₂=0, а значит, x₁ – корень и равносильного ему уравненияx²+p·x+q=0.

Если же в уравнение x²−(x₁+x₂)·x+x₁·x₂=0 подставить вместо x число x₂, то получим равенство x₂²−(x₁+x₂)·x₂+x₁·x₂=0. Это верное равенство, так какx₂²−(x₁+x₂)·x₂+x₁·x₂=x₂²−x₁·x₂−x₂²+x₁·x₂=0. Следовательно, x₂ тоже является корнем уравнения x²−(x₁+x₂)·x+x₁·x₂=0, а значит, и уравненияx²+p·x+q=0.

На этом завершено доказательство теоремы, обратной теореме Виета.

Функция. Определение функции. Определение числовой функции. Способы задания функции. График функции. Область определения, область значения функции.

Функция — это соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу одного множества ставится в соответствие некоторый элемент из другого множества.

Основные свойства функции.

1. Четность и нечетность

Функция называется четной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = f(x)

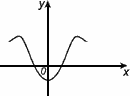
График четной функции симметричен относительно оси 0y

Функция называется нечетной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = –f(x)

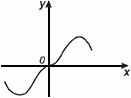
График нечетной функции симметричен относительно начала координат.

2.Периодичность

Функция f(x) называется периодической с периодом 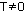, если для любого х из области определения f(x) = f(x+Т) = f(x-Т).

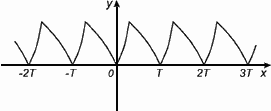
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.

3. Монотонность (возрастание, убывание)

Функция f(x) возрастает на множестве Р , если для любых x₁ и x₂ из этого множества, таких, что x₁ < x₂ выполнено неравенство f(x₁)< f(x₂).

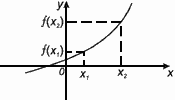
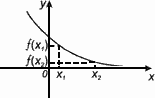
Функция f(x) убывает на множестве Р , если для любых x₁ и x₂ из этого множества, таких, что x₁ < x₂ выполнено неравенство f(x₁) > f(x₂).

4. Экстремумы

Точка Х_max называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Х_max , выполнено неравенство f(х) 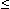f(X_max).

Значение Y_max=f(X_max) называется максимумом этой функции.

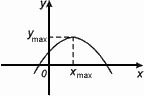
Х_max – точка максимума
У_max – максимум

Точка Х_min называется точкой минимума функции f(x) , если для всех х из некоторой окрестности Х_min , выполнено неравенство f(х) 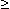f(X_min).

Значение Y_min=f(X_min) называется минимумом этой функции.

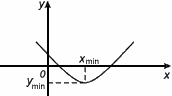
X_min – точка минимума
Y_min – минимум

X_min, Х_max – точки экстремума
Y_min, У_max – экстремумы.

5. Нули функции

Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.

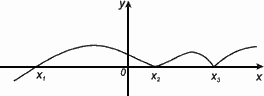
Х₁,Х₂,Х₃ – нули функции y = f(x).

Если каждому элементу 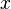из множества 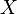по какому-либо правилу ставится в соответствие некоторый элемент 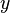из множества 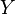, то соответствие 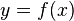называется функцией, заданной на множестве 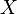со значениями из 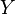. Буква 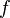в этом обозначении называется знаком функции.

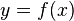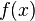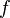Итак, функция (или кратко: или ) представляет собой тройку объектов: 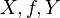, где

· множество 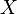называется областью задания функции;

· множество 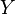называется областью значений функции;

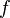· — правило, по которому каждому элементу 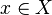сопоставляется некоторый элемент .

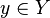Обозначенный буквой 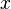каждый элемент множества 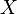называется независимой переменной или аргументомфункции. Множество 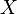при этом называется областью изменения переменной .

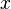Элемент 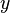, соответствующий фиксированному элементу 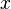называется частным значением функции в точке .

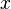Совокупность всех частных значений 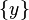называется множеством значений функции и является подмножеством области значений .

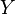Обозначенный буквой 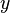каждый элемент множества 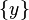есть переменная 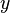с областью изменения .

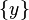Фиксированный элемент из области изменения какой-либо переменной называется значением этой переменной.

Область задания функции — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть задано.

Если на множестве 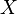задана функция, которая отображает множество 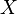в другое множество, то множество 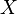называется областью задания функции.

Более формально, если задана функция 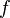, которая отображает множество 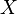в 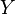, то есть: 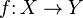, то

· множество 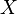называется областью задания функции 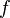и обозначается 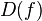, или 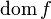(от англ. domain — «область»).

Обычно предполагается, что 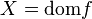. Пусть теперь 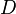— такое множество, что для каждого элемента 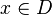задано значение функции 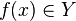, а множество 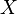содержит как множество 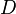так и точки, в которых функция не задана. В этом случае множество 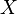называется областью отправления функции, а его подмножество 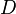называется областью задания функции.

Этот факт коротко записывают в виде: .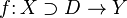

Числовая функция — это функция, принимающая значения в области вещественных чисел и которая задана на произвольном (чаще всего) метрическом пространстве

Таковы свойства

· дифференцируемости, интегрируемости, суммируемости, измеримости (для произвольных числовых функций);

а, также, свойства

· чётности (нечётности), монотонности (для вещественнозначных функций вещественного переменного);

· аналитичности, многолистности (для комплекснозначных функций комплексного переменного)

Способы задан6ия функции:

· Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.

· Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

· Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.

· Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.

график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией:

точка 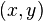располагается (или находится) на графике функции 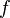тогда и только тогда, когда .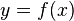