На Листе 3 рабочей книги решить систему линейных уравнений в матричном виде, сделать проверку решения.

ЛАБОРАТОРНАЯ РАБОТА 10

Тема: “Использование массивов и табличных формул”

Цель работы: изучить принцип работы с массивами и табличными функциями, ознакомиться с некоторыми встроенными функциями, которые используются для обработки матриц, закрепить на практике полученные знания.

Задание 1. На первом листе книги Еxcel выполнить четыре учебных примера (рис.1). Книгу сохранить.

Пример 1

Найти сумму чисел в строках 1 и 2 по каждому столбцу, а результат поместить в строку 3.

(см.рис.1)

Порядок выполнения:

1. В ячейках А1:Е1 и А2:Е2 разместите соответственно числа первой и второй строк.

2. Выделите интервал ячеек А3:Е3

3. Напечатайте формулу =А1:Е1+А2:Е2

4. Нажмите клавиши Сtrl+Shift+Enter, после этого должны появиться в строке формул фигурные скобки, а в ячейках А3:Е3 - результат.

Рис.1

Пример 2

Заданы два вектора -столбца x и y размерности 5. Найти скалярное произведение этих векторов.(Скалярное произведение (x, y) - это сумма произведений соответствующих элементов векторов x и y. ).

Порядок выполнения:

1. Разместим два вектора в ячейках A5:A9 и B5:B9 соответственно.

2. Выделим ячейку С8

3. Наберите формулу =СУММ(A5:A9 * B5:B9)

4. Нажмите клавиши Сtrl+Shift+Enter. Результат в ячейке С8.

5. Вычислите аналитически и сравните с полученным результатом.

Пример 3

Заданы матрицы U и V размерности 3x3. Найти их сумму.

Порядок выполнения:

1. Разместим исходные матрицы U и V в интервалах A11:C13 и E11:G13 соответственно

2. Выделим интервал размером 3 на 3 , например H11:J13

3. Наберем формулу =А11:C13+E11:G13

4. Нажмите клавиши Сtrl+Shift+Enter и в интервале Н11:J13 получим результат

5. Вычислите аналитически и сравните с полученным результатом.

Пример 4

Заданы матрицы А и B размерности 2x4 и 4x2 соответственно . Найти их произведение.

Порядок выполнения:

1. Разместим матрицы A и B в интервалах A15: D16 и F15:G18 соответственно.

2. Поскольку результат это матрица размерности 2х2 , то выделим для результата массив, содержащий две строки и два столбца, например I15:J16.

3. В строке формул наберите формулу =МУМНОЖ(A15:D16; F15:G18) или воспользуйтесь Мастером функций:

вызовите Мастер функций и выберите формулу МУМНОЖ. Нажмите кнопкуШаг>

4. Заполните поля, предназначенные для аргументов функции:

· Поле массив1 значение A15: D16

· Поле массив2значение F15:G18

5. Нажмите клавиши Сtrl+Shift+Enter

Пример 5

На Листе 2 вычислить матричное выражение 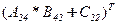двумя способами: с промежуточными результатами и в одну формулу.

Числовые значения задать как на рис.2,, оформить исходные данные, промежуточные результаты, конечный результат (см. рис. 2) . Проверить аналитически результаты вычислений

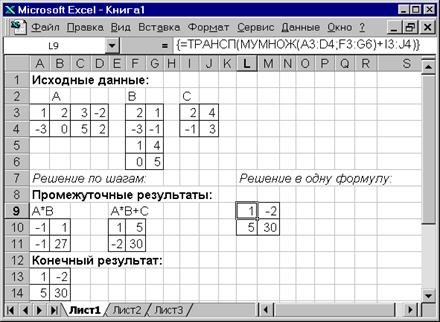
.Рис.2

Решение:

1. Поместим исходные данные – матрицы А, В и С -в ячейки A3:D4, F3:G6, I3:J4 соответственно.

Решение с промежуточными результатами:

2. Умножим матрицу А на матрицу В. Для этого:

· Выделим область ячеек для результата умножения, например A10:B11.

· С помощью команды меню 4Формцлы 4Функции открываем диалоговое окно мастера функций , выбираем в окне Категория – Математические, в окне

Функция – МУМНОЖ и нажимаем на кнопку ОК. (рис.3)

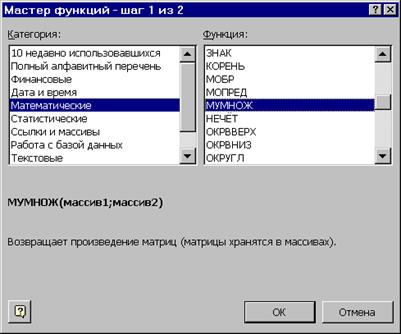
Рис.3.

· В появившемся диалоговом окне заполняем поля массив1 и массив2

· одновременно нажимаем клавиши Crtl +Shift+Enter.

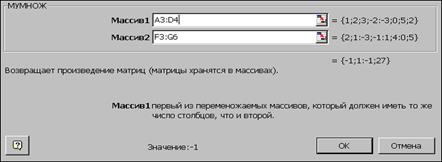
Рис.4

3. Прибавим к результату умножения матрицу С. Для этого :

· Выделим диапазон ячеек E10:F11

· Введем следующую формулу =A10:B11+I3:J4

· одновременно нажимаем клавиши Crtl +Shift+Enter

4. Транспонируем результат сложения:

· Выделим диапазон ячеек А13:В14

· С помощью команды меню 4Формулды 4Функции открываем диалоговое окно мастера функций , выбираем в окне Категория – Полный алфавитный перечень, в окне Функция – ТРАНСП, нажимаем на кнопку ОК

· В окне для аргумента функции набираем E10:F11

· одновременно нажимаем клавиши Crtl +Shift+Enter.

Решение в одну формулу:

· Выделим промежуток ячеек под результат, например L10:M11

· В строке формул наберем следующю формулу =ТРАНСП(МУМНОЖ(A3:D4;F3:G6)+I3:J4)

· Нажмем клавиши Crtl +Shift+Enter.

Пример №6

На Листе 3 рабочей книги решить систему линейных уравнений в матричном виде, сделать проверку решения.

Решение:

1. Поместим исходные данные – матрицу коэффициентов А и столбец свободных членов уравнений В - в ячейки A3:C5 и A7:A9 соответственно.( Рис.5)

2. С помощью функции МОПРЕД проверим определитель матрицы А. Если он не равен 0, то существует матрица, обратная к А.

3. Найдем матрицу, обратную к А, для этого:

· Выделим интервал ячеек , например А12:C14

· С помощью команды меню 4Формулы 4Функции открываем диалоговое окно мастера функций, выбираем в окне Категория –Математические, в окне Функция – МОБР, нажимаем на кнопку ОК

· В окне для аргумента функции набираем А3:С5

· После нажатия на кнопку ОК помещаем курсор в строку формул и одновременно нажимаем клавиши Crtl +Shift+Enter.

4. Найдем решение уравнения в виде вектора Х, для этого с помощью функции МУМНОЖ перемножим матрицу, обратную к А и вектор-столбец В.

5. Выполним проверку и убедимся, что найденный вектор Х удовлетворяет исходной системе уравнений АХ=В.

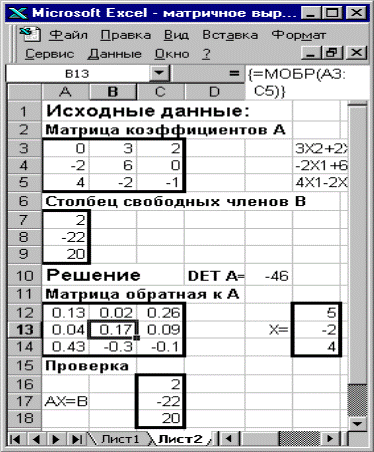
Рис.5

Задание 2.

1. На Листе 4 рабочей книги вычислить матричное выражение (вариант взять из таблицы 1). Числовые значения задать самостоятельно, оформить исходные данные, промежуточные результаты, конечный результат. Проверить аналитически результаты вычислений.

2. На Листе 5 рабочей книги решить систему линейных уравнений в матричной форме и методом Крамера. Проверить полученный результат подстановкой. Исходные данные взять из таблицы 1.

3. Листы переименовать. Сохранить файл.

Таблица 1

Номер варианта	Матричное выражение	Система линейных уравнений
	((QT34+D43)H32)T=?	X1-2X2+6X3=-28 3X1 +3X3=-6 -2X1+X2-4X3=15
	(BT23+H32)(E22+D22)=?	2X1 +X3=6 4X1-3X2-2X3=-1 2X2+7X3=12
	(QT34D34+E44)T=?	-3x1+2x3=5 2x1+4x2+4x3=-2 x1-2x2+5x3=31
	(E33+H33+DT33)Q34=?	3x2+2x3=2 -2x1+6x2=-22 4x1-2x2-x3=20
	((E44+DT44)Q43-B43)T=?	5x1+2x2+x3=21 -2x1-4x2+2x3=-2 7x2+8x3=-14
	((H34B43)T+E33-D33)T=?	6x1-2x2=18 4x1+3x2+4x3=-1 6x2+x3=-18
	((D34+B34)D43)T+E33=?	8x2+9x3=38 2x1+4x2-2x3=-14 -3x1+2x2+x3=-7
	(DT34(E33+B33+H33))T=?	2x1+4x2+x3=2 -x1+6x2+8x3=17 3x2-12x3=-54
	D43(E33+H33)T+QT34=?	-x2-4x3=-18 -8x1+2x2+2x3=12 4x1+4x2=8
	(D33+E33)T+H34Q43=?	7x1+6x2+8x3=64 2x1+3x2-5x3=-19 4x1+5x2+2x3=29
	(Q34BT34+E33-D33)T=?	9x1+7x2-x3=39 -3x2+4x3=-9 3x1+x2+9x3=9
	(E33+D33)T(Q34B43)=?	5x1+x3=25 6x1+7x2+10x3=81 -2x1+4x2+x3=1
	(D43+HT34)(E33+Q33)T=?	-x1+8x2-3x3=1 8x1+2x2=-38 -5x2+7x3=-34
	(((E44+Q44)D42)H23)T=?	-6x1+7x2-4х3=-44 3x1+6x2+6x3=57 5x1+4x2+7x3=71
	((E33+H33)T+B33)D32=?	-x1-7x2+6x3=-14 2x1+5x2+2x3=19 9x1+6x2+6x3=69