Метод дифференциального деления.

Этот способ применяют в тех случаях, когда простое деление осуществить невозможно, т. е. когда нельзя подобрать диск с нужным для простого деления числом отверстий.

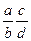Метод дифференциального деления заключается в следующем. Требуемый поворот шпинделя делительной головки получается как совокупность двух поворотов: поворота рукоятки 2(см. рис. 3, б) относительно делительного диска 1и поворота самого делительного диска, которому это движение сообщается принудительно от шпинделя делительной головки через сменные зубчатые колеса гитары.

При дифференциальном делении де­лительный диск следует освободить, вынув стопорящий его фиксатор. В зависимости от наладки делительный диск может вращаться в ту же сторону, что и рукоятка, или в противоположную. Следовательно, действительный поворот рукоятки будет больше или меньше видимого ее поворота по делительному диску.

Число оборотов рукоятки 2 головки настраивают так же,
как при простом делении, но не на требуемое число делений z,
а на близкое к нему фиктивное число делений z_ф, которое позволяет подобрать диск с нужным для деления на z_ф частей числом отверстий.
Погрешность такой наладки компенсируется настройкой диффе­-
ренциальной гитары.

Так как действительный поворот рукоятки состоит из поворота рукоятки относительно лимба и поворота самого лимба, то уравнение кинематического баланса для определения передаточного отношения дифференциальной гитары будет

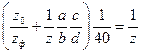
где

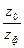- число оборотов рукоятки относительно лимба;

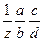- число оборотов лимба.

Сумма, взятая в скобки, выражает действительное число обо­ротов,

которое делает рукоятка при дифференциальном делении.

Из приведенной формулы можно определить передаточное

отношение сменных зубчатых колес дифференциальной гитары

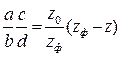или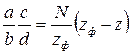

Удобнее принимать z_ф > z, так как в этом случае лимб должен вращаться в сторону вращения рукоятки, и поэтому не надо ставить в гитару дополнительное паразитное зубчатое колесо (z_Ф может быть любое составное число, по абсолютной величине близкое к z, и лучше, если оно будет делиться на z).

Пример 2. Требуется нарезать зубчатое колесо, имеющее 57 зубьев. Нужно подобрать сменные колеса гитары, ряд отверстий делительного диска и определить число оборотов рукоятки.

Пусть 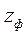= 50. Тогда число оборотов рукоятки головки при простом де­лении

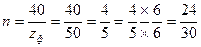
Выбирают делительный диск, имеющий окружность с 30 отверстиями, и устанавливают ножки раздвижного сектора на 24 отверстия этой окружности (считая первым отверстие, расположенное рядом с отверстием, занятым защел­кой рукоятки).

Передаточное отношение сменных колес гитары определяют по формуле

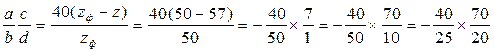
Сменные шестерни а=40, b=25, с=70 и d=20 выбираем из

прилагаемого пяткового набора: Z=20, 25, 30, 35, 40, 45,…100.

Произведем проверку:

в формулу ,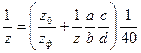

подставим данные и получим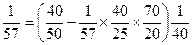

т.e. равенство справедливо, значит наладка выполнена правильно.

Так как передаточное отношение получилось отрицательным, то в гитару необходимо ввести паразитное колесо.