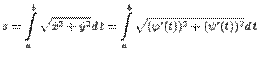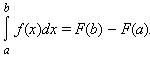Интегральное исчисление

32.Функция F(x) называется первообразной для функции f(x) на интервале X=(a,b) (конечном или бесконечном), если в каждой точке этого интервала f(x) является производной для F(x), т.е. .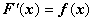

33. Неопределённый интегра́л для функции — это совокупность всех первообразных данной функции.

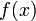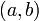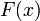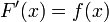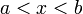Если функция определена и непрерывна на промежутке и — её первообразная, то есть при , то

,

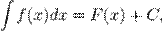
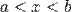где С — произвольная постоянная.

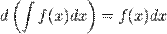
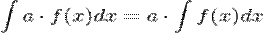
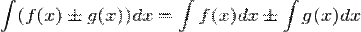
Если 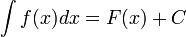, то и 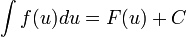, где 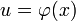— произвольная функция, имеющая непрерывную производную

34. 1°. Производная от н.и. равна подынтегральной функции, а дифференциал — подынтегральному выражению: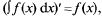

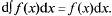
2°. 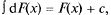в частности,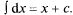

Свойства 1°, 2° следуют из определения н.и.

3°. Н.и. от алгебраической суммы конечного числа функций равен алгебраической сумме н.и. от каждого слагаемого.

Докажем, что 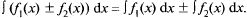(Равенство понимается с точностью до постоянного слагаемого.) Действительно, по 1°: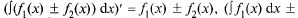

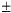
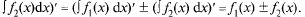Таким образом,

левая и правая части имеют одинаковые производные и могут отличаться лишь постоянной

4°. Постоянный множитель можно выносить за знак н.и.:

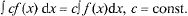
5°. Независимость вида н.и. от выбора аргумента (инвариантность формы интеграла): 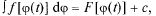где 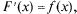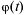имеет непрерывную производную. Действительно, по свойству инвариантности формы дифференциала: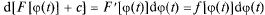

Частным случаем 5° является 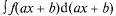= F(ax + b) + с.

Очевидно, учитывая, что d(ax + b) = a dx, получаем формулу

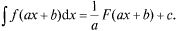
35. Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием

36.Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой. Пусть требуется вычислить интеграл 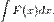Сделаем подстановку 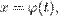где 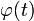— функция, имеющая непрерывную производную.Тогда 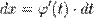и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

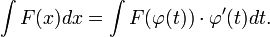
37.Интегрирование по частям — применение следующей формулы для интегрирования:

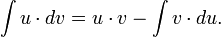
В частности, с помощью n-кратного применения этой формулы находится интеграл

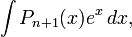
где 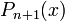— многочлен 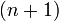-ой степени.

38. Пусть 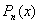и 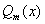некоторые полиномы степени m и n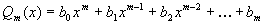 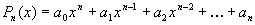Функция вида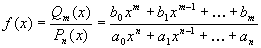

называется дробно-рациональной функцией , или коротко-рациональной дробью.

При m<n эта рациональная дробь называется правильной.

39. Интегралы вида 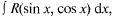где R(sin х, cos x) — рациональная функция от sin х и cos х (рациональной функцией R(u, v) называется зависимость, связывающая переменные u и v с помощью четырех арифметических операций).

Интеграл сводится к интегралу от рациональной дроби R(t) путем так называемой универсальной подстановки tg(x/2) = t,

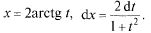Найдем, используя тригонометрические формулы, выражения для sin x и cos x через t:

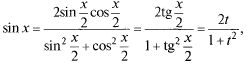
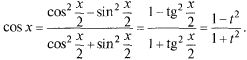
Определенный интеграл 40. Определение определённого интеграла. Пусть на отрезке [a,b] задана функция y = f(x). Разобьём отрезок [a,b] произвольным образом на n частей точками [x₀ , x₁], [x₁ , x₂], …, [x_i-1 , x_i], …, [x_n-1 , x_n]; длину i-го отрезка обозначим 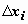: 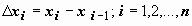; максимальную из длин отрезков обозначим 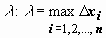. На каждом из отрезков [x_i-1 , x_i] выберем произвольную точку 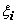и составим сумму .
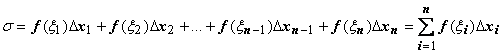Сумма 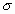называется интегральной суммой. Если существует (конечный) предел последовательности интегральных сумм 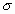при 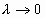, не зависящий ни от способа разбиения отрезка [a,b] на части [x_i-1 , x_i], ни от выбора точек 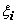, то функция f(x) называется интегрируемой по отрезку [a,b], а этот предел называется определённым интегралом от функции f(x) по отрезку [a,b] и обозначается .
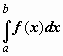Функция f(x), как и в случае неопределённого интеграла, называется подынтегральной, числа a и b - соответственно, нижним и верхним пределами интегрирования.
Кратко определение иногда записывают так: .
В этом определении предполагается, что b> a. Для других случаев примем, тоже по определению:
Если b=a, то 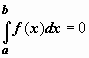; если b<a, то .

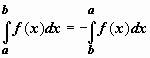41. I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. 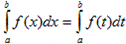, где х, t – любые буквы.

II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

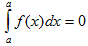
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

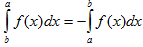
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

V. Постоянный множитель можно выносить за знак определенного интеграла.

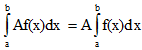
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

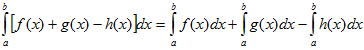
42. Одним из основных результатов математического анализа является теорема Ньютона – Лейбница:

Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда

Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).

43. ТЕОРЕМА. Пусть функция φ(t) имеет непрерывную производную на отрезке [α,β], а=φ(α), в=φ(β) и функция f(х) непрерывна в каждой точке х вида х=φ(t), где t 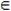[α,β].

Тогда справедливо следующее равенство:

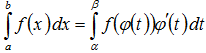
Эта формула носит название формулы замены переменной в определенном интеграле.

44.Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральнаяфункция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы

для неопределённого интеграла:

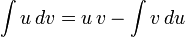
для определённого:

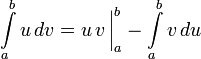
45. Пусть функция 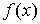непрерывна и неотрицательна на отрезке [a, b]. Тогда площадь фигуры, ограниченной осью ОХ, отрезками прямых x = a, x = b и графиком функции 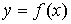, может быть вычислена по формуле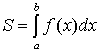 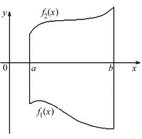Вычислить площадь фигуры, ограниченной графиками функци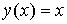й и .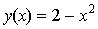

Решение. Вычислим координаты точек пересечения графиков этих функций. Для этого решим систему

=

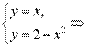
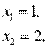
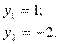
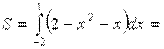
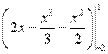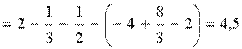
46. Для определения длины дуги 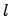необходимо вычислить определенный интеграл:

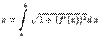
Рассмотрим случай параметрического задания кривой:

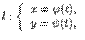
где 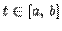. В этом случае для определения длина дуги 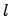вычисляется определенный интеграл: