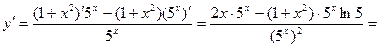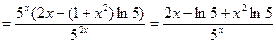Замечательные пределы
Первый замечательный предел: 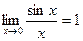 .
.
Второй замечательный предел: 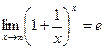 .
.
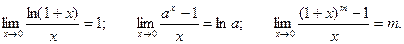
Пример 1. Вычислить пределы функции 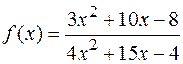 при
при
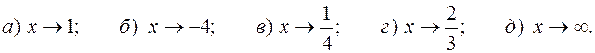
Решение.В задаче следует найти предел частного. С этой целью необходимо вычислить пределы числителя и знаменателя дроби, подставив в них предельное значение аргумента.
а) 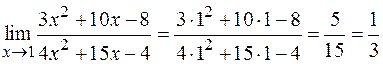 .
.
Здесь применима теорема о пределе частного.
б) 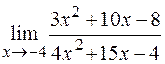 .
.
При подстановке 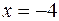 в числитель и знаменатель дроби убеждаемся, что их значения равны нулю, поэтому теорема о пределе частного здесь не применима. В данном случае говорят, что имеется неопределенность вида
в числитель и знаменатель дроби убеждаемся, что их значения равны нулю, поэтому теорема о пределе частного здесь не применима. В данном случае говорят, что имеется неопределенность вида 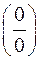 .
.
Неопределенность вида 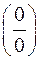 при
при 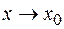 может быть раскрыта сокращением дроби на множитель вида(х–х0), который обращает числитель и знаменатель дроби в нуль, в данном случае на(х+4). Поэтому, следует разложить на множители числитель и знаменатель дроби .
может быть раскрыта сокращением дроби на множитель вида(х–х0), который обращает числитель и знаменатель дроби в нуль, в данном случае на(х+4). Поэтому, следует разложить на множители числитель и знаменатель дроби .
| 3х2+10х – 8 = 0; | 4х2+15х– 4 = 0; |
D= 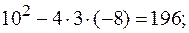 | D= 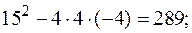 |
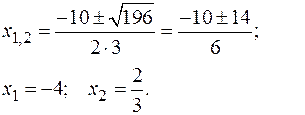 | 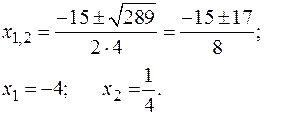 |
| 3х2+10х–8 = 3(х+4)(х–2/3) = | 4х2+15х – 4 = 4(х+4)(х–1/4 ) = |
| = (х+4)(3х–2). | = (х+4)(4х–1). |
Таким образом,
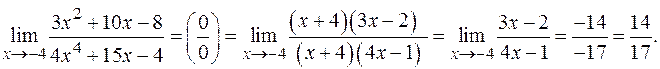
в) 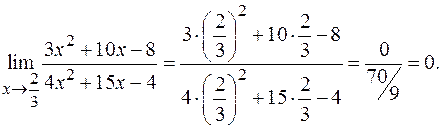
Здесь применима теорема о пределе частного, так как существуют конечные пределы числителя и знаменателя, и предел знаменателя не равен нулю.
г) 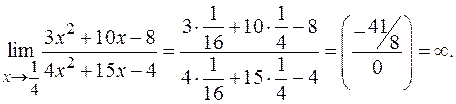
Здесь использована теорема о связи бесконечно малой и бесконечно большой функций.
д) 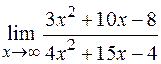 .
.
Пределы числителя и знаменателя дроби равны 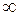 . В этом случае говорят, что имеется неопределенность вида «бесконечность на бесконечность». Теорема о пределе частного здесь не применима.
. В этом случае говорят, что имеется неопределенность вида «бесконечность на бесконечность». Теорема о пределе частного здесь не применима.
Чтобы раскрыть неопределенность вида 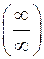 при
при 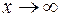 , каждый член числителя и знаменателя дроби делят на x в наивысшей степени (в нашем примере на х2), отчего величина дроби не изменится, но исчезнет неопределенность.
, каждый член числителя и знаменателя дроби делят на x в наивысшей степени (в нашем примере на х2), отчего величина дроби не изменится, но исчезнет неопределенность.
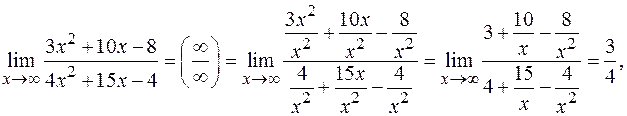
так как 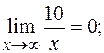
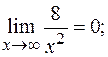
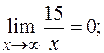
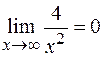
(по теореме о связи бесконечно большой и бесконечно малой функций).
Замечание. Полезно запомнить, что при 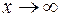 предел отношения многочленов c одинаковыми наивысшими степенями равен отношению коэффициентов при этих степенях.
предел отношения многочленов c одинаковыми наивысшими степенями равен отношению коэффициентов при этих степенях.
В нашем примере, коэффициенты при наивысшей степени х2многочленов равны 3 и 4, поэтому и предел дроби равен 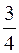 .
.
Ответы. 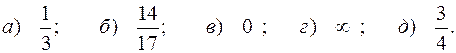
Пример 2.Найти предел 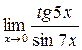 .
.
Решение. Так как tg5x ~ 5x и sin7x ~ 7x при х ® 0, то, заменив функции эквивалентными бесконечно малыми, получим:
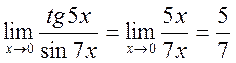
МЕТОДЫ ДИФФЕРЕНЦИАЛЬНОГО И ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
8. Дифференцирование функций одной переменной
8.1. Основные определения
8.1.1.Дифференциальное исчисление – раздел математики, в котором изучаются производные и дифференциалы функций, исследуются функции и решаются прикладные задачи (например, задачи на экстремум).
8.1.2.Дифференцирование– операции нахождения производных (частных производных) функций и их дифференциалов.
8.1.3.Дифференцируемая функция– функция одного или нескольких переменных называется дифференцируемой в некоторой точке, если в данной точке существует дифференциал этой функции. Для дифференцируемости функции необходимо и достаточно существование конечной производной для функции одной переменной или чтобы существовали в этой точке непрерывные частные производные для функции нескольких переменных.
8.1.4.Производная– основное понятие дифференциального исчисления, характеризующее скорость изменения функции 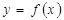 при изменении аргумента x. Пусть функция
при изменении аргумента x. Пусть функция 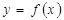 определена в некоторой окрестности точки
определена в некоторой окрестности точки 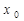 . Предел отношения приращения
. Предел отношения приращения 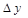 функции в этой точке (если он существует) к приращению
функции в этой точке (если он существует) к приращению 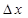 аргумента, когда
аргумента, когда 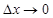 , называется производной функции
, называется производной функции 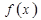 в точке
в точке 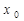 . Обозначения производной:
. Обозначения производной: 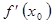 или
или 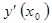 или
или 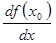 или
или 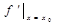 . Таким образом,
. Таким образом, 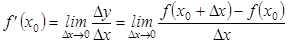 . Численно производная равна угловому коэффициенту касательной, проведённой к кривой в данной точке (тангенсу угла наклона касательной к оси Ox). Если существует производная функции
. Численно производная равна угловому коэффициенту касательной, проведённой к кривой в данной точке (тангенсу угла наклона касательной к оси Ox). Если существует производная функции 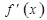 , её называют второй производной и пишут:
, её называют второй производной и пишут: 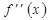 . Аналогично определяется производная любого (целого) порядка n:
. Аналогично определяется производная любого (целого) порядка n: 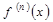 . Производная
. Производная 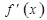 называется первой производной или производной первого порядка, вторая, третья производная и т.д. – производными высших порядков. Вычисление производной называется дифференцированием функции.
называется первой производной или производной первого порядка, вторая, третья производная и т.д. – производными высших порядков. Вычисление производной называется дифференцированием функции.
8.1.5. Производной функции 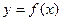 по аргументу x называется предел отношения ее приращения
по аргументу x называется предел отношения ее приращения 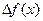 к приращению
к приращению 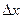 аргумента x, когда приращение аргумента стремится к нулю:
аргумента x, когда приращение аргумента стремится к нулю:
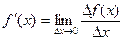 .
.
Если этот предел конечный, то функция y=f(x) называется дифференцируемой в точке x. Если же этот предел есть ∞, то говорят, что функция y=f(x) имеет в точке x бесконечную производную.
8.2. Механический смысл производной:скорость есть первая производная пути по времени, т.е. 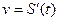 .
.
8.3. Геометрический смысл производной:тангенс угла наклона касательной к графику функции 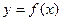 равен первой производной этой функции, вычисленной в точке касания, т.е.
равен первой производной этой функции, вычисленной в точке касания, т.е. 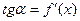
Уравнение касательной к графику функции 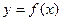 в точке
в точке 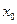 :
:
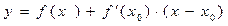
Уравнение нормали к графику функции 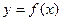 в точке
в точке 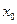 :
:
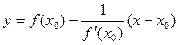
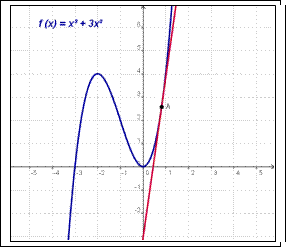
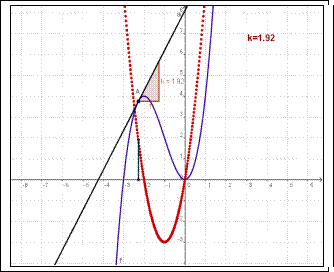
Таблица производных
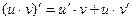 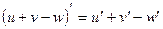 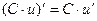 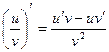 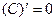 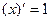 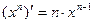 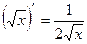 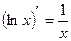 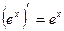 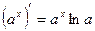 | 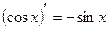 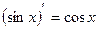 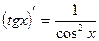 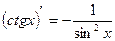 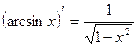 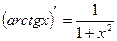 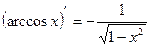 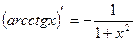 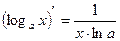 |
Рассмотрим примеры.
Найти производные функций:
Пример 1: 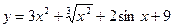
Решение: 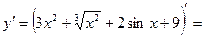
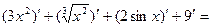
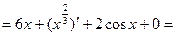
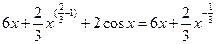 +
+
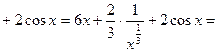
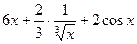
Пример 2: 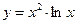
Решение: 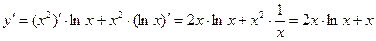
Пример 3: 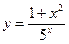
Решение: