Задания для самостоятельного выполнения. 1. Изображение орграфов с вершиной {1,2,3,4,5,6} и матрицей смежности

1. Изображение орграфов с вершиной {1,2,3,4,5,6} и матрицей смежности

Предположите, что вес каждой дуги равен 1 и найдите (если он существует)

(а) кратчайший путь (пути) от вершины 1 до вершины 2;

(б) кратчайший путь (пути) от вершины 3 до вершины 6;

(в) контур длины 5.

2. Полустепенью исхода вершины v орграфа G называется число дуг δ⁺(v) орграфа, исходящих из v, а полустепенью захода этой вершины называют число дуг δ^-(v), заходящих в нее.

Объясните, почему обе суммы — полустепеней исхода и полустепеней захода всех вершин орграфа — совпадают с числом его дуг.

Что можно сказать о числе букв И в любой строке матрицы смежности орграфа? А как проинтерпретировать их число в любом столбце?

3. Связным называется такой орграф, из которого получается связный граф, если забыть про ориентацию дуг. С другой стороны, если для любой упорядоченной пары его вершин существует путь, ведущий из первой во вторую, то такой орграф называют сильно связным.

(а) Определите, какие из связных орграфов, представленных на рис. 4.36, являются сильно связными.

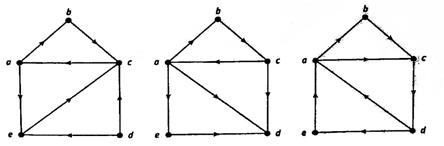
Рис 4.36.

(б) Объясните, как нужно ориентировать ребра гамильтонова графа (т. е. нарисовать на каждом ребре стрелку, превратив ее в дугу), чтобы из него получился сильно связный орграф (в) Объясните важность требования: орграф, представляющий систему односторонних дорог в городе, должен быть сильно связным.

4. Примените алгоритм топологической сортировки к (ацикличному) орграфу со следующей матрицей смежности:

Напишите новую матрицу смежности, строки и столбцы которой упорядочены в соответствии с новыми обозначениями вершин. Что можно сказать о новой матрице?

Что можно ожидать от алгоритма топологической сортировки в случае орграфа из упр. 1?

5. В табл. 4.8. приведен список действий по приготовлению цыпленка с расставленными приоритетами. Упорядочите список согласно приоритетам.

Таблица 4.8

Задания		Предварительные действия
А	Добавить лук цыпленку	И
Б	Вымыть салат-латук	Л
В	Приготовить салатную заправку	Л
Г	Перемешать жаркое	К
Д	Перемешать салат	Б, В
Е	Разрезать цыпленка	Никаких
Ж	Растереть имбирь	И
З	Подать готовое блюдо	И
И	Замариновать цыпленка	Е
К	Поставить казанок на огонь	А, Ж, З, Л
Л	Приготовить рис	Никаких

6. Пусть М = М(i, j) — матрица смежности орграфа G с множеством вершин V = {1, 2, 3, ..., п}. Напишите на псевдокоде алгоритм, вычисляющий множество антецедентов A(v)вершины v Є V.

a. Матрица смежности орграфа G имеет вид

Вычислите М², М³ и М⁴. Найдите матрицу достижимости М*.

7. С помощью алгоритма Уоршелла вычислите W₁, W₂, W₃ и W₄ для орграфа G из предыдущего упражнения, после чего найдите матрицу достижимости М*.

8. Проследите за работой алгоритма Дейкстры на примере орграфа, изображенного на рис. 4.37, и найдите кратчайшие пути до каждой вершины

(а) от вершины А;

(б) от вершины С.

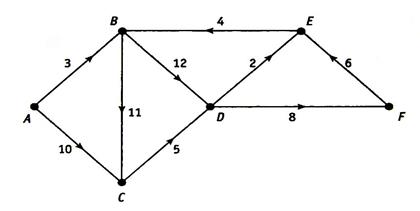
Рисунок 4.37

9. С помощью алгоритма Дейкстры найдите кратчайший путь от вершины S до всех остальных вершин в нагруженном графе из рис. 4.38. Найдите два кратчайших пути от S до Т.

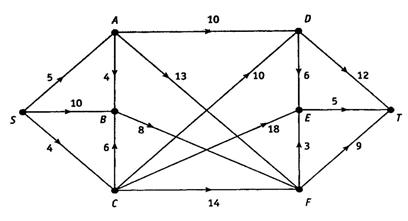
Рис. 4.38

Основные тезисы

Ориентированным графомили орграфомназывают пару G = (V, Е), где V — конечное множество вершин,а Е — отношение на V. Элементы множества Е называют дугамиорграфа.

Если uv — дуга орграфа, то вершину и называют антецедентом v.

Путемдлины kв орграфе называют такую последовательность различных вершин v₀, v₁, …, v_k, в которой каждая пара v_i-1 v_i образует дугу (i = 1,..., k).

Контуромв орграфе G принято называть последовательность вершин v₀, v_i, ..., v_{k ,} образующую путь, в которой первая v₀ совпадает с последней, а других повторяющихся вершин в ней нет.

Орграф называют бесконтурным,если в нем нет контуров. В задаче о планировании заданий соответствующий бесконтурный орграф называют системой ПЕРТ.

Последовательность согласованных метокбесконтурного орграфа G = (V, Е) — это метки: 1, 2, 3, ..., п вершин, причем если uv — дуга орграфа, соединяющая вершину и с меткой i и вершину v сметкой j, то i < j.

Для орграфа можно выписать последовательность согласованных меток тогда и только тогда, когда он не имеет контуров. Алгоритм топологической сортировкигенерирует последовательность согласованных меток бесконтурного орграфа.

Пусть G = (V, Е) — орграф с п вершинами и матрицей смежности М. Логическая степень М^к матрицы смежности хранит информацию о существовании путей длины k между произвольной парой вершин орграфа G. Матрица

М* = М илиМ² или... илиМⁿ

называется матрицей достижимостиорграфа. В ней записана информация о существовании путей между вершинами.

Алгоритм Уоршеллаиспользуется для вычисления матрицы достижимости орграфа. Алгоритм генерирует последовательность матриц W₀, W₁, W₂, …, W_n, где W₀ = M, W_n = M* а для любого k≥1 матрица W_k строится по Wk-\ следующим образом:

1. Берем k-ый столбец матрицы W_k-1.

2. Каждую строчку, у которой на k-ом месте стоит Л, переписываем в соответствующую строку матрицы W_k.

3. Каждую строчку, у которой на k-ом месте стоит И, спариваем с помощью операции илис k-ой строкой, а результат записываем в соответствующую строку матрицы W_k

Кратчайшим путеммежду произвольной парой вершин в нагруженном орграфе называется путь наименьшего общего веса. Общий вес кратчайшего пути, ведущего от вершины u к v, называется расстояниемот и до v. Если пути от и до v не существует, то расстояние между ними принято считать бесконечным и обозначать символом ∞.

Алгоритм Дейкстрыопределяет кратчайшие пути в нагруженном графе от данной вершины до любой другой.