Свойства определителей

Свойство 1. Определитель равен сумме произведений элементов любой строки (или столбца) на их алгебраические дополнения. Представление определителя в виде такой суммы называется разложением определителя по элементам строки (или столбца). Например,

–

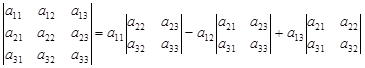– разложение определителя по элементам первой строки;

–

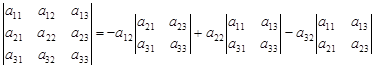– разложение определителя по элементам второго столбца.

Как видим, с помощью такого разложения вычисление определителя третьего порядка сводится к вычислению определителей второго порядка.

Пример 1.16

Вычислить определитель

.

Решение

Разложим определитель по элементам первого столбца, получим

= 8× ­– 0× +0× 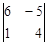= 8×(2+4) = 48.

Свойство 2. Если к элементам некоторой строки определителя прибавить соответствующие элементы другой строки, умноженные на некоторое число, то определитель не изменится.

Этим свойством можно воспользоваться для “создания” нулей в определителе и последующего применения свойства 1.

Пример 1.17

Вычислить определитель

.

Решение

К элементам первого столбца прибавим соответствующие элементы второго столбца, умноженные на (–3). Так как по свойству 2 определитель не изменится, получаем

= =14× 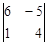=14×29 = 406.

Свойство 3. Если все элементы некоторой строки (или столбца) матрицы равны нулю, то ее определитель равен нулю. Это следует из свойства 1.

Свойство 4. Если в матрице А строки заменить столбцами, то ее определитель не изменится:

.

Свойство 5. При перестановке двух строк матрицы ее определитель меняет знак:

.

Свойство 6. Если матрица А имеет две одинаковые строки, то detA=0.

Доказательство следует из свойства 1; при перестановке двух строк матрицы знак определителя должен измениться, но, с другой стороны, определитель должен остаться прежним, так как перестановка одинаковых строк местами не изменит матрицу. Следовательно, detA= = – detA Þ detA=0.

Свойство 7. Общий множитель элементов некоторой строки (или столбца) можно выносить за знак определителя.

Рассмотрим это свойство для определителя третьего порядка. Пусть элементы третьей строки имеют общий множитель l. Тогда по свойству 7 выполняется равенство

.

Из этого равенства следует, что для умножения определителя на некоторое число l достаточно умножить на это число одну строку (или столбец) определителя (сравните с правилом умножения матрицы на число).

Решение систем линейных уравнений

По формулам Крамера

Рассмотрим систему трех линейных уравнений с тремя неизвестными

(1.15)

Обозначим D определитель матрицы 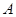: D= .

Умножим на обе части этого равенства. По свойству 7 умножение определителя на число эквивалентно умножению его строки или столбца на это число, поэтому, умножая на х₁ первый столбец, получим равенство

= .

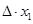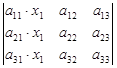Прибавим к элементам первого столбца элементы второго столбца, умноженные на 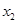, и элементы третьего столбца, умноженные на .

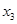По свойству 2 определитель не изменится.

D×х₁= .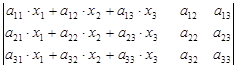

Воспользуемся системой (1.15) и элементы первого столбца полученного определителя заменим на b₁, b₂ и b₃, тогда

D×х₁= = D₁ .

Здесь D₁ обозначен последний определитель.

Таким же образом можно получить еще два аналогичных равенства, добавляя которые к последнему равенству, получаем

D×х1 = D1 ; D×х2 = D2 ; D×х3 = D3 .

(1.16)

В равенствах (1.16)

D= , D₁ = , D₂= ,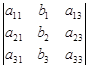

D₃ = .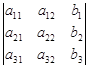

Отметим, что D –определитель матрицы 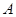, составленной из коэффициентов при неизвестных системы (1.15). Определители D₁, D₂ , D₃ получаются заменой соответственно первого, второго или третьего столбца определителя D столбцом правых частей системы (1.15).

Соотношения (1.16) называются формулами Крамера. Из них следует, что в зависимости от значений определителей возможны три случая:

1) D¹0, система имеет единственное решение. При этом значения неизвестных находятся из соотношений (1.16)

х1 = ; х2 = ; х3 = .

(1.17)

2) D = 0, а хотя бы один из определителей D₁ , D₂ или D₃ не равен нулю. В этом случае система несовместна.

3) D = D₁ = D₂ = D₃ =0.

Система имеет бесчисленное множество решений.

Пример 1.18

В качестве примера рассмотрим применение метода Крамера для решения системы двух уравнений с двумя неизвестными:

Решение

Переставим слагаемые в первом уравнении:

Вычислим определители.

D = 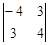= –16 – 9 = –25; D_х = 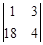= 4–54 = –50;

D_y = 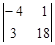= –72 – 3 = –75.

Найдем неизвестные по формулам Крамера:

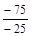= = = 2; y = = = 3.

Таким образом, решение системы (2; 3).

Пример 1.19

Решить систему 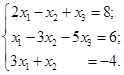по формулам Крамера.

Решение

Вычислим определители

– = 15 + 1 + 9 + 10 = 35;

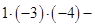
– = –20 + 6 – 12 + 40 = 14;

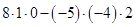– = –120 – 4 – 18 – 40 = – 182;

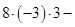
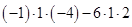– = 24–18 + 8 + 72 – 4 – 12 = 70.

Найдем неизвестные по формулам Крамера:

;

;

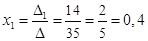Таким образом, решение системы (0,4; –5,2; 2).