Методические указания для выполнения контрольной работы по теме линейная алгебра и аналитическая геометрия
Методические указания содержат примеры решения некоторых задач по геометрии и алгебре с необходимыми теоретическими обоснованиями этих решений. Для успешного выполнения контрольной работы необходимо проработать лекции по данной дисциплине, ответить на контрольные вопросы и разобрать примеры.
Задача 1.Решить систему алгебраических уравнений по формулам Крамера и методом Гаусса: 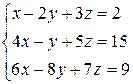 .
.
Решение.
1) Метод Крамера.
Если главный определитель системы  отличен от нуля, то система, содержащая
отличен от нуля, то система, содержащая  уравнений и
уравнений и  неизвестных, имеет единственное решение, определяемое по формулам Крамера:
неизвестных, имеет единственное решение, определяемое по формулам Крамера:
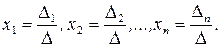
Главный определители  составлен из коэффициентов при неизвестных, побочные определители
составлен из коэффициентов при неизвестных, побочные определители  получаются из главного определителя заменой
получаются из главного определителя заменой  -го столбца столбцом свободных членов.
-го столбца столбцом свободных членов.
В заданной системе уравнений неизвестные обозначены буквами 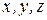 . Составим определитель системы
. Составим определитель системы  и определители
и определители  :
:

 Определитель третьего порядка задается равенством:
Определитель третьего порядка задается равенством:

 Правило «треугольников» или правило Саррюса вычисления определителей третьего порядка: первое из трех слагаемых, входящих в сумму со знаком «+», есть произведение элементов главной диагонали, второе и третье – произведение элементов, находящихся в вершинах двух треугольников с основаниями, параллельными главной диагонали. Три слагаемых, входящих в сумму со знаком «–», определяются аналогичным образом, но относительно второй (побочной диагонали).
Правило «треугольников» или правило Саррюса вычисления определителей третьего порядка: первое из трех слагаемых, входящих в сумму со знаком «+», есть произведение элементов главной диагонали, второе и третье – произведение элементов, находящихся в вершинах двух треугольников с основаниями, параллельными главной диагонали. Три слагаемых, входящих в сумму со знаком «–», определяются аналогичным образом, но относительно второй (побочной диагонали).
Определитель системы 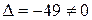 . Вычисляем побочные определители
. Вычисляем побочные определители  и, пользуясь формулами Крамера, найдем неизвестные
и, пользуясь формулами Крамера, найдем неизвестные 
2)Метод Гаусса.
Данный метод состоит в последовательном исключении неизвестных. Составим матрицу коэффициентов при неизвестных и свободных членов. С помощью элементарных преобразований над строками приведем расширенную матрицу системы к ступенчатому виду:

 .
.
Вторая матрица получена из первой путем поочередного умножения первой строки на (-4), (-6) и прибавления соответственно ко второй, третьей строке первой матрицы; третья – путем деления второй строки на (7), затем вторую строку умножаем на (-4) и прибавляем к третьей строке. В последней матрице третья строка разделена на (-7). Вертикальной чертой в матрицах отделен столбец из свободных членов.
Последней матрице соответствует система уравнений
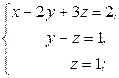
из которой, выполняя обратный ход, находим 

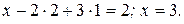
Следовательно, исходная система имеет решение 
Задача 2.Решить матричное уравнение:



Решение. Запишем данное матричное уравнение в виде  Его решением является матрица
Его решением является матрица  (если существует обратная матрица
(если существует обратная матрица  ).
).
1)Найдем определитель матрицы  :
:

Значит, обратная матрица  существует, и исходное уравнение имеет единственное решение.
существует, и исходное уравнение имеет единственное решение.
2)Найдемобратную матрицу по формуле  , где
, где  – присоединенная матрица
– присоединенная матрица 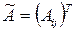 , полученная транспонированием из матрицы, составленной из алгебраических дополнений
, полученная транспонированием из матрицы, составленной из алгебраических дополнений 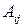 к элементам
к элементам  .
.

3)Найдем матрицу  :
:

Задача 3.Найти значение матричного многочлена  , если
, если

Решение.Если  то матричный многочлен имеет вид
то матричный многочлен имеет вид  где
где  – заданная матрица, Е–единичная матрица того же размера.
– заданная матрица, Е–единичная матрица того же размера.
1) 
2) 

Задача 4. Вычислить объем пирамиды с вершинами в точках 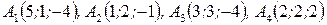 и ее высоту, опущенную из вершины
и ее высоту, опущенную из вершины  на грань
на грань 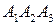 .
.
Решение. В задаче необходимо найти объем треугольной пирамиды. Искомый объем пирамиды представляет одну шестую часть объема параллелепипеда, построенного на трех векторах. Образуем векторы  ,
,  ,
, 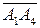 и найдем их координаты.
и найдем их координаты.
Если вектор  задан точками
задан точками 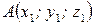 и
и  , то его координаты
, то его координаты  вычисляются по формулам
вычисляются по формулам  ,
,  ,
, 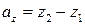 :
: 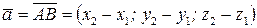 .
.
Находим координаты векторов:  ,
, 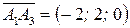 ,
, 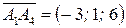 . Найдем смешанное произведение данных векторов; его модуль равен объему параллелепипеда, построенного на данных векторах:
. Найдем смешанное произведение данных векторов; его модуль равен объему параллелепипеда, построенного на данных векторах:  .
.
Объем пирамиды  . Так как объем пирамиды есть
. Так как объем пирамиды есть  , то ее высота определяется по формуле
, то ее высота определяется по формуле 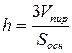 , где
, где  – площадь основания. В основании пирамиды
– площадь основания. В основании пирамиды  лежит треугольник. Площадь
лежит треугольник. Площадь  треугольника
треугольника  равна половине площади параллелограмма, построенного на векторах
равна половине площади параллелограмма, построенного на векторах  и
и  , т.е.
, т.е.  . Имеем
. Имеем 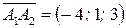 ,
, 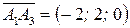 . Тогда векторное произведение векторов
. Тогда векторное произведение векторов  . Найдем модуль векторного произведения
. Найдем модуль векторного произведения 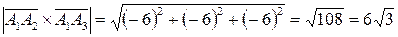 , а затем вычислим площадь треугольника
, а затем вычислим площадь треугольника 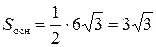 . Следовательно, высота, проведенная из вершины
. Следовательно, высота, проведенная из вершины  , будет равна
, будет равна 
Задача 5. Даны вершины треугольника  Найти внутренний угол при вершине
Найти внутренний угол при вершине  .
.
Решение. Угол 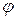 при вершине
при вершине  есть угол между векторами
есть угол между векторами  и
и  . Определим координаты этих векторов:
. Определим координаты этих векторов: 
 Найдем их модули:
Найдем их модули:


Из определения скалярного произведения следует, что косинус угла между векторами можно вычислить по формуле
 а угол при вершине треугольника
а угол при вершине треугольника 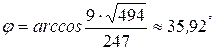 .
.
Задача 6. Вычислить площадь параллелограмма, построенного на векторах  и
и  , если
, если  ,
,  ,
, 

Решение. Найдем сначала векторное произведение векторов  и
и  , затем вычислим его модуль. Этот модуль численно равен площади параллелограмма, построенного на векторах
, затем вычислим его модуль. Этот модуль численно равен площади параллелограмма, построенного на векторах  и
и  .
.

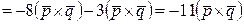 ;
; 
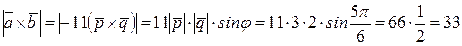 .
.
Следовательно, площадь параллелограмма 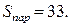
Задача 7. Разложить вектор 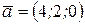 по базису, образованному векторами
по базису, образованному векторами 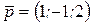 ,
,  ,
,  .
.
Решение. Разложить вектор  по векторам
по векторам 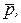
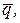
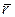 это значит представить его в виде линейной комбинации
это значит представить его в виде линейной комбинации  где
где  – искомые числа (постоянные величины). Сначала проверим, действительно ли векторы
– искомые числа (постоянные величины). Сначала проверим, действительно ли векторы 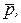
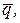
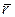 образуют базис. Для этого составим определитель третьего порядка из координат этих векторов и убедимся, что он отличен от нуля:
образуют базис. Для этого составим определитель третьего порядка из координат этих векторов и убедимся, что он отличен от нуля: 
Векторы 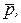
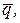
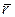 линейно-независимы. Представим линейную комбинацию в координатной форме
линейно-независимы. Представим линейную комбинацию в координатной форме  и составим систему линейных уравнений,
и составим систему линейных уравнений,  – неизвестные величины.
– неизвестные величины.

Решение полученной системы можно найти по формулам Крамера, методом Гаусса или с помощью обратной матрицы (см. задачи №1, 2). Данная система имеет решения:  Следовательно, разложение вектора
Следовательно, разложение вектора  имеет вид:
имеет вид: 
Задача 8.Даны вершины треугольника  . Найти уравнения прямых
. Найти уравнения прямых 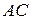 и
и 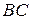 ; уравнение высоты, проведенной из точки
; уравнение высоты, проведенной из точки 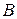 ; уравнение медианы, проведенной из вершины
; уравнение медианы, проведенной из вершины  .
.
Решение. Уравнения прямых 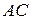 и
и 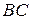 составим как уравнения прямых, проходящих через две точки.
составим как уравнения прямых, проходящих через две точки.
Уравнение прямой, проходящей через две точки  и
и  , имеет вид:
, имеет вид: 
 : Полагая
: Полагая  , получим
, получим  или
или  т.е.
т.е.  или
или  .
.
 :
:  , получим
, получим  или
или 
Уравнение высоты  , опущенной из вершины
, опущенной из вершины 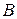 , составим как уравнение прямой, проходящей через точку
, составим как уравнение прямой, проходящей через точку 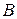 , перпендикулярно прямой
, перпендикулярно прямой 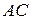 . Уравнение прямой, проходящей через данную точку в данном направлении, имеет вид:
. Уравнение прямой, проходящей через данную точку в данном направлении, имеет вид:  . Угловой коэффициент
. Угловой коэффициент  определим из условия перпендикулярности прямой
определим из условия перпендикулярности прямой 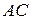 и высоты
и высоты  :
:  . Представим уравнение прямой
. Представим уравнение прямой 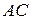 в виде
в виде  , из данной записи видно, что
, из данной записи видно, что  . Следовательно,
. Следовательно,  Координаты точки
Координаты точки 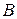 и полученный угловой коэффициент подставим в искомое уравнение:
и полученный угловой коэффициент подставим в искомое уравнение:  . Преобразуем данное уравнение
. Преобразуем данное уравнение  или
или 
Уравнение медианы, проведенной из вершины  , составим как уравнение прямой, проходящей через две точки: точку
, составим как уравнение прямой, проходящей через две точки: точку  и точку – середину стороны
и точку – середину стороны 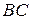 . Координаты середины отрезка можно найти по формулам:
. Координаты середины отрезка можно найти по формулам: 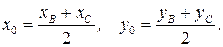 Обозначим середину отрезка
Обозначим середину отрезка 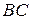 через точку
через точку 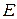 и найдем ее координаты:
и найдем ее координаты: 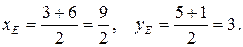
Таким образом, уравнение медианы  имеет вид
имеет вид  или
или  . После преобразований получим
. После преобразований получим  :
: 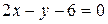 .
.
Задача 9. Определить какая кривая задана уравнением и указать ее основные параметры и построить:
а)  ; ; | в)  ; ; |
б)  ; ; | г)  . . |
Решение: Линии, определяемые алгебраическими уравнениями второй степени относительно  т.е.
т.е.  (коэффициенты
(коэффициенты  одновременно не равны нулю), называются кривыми второго порядка. Каждое из заданных уравнений не содержит члена с произведением разноименных координат, следовательно, оно может определять окружность, либо эллипс, либо гиперболу, либо параболу с осями симметрии, параллельными осям координат.
одновременно не равны нулю), называются кривыми второго порядка. Каждое из заданных уравнений не содержит члена с произведением разноименных координат, следовательно, оно может определять окружность, либо эллипс, либо гиперболу, либо параболу с осями симметрии, параллельными осям координат.
а)  . Выделим полные квадраты по каждой из переменных и преобразуем уравнение к простейшему виду:
. Выделим полные квадраты по каждой из переменных и преобразуем уравнение к простейшему виду:
| |


Уравнение задает окружность с центром в точке  и
и  (рис.1).
(рис.1).
 |
Рис.1.
б)  . Преобразуем уравнение
. Преобразуем уравнение
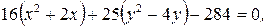

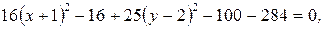

 Уравнение – эллипс с центром в точке
Уравнение – эллипс с центром в точке  , полуоси:
, полуоси:  (рис.2).
(рис.2).
Рис.2.
в)  . В левой части уравнения выделим формулу полного квадрата и приведем к каноническому виду:
. В левой части уравнения выделим формулу полного квадрата и приведем к каноническому виду:

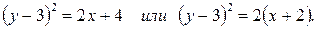
Уравнение определяет параболу с вершиной в точке  , осью симметрии
, осью симметрии  , ветви в положительном направлении оси
, ветви в положительном направлении оси  . Точки пересечения с
. Точки пересечения с  :
:  , тогда
, тогда  ; отсюда
; отсюда  (рис.3).
(рис.3).
 |
Рис.3.
г) Заданное уравнение  преобразуем
преобразуем

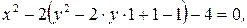


|
 и полуосями
и полуосями  ,
,  (рис.4).
(рис.4). 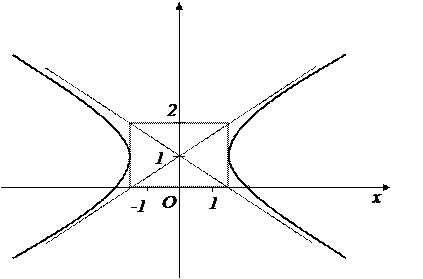 |
Рис.4.
Задача 10.Составить уравнение плоскости, проходящей через точку 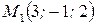 перпендикулярно вектору
перпендикулярно вектору  , если
, если 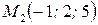 .
.
Решение. Искомое уравнение плоскости имеет вид:  , где
, где  – координаты вектора
– координаты вектора 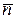 , перпендикулярного данной плоскости.
, перпендикулярного данной плоскости.
Вектор  имеет координаты
имеет координаты 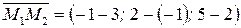 или
или  Так как плоскость перпендикулярна вектору
Так как плоскость перпендикулярна вектору  , то значения параметров
, то значения параметров  и
и  равны
равны  соответственно. Уравнение плоскости, таким образом, имеет вид
соответственно. Уравнение плоскости, таким образом, имеет вид  Точка
Точка 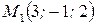 по условию задачи лежит в плоскости. Следовательно, подстановкой координат точки
по условию задачи лежит в плоскости. Следовательно, подстановкой координат точки  в уравнение плоскости получим:
в уравнение плоскости получим:

Отсюда находим, что  Уравнение искомой плоскости:
Уравнение искомой плоскости:
 или
или 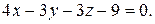
Задача 11. Найти величину угла между плоскостями:
1)  и
и 
2)  и
и 
Решение. Углом между двумя плоскостями называется угол между нормальными векторами этих плоскостей. Если две плоскости заданы уравнениями  и
и  то величина угла
то величина угла 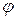 между ними вычисляется по формуле:
между ними вычисляется по формуле:

Величина наименьшего из двух смежных углов, образованных этими плоскостями, находится по формуле:
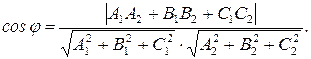
1) Воспользуемся формулой для нахождения острого угла между плоскостями и подставим в нее значения коэффициентов
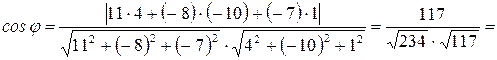

Отсюда следует, что угол между плоскостями 
2)В данном задании можно заметить, что выполняется условие перпендикулярности плоскостей  :
:  . Следовательно, плоскости взаимно перпендикулярны;
. Следовательно, плоскости взаимно перпендикулярны; 
Задача 12.Даны комплексные числа 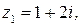

 . Требуется:
. Требуется:
1) вычислить  ;
;
2) вычислить  и сделать проверку;
и сделать проверку;
3) найти модуль и аргумент числа  с точностью до
с точностью до  записать это число в тригонометрической и показательной формах;
записать это число в тригонометрической и показательной формах;
4) найти все значения корня 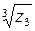 ;
;
5) решить уравнение  .
.
Решение. Заданы комплексные числа в алгебраической форме 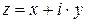 , где
, где  – действительные числа,
– действительные числа,  – мнимая единица,
– мнимая единица,  ;
;  .
.
1) Произведением комплексных чисел  и
и  называется комплексное число, определяемое равенством
называется комплексное число, определяемое равенством

Например,  .
.
Два комплексных числа 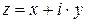 и
и 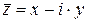 , отличающиеся лишь знаком мнимой части, называются сопряженными. Если задано число
, отличающиеся лишь знаком мнимой части, называются сопряженными. Если задано число  , то сопряженное число
, то сопряженное число  . Найдем произведение
. Найдем произведение
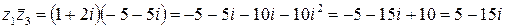 .
.
2) Частным двух комплексных чисел  и
и  называется комплексное число
называется комплексное число  , которое, будучи умноженным на
, которое, будучи умноженным на  , дает число
, дает число  .
.

На практике частное двух комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю («избавляются от мнимости в знаменателе»).
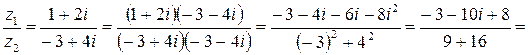

Сделаем проверку, найдя произведение

Таким образом, частное  вычислено правильно.
вычислено правильно.
3) Тригонометрическая форма комплексного числа  ; показательная форма
; показательная форма 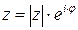 , где
, где  – модуль, угол
– модуль, угол 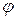 – аргумент комплексного числа.
– аргумент комплексного числа.
Аргумент 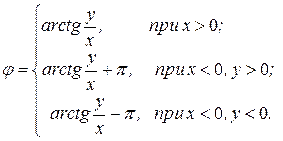
Представим число 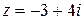 в тригонометрической и показательной формах. Найдем модуль и аргумент заданного числа с точностью до
в тригонометрической и показательной формах. Найдем модуль и аргумент заданного числа с точностью до 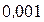 :
:



 Таким образом,
Таким образом,  – тригонометрическая форма заданного комплексного числа;
– тригонометрическая форма заданного комплексного числа; 
4) Корень 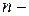 ой степени из комплексного числа имеет
ой степени из комплексного числа имеет  различных значений, которые находят по формуле
различных значений, которые находят по формуле
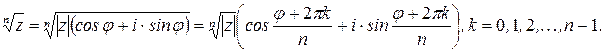 Число
Число 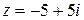 представим в тригонометрической форме:
представим в тригонометрической форме: 

 – тригонометрическая форма.
– тригонометрическая форма.
По формуле находим
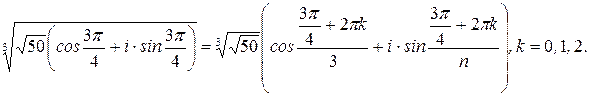
Полагая 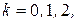 получим
получим
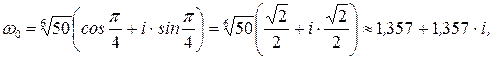



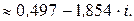
Найденным значениям корня соответствуют вершины правильного треугольника, вписанного в окружность радиуса  с центром в начале координат.
с центром в начале координат.
5)Решить уравнение  , если
, если  .
.
Найдем модуль комплексного числа  и возведем его в квадрат:
и возведем его в квадрат: 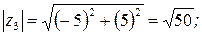
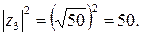 Подставим число 50 в заданное уравнение и получим квадратное уравнение
Подставим число 50 в заданное уравнение и получим квадратное уравнение 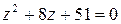 .
.
Известно, что квадратное уравнение 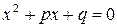 , где
, где  – действительные числа, имеет действительное решение только в случае, если дискриминант
– действительные числа, имеет действительное решение только в случае, если дискриминант  этого уравнения неотрицателен. Если дискриминант
этого уравнения неотрицателен. Если дискриминант  , то действительных решений нет. Причина отсутствия корней заключается в невозможности, оставаясь в рамках действительных чисел, извлечь корень из отрицательного числа. Однако можно найти комплексные значения корня из отрицательного числа. Поэтому уравнение
, то действительных решений нет. Причина отсутствия корней заключается в невозможности, оставаясь в рамках действительных чисел, извлечь корень из отрицательного числа. Однако можно найти комплексные значения корня из отрицательного числа. Поэтому уравнение  имеет два комплексных корня и в случае отрицательного дискриминанта. Найти эти корни можно с помощью формулы для корней квадратного уравнения.
имеет два комплексных корня и в случае отрицательного дискриминанта. Найти эти корни можно с помощью формулы для корней квадратного уравнения.
Решим уравнение 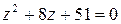 . Вычислим корни уравнения по формуле
. Вычислим корни уравнения по формуле  . Найдем
. Найдем 
 . Согласно формулам для корней квадратного уравнения получим
. Согласно формулам для корней квадратного уравнения получим 
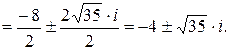
Таким образом, 
 – корни исходного квадратного уравнения.
– корни исходного квадратного уравнения.
Задача 13.Решить уравнение  .
.
Решение. Уравнение третьей степени  , где
, где  – любые числовые коэффициенты, решают с помощью замены
– любые числовые коэффициенты, решают с помощью замены  .
.
В таком случае  , а
, а 
 . Заменяя
. Заменяя  новым неизвестным
новым неизвестным 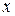 , мы получим уравнение относительно неизвестного
, мы получим уравнение относительно неизвестного 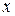 , не содержащего квадрата этого неизвестного, т.е. уравнение вида
, не содержащего квадрата этого неизвестного, т.е. уравнение вида  .
.
Одним из способов решения подобного уравнения третьей степени – это применение формулы Кардана: 

 где
где 

 и
и  – корни уравнения
– корни уравнения  , т.е.
, т.е. 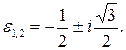
В заданном уравнении  ; сделаем замену
; сделаем замену  . Получим
. Получим 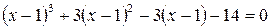 или
или  . Уравнение приведено к виду
. Уравнение приведено к виду  , т.е.
, т.е.  . Найдем
. Найдем  по формулам:
по формулам:
 ;
; 
Таким образом,  ;
;
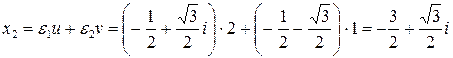 ;
;
 .
.
Сделаем обратную замену  . Значит корни исходного уравнения:
. Значит корни исходного уравнения:  ,
,  ,
, 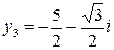 .
.
Для проверки необходимо воспользоваться свойствами корней кубического уравнения:  ;
; 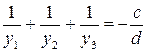 ;
;  .
.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Бугров Н. С., Никольский С. М. Элементы линейной алгебры и аналитической геометрии. –М. : Наука, 1988.
2. Данко П. Е., Попов А. Г., Кожевникова Т. Н. Высшая математика в упражнениях и задачах. Часть 1. –М.: Высшая школа, 1986.
3. Игнатьева А.В., Краснощекова Т.И., Смирнов В.Ф. Курс высшей математики. – М.: Высшая школа, 1968.
4. Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты): Учеб. Пособие для втузов. – М.: Высш. школа, 1983.
5. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1986.
6. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 1 курс. – 3-е изд., испр. и доп. – М.: Айрис-пресс, 2003.
7. Письменный Д.Т. Конспект лекций по высшей математике. 1 часть. – 2-е изд., – М.: Айрис-пресс, 2003.
