Каноническое уравнение прямой в пространстве

Если известны координаты точки A(x₀, y₀, z₀) лежащей на прямой и направляющего вектора

n = {l; m; n}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу

x -x0	=	y -y0	=	z -z0
l	m	n

29.

Взаимное расположение прямой и плоскости в пространстве.

Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.

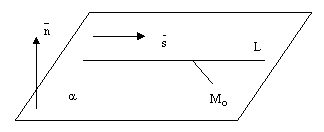
рис.6.

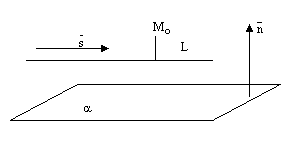
рис.7.

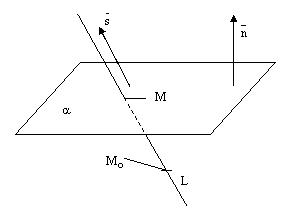
рис.8.

Теорема. Пусть плоскость 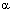задана общим уравнением

,

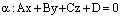а прямая L задана каноническими уравнениями

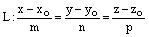
или параметрическими уравнениями

, ,

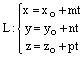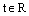в которых 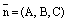– координаты нормального вектора плоскости 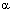, 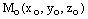– координаты произвольной фиксированной точки прямой L, –

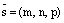координаты направляющего вектора прямой L. Тогда:

1) если 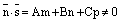, то прямая L пересекает плоскость 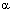в точке,координаты которой 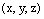можно найти из системы уравнений

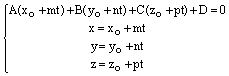; (7)

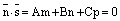2) если и 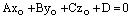, то прямая лежит на плоскости;

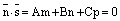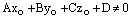3) если и , то прямая параллельна плоскости.

Доказательство. Условие 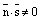говорит о том, что вектроры 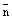и 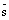не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит пересекает ее в некоторой точке М. Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальныеуравнения системы, находим координаты искомой точки.

Если 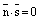, то это означает, что 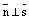. А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости икоординаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка 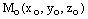. Если 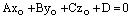, то точка 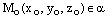– лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.

Если 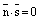, а 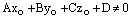, то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.

Теорема доказана.

31.

Понятие функции

Назовем упорядоченной парой (x, y) двухэлементное множество {x, y}, в

котором элемент x находится на первом месте, а элемент y – на втором.

Элемент x называется первой координатой упорядоченной пары, а элемент y –

второй координатой. Две упорядоченные пары равны, когда совпадают их

координаты: (x, y)  (u,v) x  u, y  v .

Функцией f называется множество упорядоченных пар чисел (x, y) , таких,

что x X , y Y и каждому элементу x X ставится в соответствие

единственный элемент y Y . Обозначение: f: X → Y. Множество X называется

областью определения функции f, а множество Y – областью значений.

Обозначают: Df и Ef. Если ясно, какие множества X и Y имеются в виду, то

пишут y  f (x) . Элемент x называется аргументом, а y – значением функции f.