Основные методы интегрирования
Учреждение образования «Белорусская государственная
Сельскохозяйственная академия»
Кафедра высшей математики
НЕОПРЕДЕЛЁННЫЙ И ОПРЕДЕЛЁННЫЙ
ИНТЕГРАЛЫ
Конспект лекции для студентов бухгалтерского факультета
заочной формы получения образования (НИСПО)
Горки, 2013
Неопределённый и определённый интегралы
Первообразная функция и неопределённый интеграл
В дифференциальном исчислении решается задача нахождения производной или дифференциала данной функции. Пусть дана функция 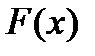 . Тогда по определению производной
. Тогда по определению производной 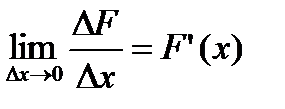 . Обозначим
. Обозначим 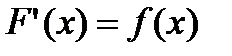 .
.
В интегральном исчислении решается задача, обратная задаче нахождения производной: отыскание функции 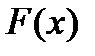 по заданной её производной
по заданной её производной 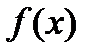 . Таким образом, для заданной функции
. Таким образом, для заданной функции 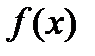 нужно найти такую функцию
нужно найти такую функцию 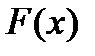 , чтобы
, чтобы 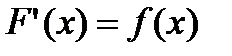 .
.
Функция 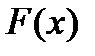 называется первообразной функцией для функции
называется первообразной функцией для функции 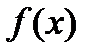 на некотором множестве D, если на этом множестве
на некотором множестве D, если на этом множестве 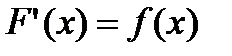 .
.
Если 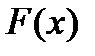 есть первообразная функция для функции
есть первообразная функция для функции 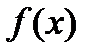 , то каждая из функций
, то каждая из функций 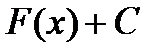 , где C - произвольная постоянная, будет также первообразной для функции
, где C - произвольная постоянная, будет также первообразной для функции 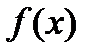 , так как
, так как
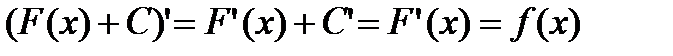 .
.
Таким образом, если функция 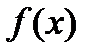 имеет хотя бы одну первообразную функцию, то она может иметь бесчисленное множество первообразных функций и все они отличаются одна от другой на постоянную величину.
имеет хотя бы одну первообразную функцию, то она может иметь бесчисленное множество первообразных функций и все они отличаются одна от другой на постоянную величину.
Совокупность всех первообразных функций F(x)+C для функции f(x) называется неопределённым интегралом от функции f(x) и обозначается 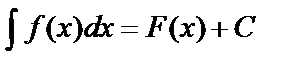 . Процесс нахождения первообразной функции называется интегрированием. Переменная х называется переменной интегрирования, функция f(x) называется подынтегральной функцией, выражение f(x)dx – подынтегральным выражением.
. Процесс нахождения первообразной функции называется интегрированием. Переменная х называется переменной интегрирования, функция f(x) называется подынтегральной функцией, выражение f(x)dx – подынтегральным выражением.
Неопределённый интеграл обладает свойствами, использование которых в значительной степени может упростить интегрирование функций.
 Производная от неопределённого интеграла равна подынтегральной функции, т.е.
Производная от неопределённого интеграла равна подынтегральной функции, т.е. 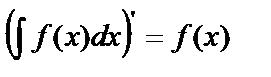 .
.
 Дифференциал неопределённого интеграла равен подынтегральному выражению, т.е.
Дифференциал неопределённого интеграла равен подынтегральному выражению, т.е. 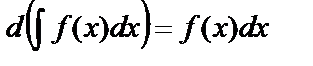 .
.
 Неопределённый интеграл от дифференциала функции равен этой функции плюс произвольная постоянная, т.е.
Неопределённый интеграл от дифференциала функции равен этой функции плюс произвольная постоянная, т.е. 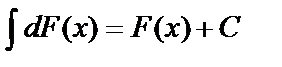 .
.
 Постоянный множитель можно выносить за знак интеграла:
Постоянный множитель можно выносить за знак интеграла: 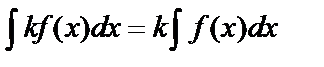 .
.
 Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций, т.е.
Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций, т.е. 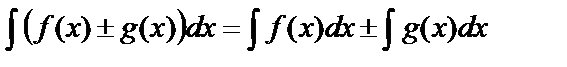 .
.
 Результат интегрирования не зависит от обозначения переменной интегрирования, т.е. если
Результат интегрирования не зависит от обозначения переменной интегрирования, т.е. если 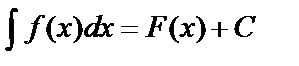 , то при замене переменной интегрирования х на t
, то при замене переменной интегрирования х на t 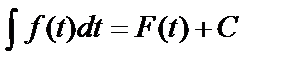 . Такое свойство называется инвариантностью формулы интегрирования.
. Такое свойство называется инвариантностью формулы интегрирования.
Таблица основных интегралов
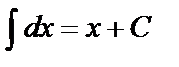 | 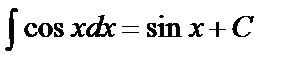 | ||
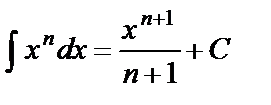 | 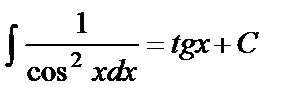 | ||
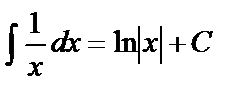 | 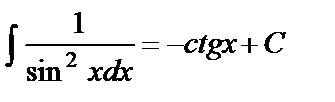 | ||
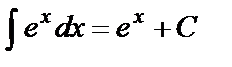 | 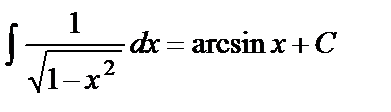 | ||
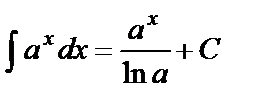 | 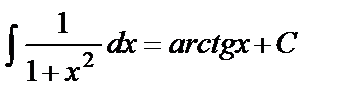 | ||
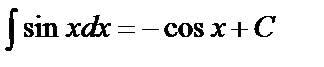 |
Интегралы данной таблицы называются табличными. Каждая из формул таблицы справедлива в области определения подынтегральной функции.
Основные методы интегрирования
При интегрировании функций не всегда можно сразу использовать таблицу интегралов. Как правило, вначале нужно данный интеграл преобразовать таким образом, чтобы свести его к одной или нескольким формулам таблицы. Для этого используются специальные методы интегрирования, основными из которых являются непосредственное интегрирование, замена переменной (или метод подстановки), метод интегрирования по частям.
Суть метода непосредственного интегрирования состоит в том, что данный интеграл с помощью алгебраических преобразований и свойств неопределённого интеграла сводится к табличным интегралам.
Примеры 1 –3. Найти неопределённые интегралы:
а) 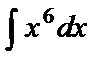 ; б)
; б) 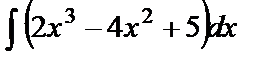 ; в)
; в) 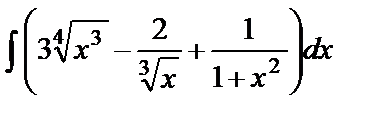 .
.
Решение. а) 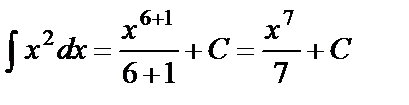 ;
;
б) 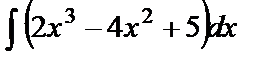 =
= 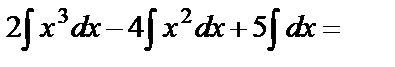
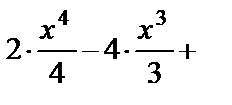
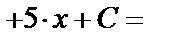
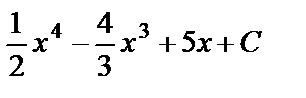 ;
;
в) 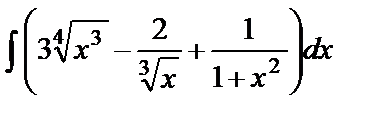 =
= 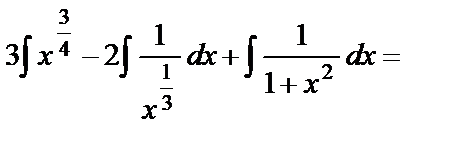
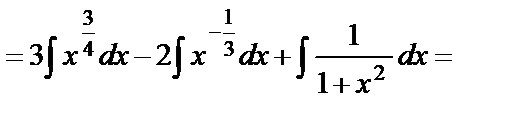
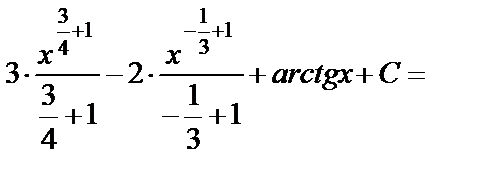
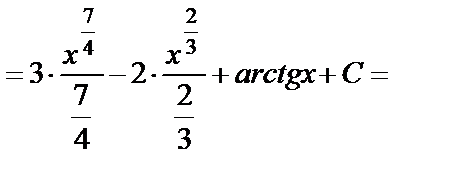
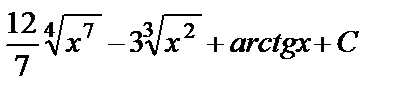 .
.
Если интеграл непосредственно не находится, то во многих случаях результат может быть достигнут с помощью метода замены переменной (подстановки). Данный метод помогает значительно упростить подынтегральное выражение и свести интеграл к одной из формул таблицы.
Если подынтегральная функция представляет собой дробь, у которой числитель есть производная знаменателя, то такой интеграл равен логарифму натуральному от абсолютной величины знаменателя, т.е. 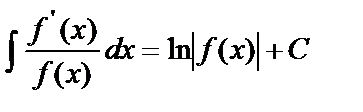 .
.
Примеры 4 – 7. Найти интегралы: а) 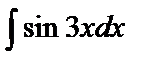 ; б)
; б) 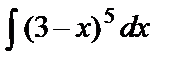 ; в)
; в) 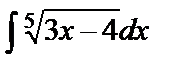 ; г)
; г) 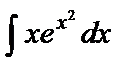 .
.
Решение. а) 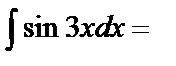 {заменим u=3x, тогда du=3dx,
{заменим u=3x, тогда du=3dx, 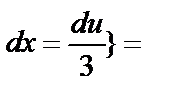
= 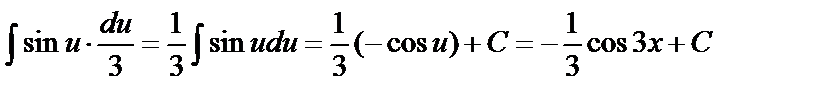 ;
;
б) 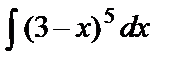 ={заменим u=3
={заменим u=3  x, du=
x, du=  dx, dx=
dx, dx=  du}=
du}= 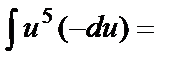
= 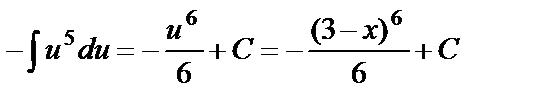 ;
;
в) 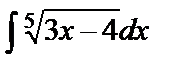 ={u=3x
={u=3x  4, du=3dx,
4, du=3dx, 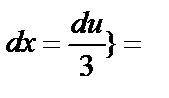
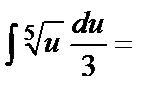
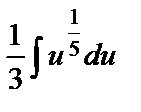 =
=
= 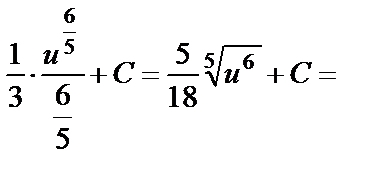
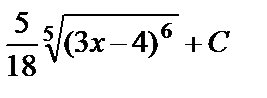 ;
;
г) 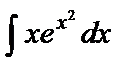 ={
={ 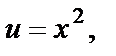 du=2xdx,
du=2xdx, 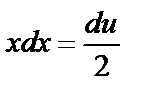 }=
}= 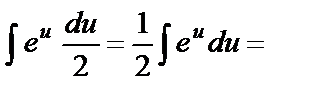
= 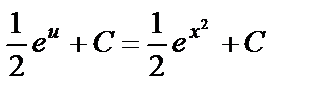 .
.
Для нахождения интеграла вида 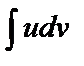 используется формула интегрирования по частям
используется формула интегрирования по частям 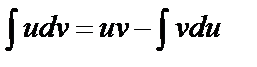 . Если в результате получилось, что интеграл в правой части формулы проще, чем в левой, то применение этой формулы оправдано. Обычно в подынтегральном выражении за функцию u принимают тот множитель, который после его дифференцирования становится более простым. Оставшуюся часть подынтегрального выражения принимают за дифференциал dv некоторой функции v.
. Если в результате получилось, что интеграл в правой части формулы проще, чем в левой, то применение этой формулы оправдано. Обычно в подынтегральном выражении за функцию u принимают тот множитель, который после его дифференцирования становится более простым. Оставшуюся часть подынтегрального выражения принимают за дифференциал dv некоторой функции v.
При использовании данного метода интегрирования удобно пользоваться следующими рекомендациями:
 в интегралах вида
в интегралах вида 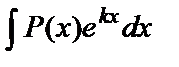 ,
, 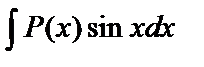 ,
, 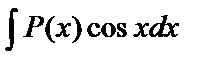 имеет смысл положить u=P(x), а в качестве dv взять оставшуюся часть подынтегрального выражения;
имеет смысл положить u=P(x), а в качестве dv взять оставшуюся часть подынтегрального выражения;
 в интегралах вида
в интегралах вида 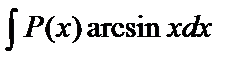 ,
, 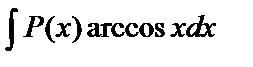 ,
, 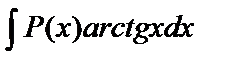 ,
, 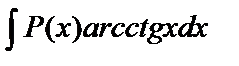 ,
, 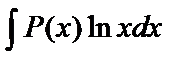 следует положить dv=P(x)dx, а оставшуюся часть подынтегрального выражения обозначить через u;
следует положить dv=P(x)dx, а оставшуюся часть подынтегрального выражения обозначить через u;
 в интегралах вида
в интегралах вида 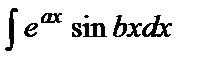 ,
, 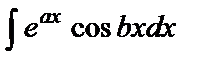 можно положить
можно положить 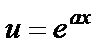 , а оставшуюся часть подынтегрального выражения принять за dv.
, а оставшуюся часть подынтегрального выражения принять за dv.
Примеры 8 – 9. Найти интегралы: а) 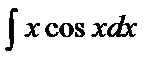 ; б)
; б) 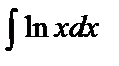 .
.
Решение. а) 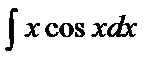 =
= 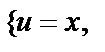
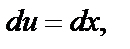
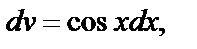
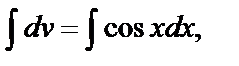
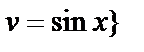 =
= 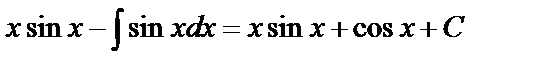 ;
;
б) 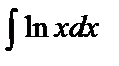 =
= 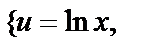
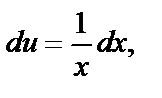
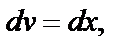
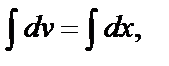
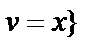 =
=
= 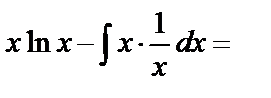
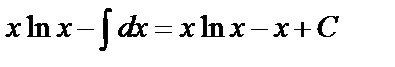 .
.
