Свойства неопределенного интеграла

ГЛАВА 6

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Первообразная функция

Основной задачей дифференциального исчисления является нахождение производной от данной функции. Интегральное исчисление решает обратную задачу: найти функцию F(x), зная ее производную . Искомую функцию называют первообразной функции .

Определение.

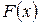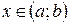Функция называется первообразной функции на интервале , если для любого выполняется равенство:

.

Примеры

1. Функция 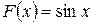является первообразной для функции при любом х, так как .

2. Функция 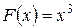есть первообразная для функции 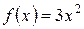на всей числовой оси, ибо .

Нетрудно заметить, что любая функция вида 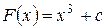, где с − постоянная, также является первообразной для функции 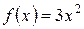, поскольку .

Приведем теорему, выражающую основное свойство первообразной.

Теорема.

Если функция 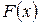является первообразной функции на интервале , то множество всех первообразных для задается формулой

,

где с − постоянное число.

Таким образом, множество функций представляет собой семейство всех первообразных для данной функции .

Неопределенный интеграл

Определение.

Совокупность всех первообразных функций для данной функции на интервале называется неопределенным интегралом.

Обозначается:

,

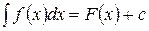где − подынтегральная функция,

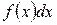− подынтегральное выражение.

Операция нахождения первообразной для данной функции называется интегрированием этой функции.

Дифференцирование и интегрирование функций − это две взаимно обратные операции.

Определение.

График какой-либо первообразной 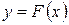функции называется интегральной кривой.

Геометрически неопределенный интеграл представляет собой семейство параллельных кривых , в котором каждому числовому значению с соответствует определенная кривая (рис.6.1).

Рис. 6.1

Условие существования первообразной или неопределенного интеграла сформулировано в следующей теореме.

Теорема.

Если функция непрерывна на интервале , то имеет на этом интервале первообразную, а следовательно, и неопределенный интеграл.

Замечание.

Если функция имеет точки разрыва, то ее можно интегрировать на каждом промежутке непрерывности раздельно.

Свойства неопределенного интеграла

Отметим ряд свойств неопределенного интеграла, вытекающих из его определения.

1. Дифференциал от неопределенного интеграла равен подынтегральному выражению:

.

2. Производная неопределенного интеграла равна подынтегральной функции:

.

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

.

4. Постоянный множитель можно выносить за знак интеграла:

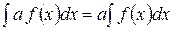, а − постоянная.

5. Неопределенный интеграл от суммы (разности) функций равен сумме (разности) их неопределенных интегралов:

.

6. Всякая формула интегрирования сохраняет свой вид при подстановке вместо независимой переменной любой дифференцируемой от нее функции.

Если 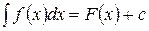, то и , где .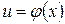

Таблица основных интегралов

Для облегчения интегрирования (нахождения первообразных) существует таблица основных интегралов, которая получена из основных формул дифференциального исчисления (таблицы дифференциалов) и использования свойств неопределенного интеграла.

В таблице переменная интегрирования u может обозначать как независимую переменную, так и функцию от независимой переменной: 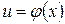(п.6.3).

1.	;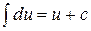
2.	;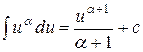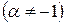
3.	;
4.	;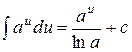
5.	;
6.	;
7.	;
8.	;
9.	;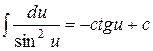
10.	;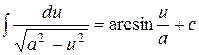
11.	;
12.	;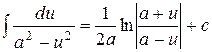
13.	;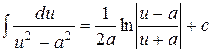
14.	.

Справедливость указанных формул проверяется дифференцированием.

Методы интегрирования

Интегрирование является значительно более сложным действием, чем дифференцирование, поскольку для отыскания первообразных нет таких универсальных правил и формул, как в дифференциальном исчислении.

Методы интегрирования сводятся к указанию ряда приемов, приводящих данный интеграл к табличному. К наиболее важным методам интегрирования относятся: непосредственное интегрирование, замена переменной (метод подстановки) и интегрирование по частям.