Теория потенциалов, определение, основные свойства
Пусть в точке 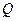 расположен заряд величины
расположен заряд величины 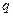 , тогда в любой точке
, тогда в любой точке 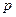 пространства будет создаваться поле, потенциал которого:
пространства будет создаваться поле, потенциал которого: 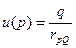 . Для системы зарядов, потенциал имеет вид:
. Для системы зарядов, потенциал имеет вид: 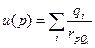 .
.
 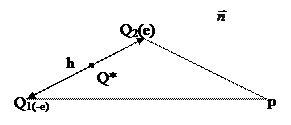 | Диполь: Пусть в точках 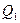 и и 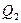 расположены заряды, величиной –e и +e. расположены заряды, величиной –e и +e. 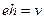 - момент диполя, будем сближать точки - момент диполя, будем сближать точки 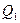 и и 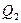 , сохраняя величину , сохраняя величину 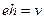 (увеличивая e), то в пределе при (увеличивая e), то в пределе при 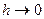 получим точечный диполь, расположенный в точке Q, потенциал которого равен: получим точечный диполь, расположенный в точке Q, потенциал которого равен: 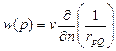 . . |
Рассмотрим интеграл: 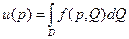 ,
, 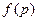 - интегрируема (непрерывна) везде, кроме
- интегрируема (непрерывна) везде, кроме 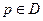 , если
, если 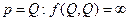 . Рассмотрим его сходимость и непрерывность.
. Рассмотрим его сходимость и непрерывность.
Определение: будем говорить, что это интеграл сходиться равномерно в окрестности точки 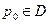 , если для любого
, если для любого 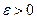 существует такое
существует такое 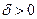 , (
, ( 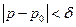 ), что для любой точки
), что для любой точки 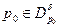 , (
, ( 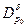 - окрестность т.
- окрестность т. 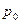 ,
, 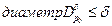 ) выполняется :
) выполняется : 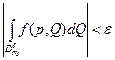 .
.
Теорема: если 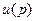 сходится равномерно в окрестности точки
сходится равномерно в окрестности точки 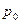 , то
, то 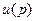 существует и непрерывна в точке
существует и непрерывна в точке 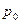 .
.
Доказательство: разобьём 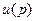 на 2 функции:
на 2 функции: 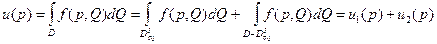 , рассмотрим разность:
, рассмотрим разность: 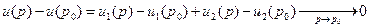 (она мала, если
(она мала, если 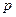 и
и 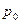 близки).
близки).
Докажем более подробно. Поскольку 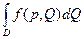 сходится в окрестности
сходится в окрестности 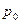 , то берём
, то берём 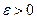 и выбираем такое
и выбираем такое 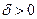 , что
, что 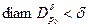 и
и 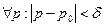 , тогда выполняется
, тогда выполняется 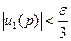 и
и 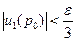 . Так как
. Так как 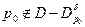 , то интеграл
, то интеграл 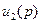 не является не собственным, и
не является не собственным, и 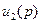 непрерывна в точке
непрерывна в точке 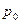 . Значит, для того же
. Значит, для того же 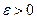 существует такое
существует такое 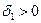 , что
, что 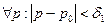 выполняется
выполняется 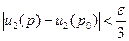 . Пусть
. Пусть 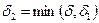 , тогда
, тогда 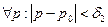 выполняется
выполняется 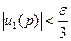 ,
, 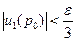 и
и 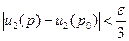 , а следовательно и
, а следовательно и 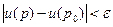 .
.
Чтд.
Замечание: из равномерной сходимости следует сходимость интеграла.
При определении интеграла предполагалось, что промежуток интегрирования конечен и подынтегральная функция определена и непрерывна на этом промежутке. Такой интеграл называется собственным. Если нарушается хотя бы одно из этих условий, то интеграл называется несобственным.
A) Объёмный потенциал
Потенциал поля, созданного зарядами, распределёнными в области 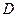 с плотностью
с плотностью 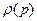 , равен
, равен 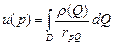 и называется объёмным потенциалом.
и называется объёмным потенциалом.
Свойство 1. Объёмный потенциал определён и непрерывен всюду.
Если 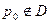 , то интеграл
, то интеграл 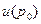 не является не собственным. Поскольку подынтегральная функция, как функция
не является не собственным. Поскольку подынтегральная функция, как функция 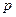 , непрерывна в точке
, непрерывна в точке 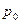 , то непрерывен в этой точке и интеграл
, то непрерывен в этой точке и интеграл 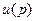 .
.
Если 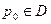 , то, согласно теореме и замечанию, достаточно доказать равномерную сходимость, интеграла в окрестности точки
, то, согласно теореме и замечанию, достаточно доказать равномерную сходимость, интеграла в окрестности точки 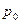 . Для этого оценим интеграл:
. Для этого оценим интеграл: 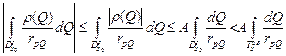 , мы увеличили область, поместив всё в шар
, мы увеличили область, поместив всё в шар 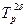 , радиуса
, радиуса 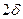 . Перейдём в последнем интеграле к сферическим координатам и получим тогда:
. Перейдём в последнем интеграле к сферическим координатам и получим тогда: 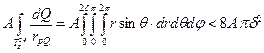 , чтобы интеграл был меньше заданного
, чтобы интеграл был меньше заданного 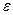 , достаточно взять
, достаточно взять 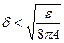 .
.
Свойство 2. Объёмный потенциал имеет всюду непрерывные частные производные первого порядка по координатам точки 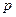 .
.
Если 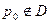 , то интеграл
, то интеграл 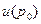 не является не собственным. Поскольку подынтегральная функция, как функция точки
не является не собственным. Поскольку подынтегральная функция, как функция точки 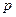 , имеет в точке
, имеет в точке 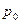 непрерывные частные производные первого порядка по координатам точки
непрерывные частные производные первого порядка по координатам точки 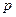 , то этим свойством обладает и интеграл
, то этим свойством обладает и интеграл 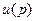 , причём производные вычисляются путём дифференцирования под знаком интеграла:
, причём производные вычисляются путём дифференцирования под знаком интеграла: 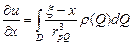 ,
, 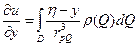 ,
, 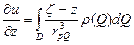 - (1), где
- (1), где 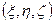 - координаты точки
- координаты точки 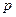 .
.
Если 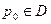 , то, согласно теореме и замечанию, достаточно доказать равномерную сходимость в окрестностях точки
, то, согласно теореме и замечанию, достаточно доказать равномерную сходимость в окрестностях точки 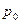 интегралов от производных в правых частях формул. Тогда законно дифференцирование под знаком интеграла, причём для производных
интегралов от производных в правых частях формул. Тогда законно дифференцирование под знаком интеграла, причём для производных 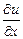 ,
, 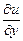 и
и 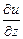 справедливы формулы (1). Для определённости рассмотрим интеграл:
справедливы формулы (1). Для определённости рассмотрим интеграл: 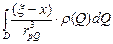 . Оценим его:
. Оценим его: 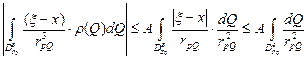 , т.к.
, т.к. 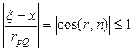 .
.
Далее, 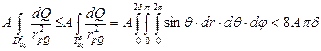 , достаточно взять
, достаточно взять 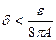 для того, чтобы выполнялось неравенство
для того, чтобы выполнялось неравенство 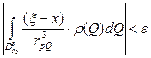 .
.
Свойство 3. Объёмный потенциал является гармонической функцией вне области 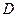 , в которой расположены заряды (массы). Это свойство следует из того, что для точек
, в которой расположены заряды (массы). Это свойство следует из того, что для точек 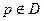 интеграл
интеграл 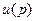 не является не собственным, и поэтому оператор Лапласа можно вносить под знак интеграла:
не является не собственным, и поэтому оператор Лапласа можно вносить под знак интеграла:
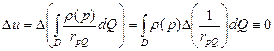 , т.к. для точек
, т.к. для точек 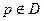 (а точнее P≠Q) имеем
(а точнее P≠Q) имеем 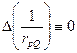 .
.
Свойство 4. в точках области 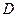 объёмный потенциал удовлетворяет соотношению:
объёмный потенциал удовлетворяет соотношению: 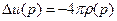 , т.к.
, т.к. 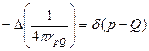 ,
, 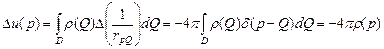 .
.
Вторые производные рвутся.
Свойство 5. При стремлении точки наблюдения к бесконечности объёмный потенциал стремится к нулю ( 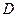 - огр.).
- огр.).
Применим теорему о среднем: 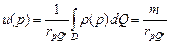 , где
, где 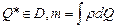 - суммарный заряд. Т.о.
- суммарный заряд. Т.о. 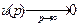 .
.
