Основные требования к курсовой работе

Методические указания

к выполнению курсовой работы по дисциплине

"Информатика"

на тему «Исследование траектории полета ЛА»

Направление подготовки: 160100 «Авиа- и ракетостроение»

Специальности подготовки:160302 «Ракетные двигатели»

160801 «Ракетостроение»

160701 «Баллистика»

Тула 2008 г.

Разработал: Фомичева О.А, к.т н., ассистент.

Методические указания для курсовой работы обсуждены на заседании кафедры ракетостроения

" ____"______________2008 г.

Заведующий кафедрой ______________________ В.В. Ветров

Нормоконтролер,

ответственный за стандартизацию на кафедре

___________________ С.И. Стреляев

СОДЕРЖАНИЕ

ВВЕДЕНИЕ..................................................................................................... 4

1. Цель курсовой работы................................................................... 4

2. ОСНОВЫ ТЕОРИИ................................................................................... 5

2.1. Физическая модель полета ЛА.............................................................. 5

2.2. Математическая модель траектории полета ЛА.................................. 6

2.3. Численная модель траектории полета ЛА............................................ 6

3. ОСНОВНЫЕ ТРЕБОВАНИЯ К КУРСОВОЙ РАБОТЕ.......................... 8

3.1. Задание на курсовую работу................................................................ 8

3.2. Содержание пояснительной записки.................................................... 8

3.3. Оформление пояснительной записки.................................................... 8

4. ПОРЯДОК ВЫПОЛНЕНИЯ КУРСОВОЙ РАБОТЫ.............................. 9

5. ПРЕДСТАВЛЕНИЕ РАБОТЫ К ЗАЩИТЕ............................................. 9

Библиографический список.......................................................... 10

Приложение 1................................................................................................ 11

ВВЕДЕНИЕ

Важнейшей особенностью современного этапа научно технического прогресса является стремительно возрастающая роль ЭВМ во всех областях инженерной деятельности - от систем автоматизированного проектирования и управления до контроля технологическими процессами. В настоящее время ЭВМ стали необходимым оборудованием НИИ, конструкторских бюро, заводов. Это позволило от простейших расчетов и оценок различных конструкций или процессов перейти к новому уровню инженерной деятельности - детальному математическому моделированию (вычислительному эксперименту), которое существенно сокращает потребность в натурных экспериментах, а в ряде случаев может их заменить. В связи с этим современный специалист с высшим образованием должен обладать не только высоким уровнем подготовки по профилю своей специальности, но и хорошо знать математические методы решения инженерных задач, ориентироваться на использование вычислительной техники, практически освоить принципы работы на ЭВМ.

Цель курсовой работы

Целью данной курсовой работы является выработка у студентов навыки активного применения ЭВМ в современных информационных процессах, изучения технических и программных средств реализации информационных процессов, при проектировании и исследовании современных изделий и технологий, овладения основными методами постановки задач проектирования ЛА с помощью ЭВМ, проведение вычислительных экспериментов, принятие решений и отображения результатов, усвоение основных принципов и методик использования и создания современных вычислительных комплексов. повышение уровня фундаментальной подготовки в области вычислительных методов и программирования, развития у студентов логического и алгоритмического мышления.

У студента вырабатывается ориентация на решение проблем проектирования ЛА с помощью ЭВМ, навыки использования ЭВМ при решении прикладных задач.

Студент должен уметь правильно и рационально выбрать метод решения задачи, составить алгоритм ее решения с учетом особенностей конкретной задачи и возможностей имеющихся в его распоряжении ЭВМ, составить алгоритм и программу на алгоритмическом языке программирования, отладить ее и правильно интерпретировать полученные результаты. Для этого необходимо знание основ устройства ЭВМ и вычислительных систем, технических и программных средств реализации информационных процессов, алгоритмических языков программирования, численных методов решения математических задач, баз данных, компьютерной графики.

Выполнение курсовой работы направлено на овладение практическими навыками использования ЭВМ для численного решения обыкновенных дифференциальных уравнений и их систем, а также проведение вычислительных экспериментов по решению практических задач.

2.ОСНОВЫ ТЕОРИИ

2.1. Физическая модель полета ЛА

Траектория полета ракеты представляет собой сложную кривую. Для упрощения расчетов не будем учитывать влияние кривизны и вращения Земли на движение ЛА, а также примем, что движение происходит без колебаний вокруг продольной оси ракеты. Траектория полета делится на два участка: активный (с работающим двигателем) и пассивный (с неработающим двигателем).

С учетом принятых допущений центр масс ракеты будет совершать поступательное движение под действием сил, действующих в одной плоскости: Р – силы тяги, Х – силы лобового сопротивления, G – силы тяжести. На рис. 1 показана система сил, приложенных к центру масс ракеты на траектории в произвольный момент времени.

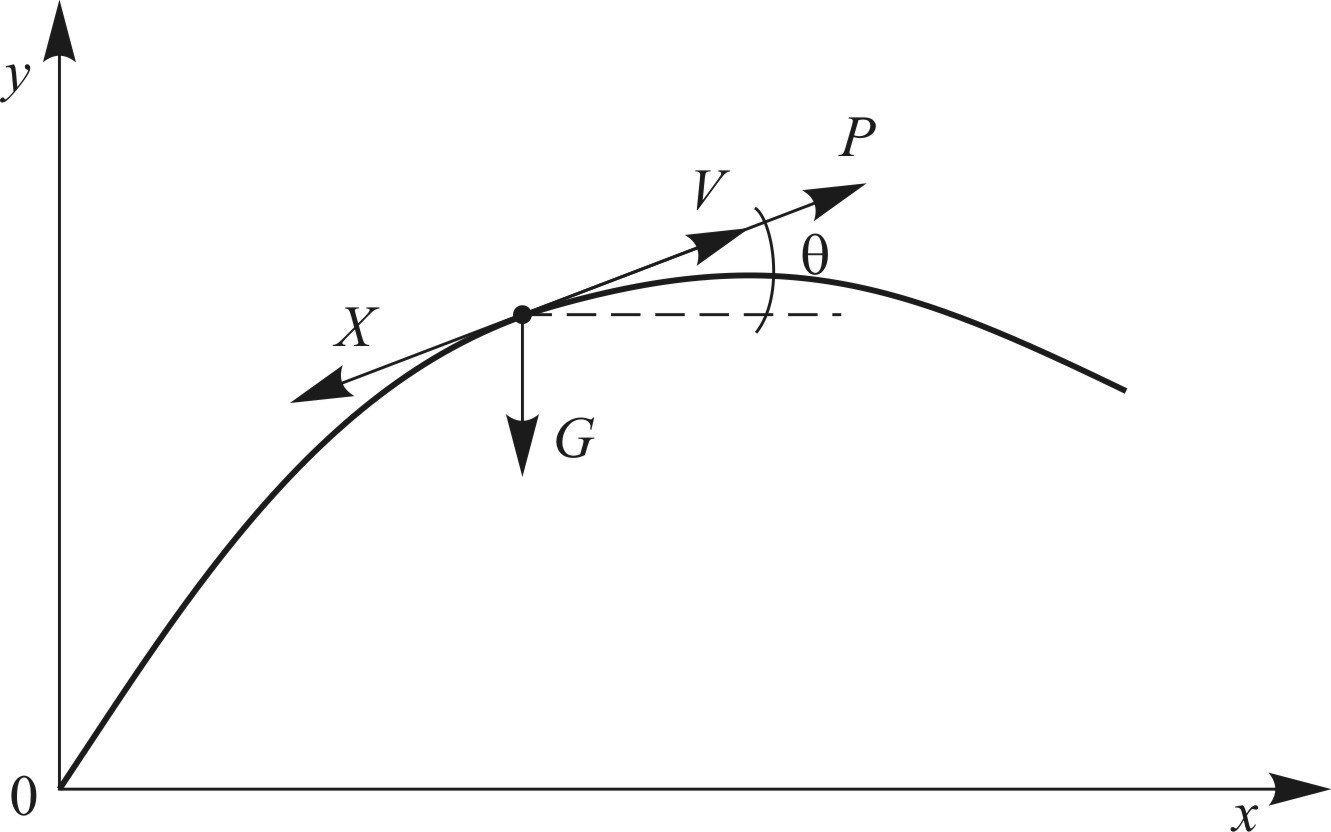Рис. 1. Схема сил, действующих на центр масс ЛА

ЛА запускается с земли (x₀,y₀)=(0,0) под углом θ=θ₀ к горизонту со скоростью V=V₀. Изменением ускорения свободного падения по высоте пренебрегаем (g=const), тягу принимаем постоянной в течение всего времени активного участка (t_a), расход массы определяется соотношением m_t /t_a, где m_t – масса топлива.

Методика расчета траектории базируется на основном законе механики (втором законе Ньютона), связывающем ускорение, испытываемое точкой массой m под действием силы F:

.

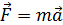Если на тело действует несколько сил, то 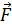– равнодействующая сила:

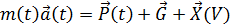
2.2. Математическая модель траектории полета ЛА

В соответствие с принятой физической моделью в основе математической модели, описывающей траекторию полета неуправляемого ЛА, лежит система уравнений, описывающих движение тела переменной массы, брошенного под углом к горизонту.

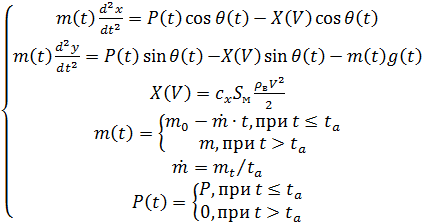(1)

где 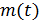– масса ЛА;

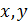– координаты центра масс ЛА на траектории;

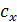– коэффициент аэродинамического сопротивления;

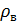– плотность воздуха;

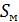– площадь миделя (площадь поперечного сечения ЛА);

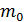– стартовая масса ЛА.

Дифференциальные уравнения второго порядка в рассмотренной системе (1) могут быть заменены на дифференциальные уравнения первого порядка, заменив 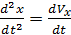и .

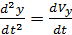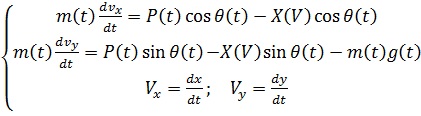(2)

2.3. Численная модель траектории полета ЛА

Полученную систему дифференциальных уравнений первого порядка c заданными начальными условиями можно решить различными способами.

Одним из наиболее распространенных методов решения обыкновенных дифференциальных уравнений является метод конечных разностей (МКР). Рассмотрим применение МКР для численного решения на ЭВМ простейшего дифференциального уравнения первого порядка:

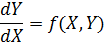
с начальными условиями X₀ , Y(X₀) = Y₀.

Решение будем искать в интервале [X₀ ,b] и будем полагать, что функция на данном интервале удовлетворяет условиям гладкости.

Разобьем область аргументаХ на множество отрезков длиной ΔX и разложим функцию Yв ряд Тейлора в окрестности произвольной точки X_i из области существования функции:

.
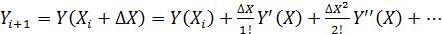Отбрасывая члены ряда, содержащие производные второго и высшего порядков, получаем конечно-разностное выражение первой производной

.

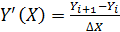Отсюда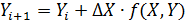

Вычисляя последовательно от начального значения Y₀ значения Y₁, Y₂, Y₃, ... по данной формуле, находим искомое решение.

На рис. 2 показана форма численного решения, получаемого с помощью таких вычислений

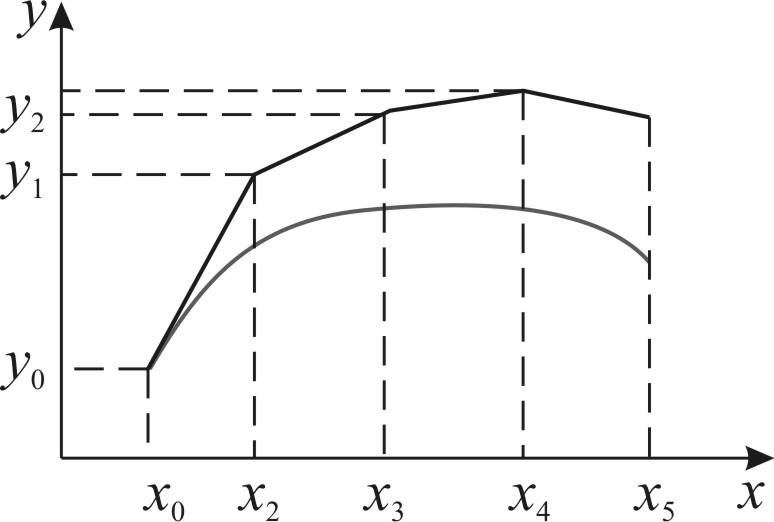
Рис.2. Схема приближенного решения методом Эйлера

Данный метод решения обыкновенного дифференциального уравнения носит название метода Эйлера. При достаточно малых величинах шага 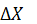. Метод Эйлера дает решение с большой точностью, так как погрешность близка к 0( 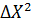) на каждом шаге процесса.

Для решения системы уравнений (2) методом Эйлера запишем ее в конечно-разностном виде:

,

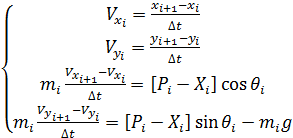где i – номер текущего шага по времени.

Выразим в этих уравнениях в явном виде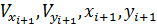

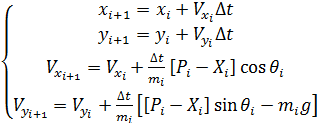. (3)

Решая систему уравнений (3) на каждом шаге по времени, можно последовательно вычислить все точки траектории полета ЛА.

ОСНОВНЫЕ ТРЕБОВАНИЯ К КУРСОВОЙ РАБОТЕ

Задание на курсовую работу

Студенту, выполняющему курсовую работу, формулируется задание разработать численную модель, алгоритм и программу расчета траектории полета ЛА с целью:

а) исследования влияния заданного параметра ЛА на дальность полета;

б) обеспечения определенной дальности полета ЛА варьированием заданного параметра ЛА.

Исходными данными для расчета являются:

угол бросания, время активного участка траектории, площадь миделя, коэффициент аэродинамического сопротивления, плотность воздуха, стартовая масса, конечная масса, начальная скорость, сила тяги. Для задачи б задается дополнительно дальность полета.

Варианты заданий представлены в приложении 1.

Содержание пояснительной записки

Пояснительная записка состоит из следующих разделов.

· Введение

· Постановка задачи

· Математическая постановка задачи

· Метод решения задачи

· Блок-схема программы

· Листинг программы

· Результаты расчета. Результаты расчета представляются в виде текстового файла с параметрами траектории и графиков траектории полета и зависимости дальности от исследуемого параметра (графики строятся в С++).

· Анализ результатов