Побудова результуючої системи лінійних алгебраїчних рівнянь
Підставляючи розклад (22) у слабку форму рівнянь Гальоркіна (24), отримаємо СЛАР відносно невідомих вузлових значень  , яка в матричній формі набуває вигляду
, яка в матричній формі набуває вигляду
 , (27)
, (27)
з коефіцієнтами
 ,
, 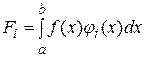 . (28)
. (28)
Матриця 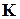 системи (27) називається матрицею жорсткості, а права частина
системи (27) називається матрицею жорсткості, а права частина  - вектором навантаження.
- вектором навантаження.
Враховуючи співвідношення (25), бачимо, що у виразі для коефіцієнтів матриці жорсткості (28) лише значення індекса  рівні
рівні 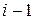 ,
, 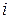 та
та 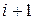 дають відмінні від нуля значення самих коефіцієнтів
дають відмінні від нуля значення самих коефіцієнтів 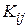 . Причому інтеграл
. Причому інтеграл 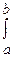 буде містити лише доданки
буде містити лише доданки  та
та 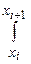 , що відповідають вкладам СЕ з номерами
, що відповідають вкладам СЕ з номерами 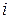 та
та 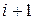 , відповідно. Це означає, по-перше, що матриця жорсткості
, відповідно. Це означає, по-перше, що матриця жорсткості 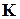 буде трьохдіагональною і симетричною, а, по-друге, що значення коефіцієнта
буде трьохдіагональною і симетричною, а, по-друге, що значення коефіцієнта  буде складатися з двох доданків: інтегралу
буде складатися з двох доданків: інтегралу  , який є внеском СЕ з номером
, який є внеском СЕ з номером 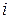 , та інтегралу
, та інтегралу 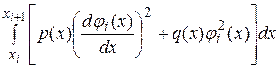 , який є внеском СЕ з номером
, який є внеском СЕ з номером 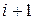 . Тому, на практиці, обчислення коефіцієнтів матриць СЛАР (27) здійснюють не безпосередньо за формулами (28), а шляхом обчислення локальних матриць жорсткості
. Тому, на практиці, обчислення коефіцієнтів матриць СЛАР (27) здійснюють не безпосередньо за формулами (28), а шляхом обчислення локальних матриць жорсткості  та вектора навантажень
та вектора навантажень 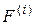 з наступним рознесенням їх у глобальні матрицю жорсткості
з наступним рознесенням їх у глобальні матрицю жорсткості 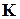 та вектор навантаження
та вектор навантаження  . Такий підхід до формування результуючої СЛАР в МСЕ у науковій літературі отримав назву ассемблювання.
. Такий підхід до формування результуючої СЛАР в МСЕ у науковій літературі отримав назву ассемблювання.
Отже, на кожному СЕ тепер потрібно обчислити локальну матрицю жорсткості  та вектор навантаження
та вектор навантаження 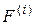 . Оскільки ми вибрали лінійні СЕ, тобто елементи з двома вузлами, і у кожному вузлі шукається лише одна невідома величина, то локальна матриця жорсткості
. Оскільки ми вибрали лінійні СЕ, тобто елементи з двома вузлами, і у кожному вузлі шукається лише одна невідома величина, то локальна матриця жорсткості  буде мати розмір
буде мати розмір 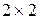 (і, відповідно, локальний вектор навантаження
(і, відповідно, локальний вектор навантаження 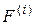 - розмір 2):
- розмір 2):
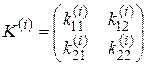 ,
, 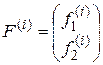 .
.
Тоді, враховуючи вище сказане і співвідношення (28), будемо мати, що
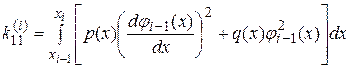 ,
,
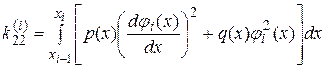 , (29)
, (29)
 ,
, 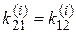 ,
,
та
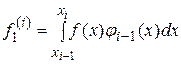 ,
, 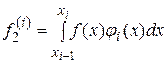 . (30)
. (30)
Схематично процес ассемблювання глобальної матриці жорсткості 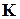 та вектора навантаження
та вектора навантаження  з локальних матриць
з локальних матриць  та вектора
та вектора 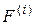 , відповідно, для тестової сітки з чотирьох СЕ, можна зобразити таким чином
, відповідно, для тестової сітки з чотирьох СЕ, можна зобразити таким чином
 , (31)
, (31)
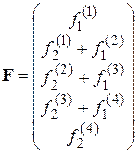 . (32)
. (32)
Отже, розв’язання крайової задачі (20)-(21) МСЕ з використанням одновимірних кусково-лінійних базисних функцій (25) для 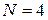 звелося до СЛАР (27) з матрицею виду (31) та правою частиною виду (32).
звелося до СЛАР (27) з матрицею виду (31) та правою частиною виду (32).
Програмна реалізація описаного вище процесу побудови локальних матриці жорсткості та вектора навантажень, і їх ассемблювання в середовищі MATHCAD наведена на рис. 3-4. Для обчислення локальних матриць жорсткості на елементі з номером 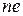 за формулами (29) введено функцію STIFF(ne). Оскільки базисні функції на першому та останньому СЕ визначаються окремо, то для обчислення локальних матриць жорсткості на цих елементах введено окремі функції STIFF_1 та STIFF_n, відповідно. Аналогічним чином організовано процес обчислення локальних векторів навантажень за формулами (30) за допомогою функцій LOAD(ne), LOAD_1 і LOAD_n.
за формулами (29) введено функцію STIFF(ne). Оскільки базисні функції на першому та останньому СЕ визначаються окремо, то для обчислення локальних матриць жорсткості на цих елементах введено окремі функції STIFF_1 та STIFF_n, відповідно. Аналогічним чином організовано процес обчислення локальних векторів навантажень за формулами (30) за допомогою функцій LOAD(ne), LOAD_1 і LOAD_n.
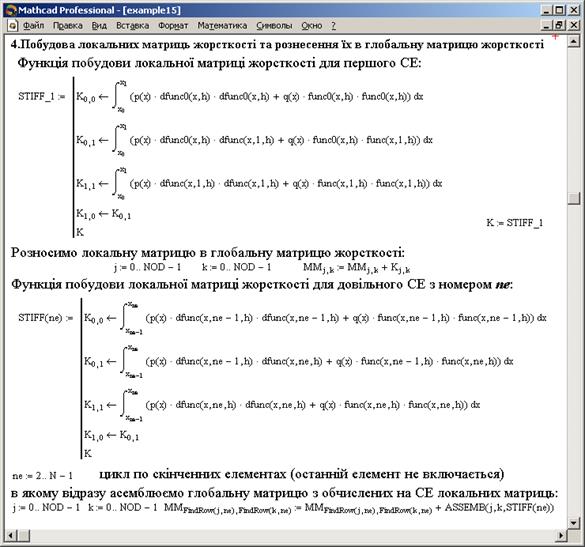
Рис.3. Побудова локальних матриць жорсткості та їх ассемблювання
Для рознесення локальних матриць у глобальні введено функцію FindRow(i,ne), яка дозволяє визначити номер рядка глобальної матриці жорсткості (вектора навантаження) для вузла з номером i на СЕ з номером ne,виду
 .
.
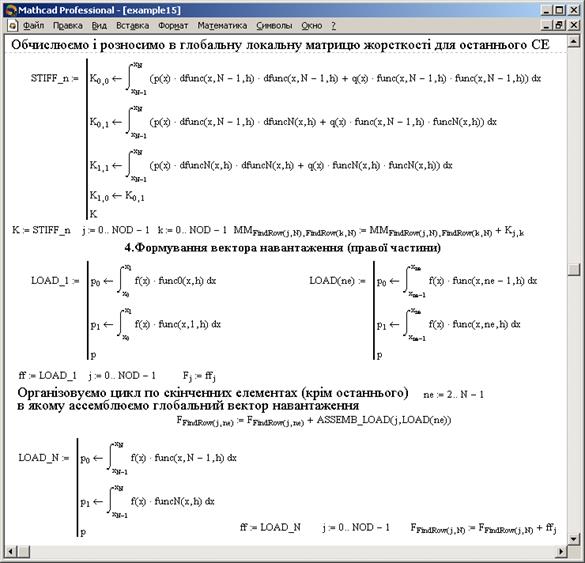
Рис.4. Побудова локальних векторів навантаження та їх ассемблювання
Також, тут використовуються функції
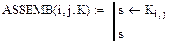 ,
, 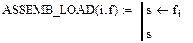 ,
,
які призначені для отримання конкретного елемента локальної матриці жорсткості та локального вектора навантаження, відповідно.
ВРАХУВАННЯ ГРАНИЧНИХ УМОВ
Розрізняють два типи граничних умов: головні граничні умови та природні граничні умови. Формальну ознаку поділу граничних умов на головні та природні можна сформулювати таким чином: якщо задано диференціальне рівняння порядку 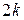 , то граничні умови, що містять похідні до порядку
, то граничні умови, що містять похідні до порядку  включно є головними, а граничні умови, що містять похідні порядку
включно є головними, а граничні умови, що містять похідні порядку 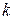 та вище називаються природними граничними умовами.
та вище називаються природними граничними умовами.
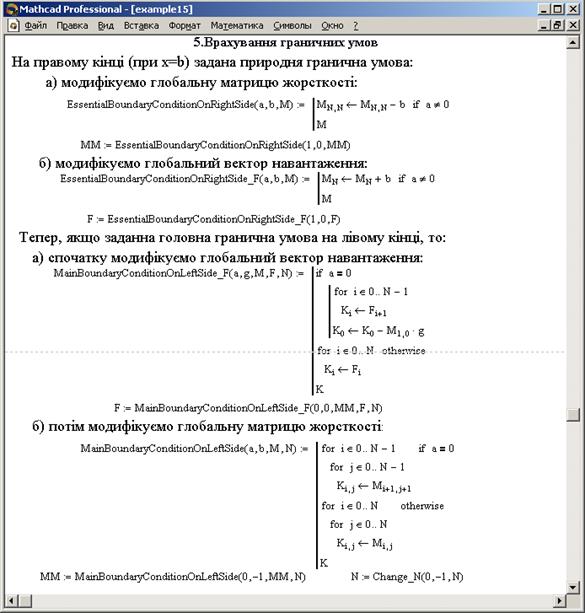
Рис.5. Врахування граничних умов
Врахування головної граничної умови на лівому(правому) кінці полягає в тому, що перший(останній) стовпець глобальної матриці жорсткості, який є стовпцем коефіцієнтів при відомому значенні, домножається на це значення і переноситься в праву частину системи, причому відкидається перша(остання) стрічка глобальної матриці жорсткості і перший (останній) елемент глобального вектора навантаження. Для цього (див. рис. 5) введено функцію модифікації глобального вектора навантаження 
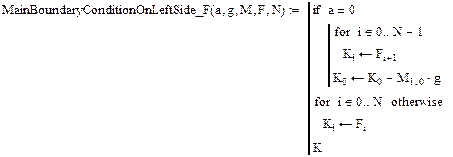
та функцію модифікації глобальної матриці жорсткості 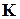
 .
.
Природня гранична умова на лівому(правому) кінці для рівняння (20) в загальному випадку має вигляд
 ,
,  . (33)
. (33)
Це означає, що, як наслідок інтегрування за частинами, у слабкій формі рівнянь Гальоркіна (24) з’явиться доданок 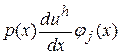 , який з врахуванням умови (33) можна перетворити до вигляду
, який з врахуванням умови (33) можна перетворити до вигляду 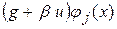 . Тоді, якщо
. Тоді, якщо  , то відповідне рівняння результуючої СЛАР (тобто перше рівняння, якщо природня умова (33) задана на лівому кінці при
, то відповідне рівняння результуючої СЛАР (тобто перше рівняння, якщо природня умова (33) задана на лівому кінці при 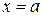 і останнє рівняння, якщо природня умова (33) задана на правому кінці при
і останнє рівняння, якщо природня умова (33) задана на правому кінці при 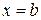 ) доповниться вільним членом
) доповниться вільним членом 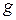 , який потрібно просто врахувати у векторі навантаження
, який потрібно просто врахувати у векторі навантаження  :
:
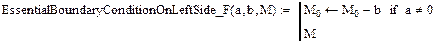 ,
,
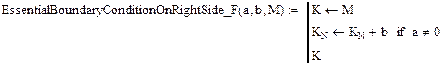 .
.
Якщо 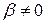 , то з’являється додатково доданок
, то з’являється додатково доданок 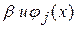 , який містить невідому функцію
, який містить невідому функцію 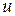 , тобто це означає, що потрібно модифікувати той елемент глобальної матриці жорсткості
, тобто це означає, що потрібно модифікувати той елемент глобальної матриці жорсткості 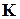 , який є коефіцієнтом при відповідному вузловому значення невідомої функції
, який є коефіцієнтом при відповідному вузловому значення невідомої функції 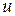 . Таким елементом є перший (останній) елемент на головній діагоналі, якщо природня умова (33) задана на лівому(правому) кінці. Реалізацію цього випадку задання природної граничної умови в середовищі MATHCAD можна здійснити, визначивши аналогічні функції
. Таким елементом є перший (останній) елемент на головній діагоналі, якщо природня умова (33) задана на лівому(правому) кінці. Реалізацію цього випадку задання природної граничної умови в середовищі MATHCAD можна здійснити, визначивши аналогічні функції
 ,
,
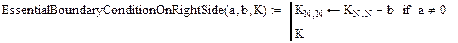 .
.
Тоді для врахування однорідної природної граничної умови (21), як видно з рис. 5, залишається здійснити такі виклики наведених вище функцій
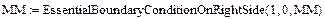 ,
, 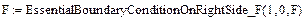 .
.
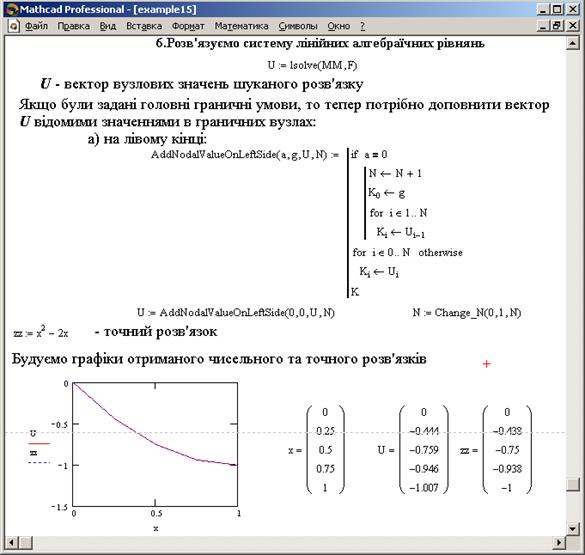
Рис.6. Розв’язання СЛАР та оцінка точності наближеного розв’язку
